Р исунок 22 – Положение прямой относительно плоскостей проекций

Прямые частного положения разделяются на проецирующие прямые (перпендикулярные плоскости проекций) и на прямые уровня (параллельные одной плоскости проекций).

Прямая общего положения называется восходящей, если её проекции ориентированы одинаково (прямая l на рисунке 23), и нисходящей, если её проекции ориентированы противоположно (прямая m на рисунке 23). У прямой l ближайшая к наблюдателю точка М (наблюдатель предполагается стоящим лицом к плоскости П₂) располагается ниже, чем более удалённая от наблюдателя точка N. Эта прямая по мере удаления от наблюдателя поднимается вверх (восходит). Прямая m по мере удаления от наблюдателя понижается (нисходит). Ориентация проекций восходящей прямой l и нисходящей прямой m обозначена стрелками.

Инцидентность (взаимопринадлежность) точки прямой. Следы прямой

Рисунок 23 – Комплексный чертёж прямых общего положения

Если точка принадлежит прямой в пространстве, то проекции этой точки принадлежат соответствующим проекциям данной прямой на комплексном чертеже (рисунок 23), прямая m и принадлежащие ей точки А,В). Как видно, А₁ m₁ и А₂ m₂ ; В₁ m₁ и В₂ m₂, следовательно, А m и В m.

Следом прямой на плоскости называется точка пересечения прямой с плоскостью. Точки пересечения прямой плоскостями проекций П₁ и П₂ будем называть соответственно горизонтальным и фронтальным следами данной прямой.

Положение прямой относительно плоскостей проекций

Как уже отмечалось, к прямым частного положения относятся прямые уровня, т.е. параллельные плоскости проекций (в соответствии с рисунком 22 это прямые h, f, p), и проецирующие прямые, т.е. перпендикулярные плоскости проекций (в соответствии с рисунком 22, прямые i, q, p’).

Прямая, параллельная горизонтальной плоскости проекций П₁, называется горизонталью и обозначается на чертеже через h. Так как все точки горизонтали имеют одну и ту же высоту, то её фронтальная проекция h₂ располагается на комплексном чертеже параллельно оси х₁₂, а на горизонтальную плоскость проекций данная прямая проецируется в натуральную величину в соответствии с рисунком 24. Также в натуральную величину на плоскость П₁ проецируется угол  наклона горизонтали h к фронтальной плоскости проекций П₂: А₁D₁=АD; (h₁ х₁₂)=.

Прямая, параллельная фронтальной плоскости проекций П₂, называется фронталью и обозначается на чертеже через f. Так как все точки фронтали имеют одну и ту же глубину, то её горизонтальная проекция f₁ располагается на комплексном чертеже параллельно оси х₁₂, а на фронтальную плоскость проекций данная прямая проецируется в натуральную величину (рисунок 24). Также в натуральную величину на плоскость П₂ проецируется угол  наклона фронтали к горизонтальной плоскости проекций П₁: E₂F₂=EF; (f₂ х₁₂)=.

Прямая, параллельная профильной плоскости проекций, называется профильной прямой и обозначается на чертеже через р. Так как все точки профильной прямой имеют одну и туже широту, то её горизонтальная р₁ и фронтальная р₂ проекции располагаются на комплексном чертеже перпендикулярно оси х₁₂ в соответствии с рисунком 24, а в натуральную величину данная прямая проецируется на профильную плоскость проекций П₃. На эту же плоскость проекций спроецируются в натуральную величину углы наклона профильной прямой р соответственно к плоскостям проекций П₁ и П₂. Следует заметить, что для определения профильной прямой необходимо задать на проекциях р₁ и р₂ прямой р проекции её двух точек, например В и С (рисунок 24). Для прямых h и f это делать совсем не обязательно. Обычно при решении различных вопросов с профильными прямыми прибегают к построению третьей проекции на профильную плоскость проекций П₃.

Рисунок 24 – Прямые уровня

Прямая i, перпендикулярная горизонтальной плоскости проекций П₁, называется горизонтально проецирующей прямой. Она проецирует все свои точки на плоскость П₁ в одну точку i₁, которая является её горизонтальной проекцией в соответствии с рисунком 25. Фронтальная проекция i₂ прямой i перпендикулярна оси х₁₂. Прямая i, будучи параллельной плоскости проекций П₂, проецируется на эту плоскость без искажения, т.е. АВ=А₂В₂. Точки А и В, как имеющие одну и ту же горизонтальную проекцию i₁A₁B₁, являются горизонтально конкурирующими.

Рисунок 25 – Проецирующие прямые

Аналогично, прямая q, перпендикулярная фронтальной плоскости проекций П₂, проецирует все свои точки, в том числе и точки С и D (рисунок 25) на плоскость проекций П₂ в одну точку: q₂С₂D₂. Эта прямая называется фронтально проецирующей прямой. Горизонтальная проекция q₁ прямой q перпендикулярна оси х₁₂. Прямая q, будучи параллельной плоскости проекций П₁, проецируется на неё без искажения, т.е. СD=C₁D₁. Точки С и D, как имеющие одну и ту же фронтальную проекцию q₂C₂D₂, являются фронтально конкурирующими.

Прямая р, перпендикулярная профильной плоскости проекций П₃, проецирует все свои точки в одну на эту плоскость проекций. Эта прямая называется профильно проецирующей прямой. Горизонтальная р₁ и фронтальная р₂ проекции прямой р параллельны оси х_12. Так как прямая р параллельна плоскостям проекций П₁ и П₂, то она проецируется на эти плоскости без искажения, т.е. р=р₁=р₂.

Взаимное положение двух прямых

Две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.

Если прямые а и b пересекаются в некоторой точке K, то на основании свойства принадлежности точки прямой линии проекции К₁ и К₂ точки К должны принадлежать одноименным проекциям прямых а и b в соответствии с рисунком 26.

Рисунок 26 – Взаимное положение двух прямых

Иначе говоря, точки пересечения одноименных проекций двух пересекающихся прямых лежат на одной и той же линии связи.

Если прямые с и d параллельны, то на основании свойства параллельности одноименные проекции параллельных прямых также параллельны, т.е. с₁Dd₁ и c₂Dd₂ в соответствии с рисунком 26.

Если прямые e и m скрещиваются и их одноименные проекции соответственно пересекаются в точках M₁N₁ и R₂S₂, то эти точки не должны лежать на одной линии связи (рисунок 26), так как в противном случае прямые e и m пересекались бы. Следует заметить, что точки М и N являются горизонтально конкурирующими, а точки R и S – фронтально конкурирующими.

Если прямые являются профильными, то для определения взаимного положения прямых необходимо построить профильные проекции этих прямых. Например, рассматривая двухкартинный комплексный чертёж (на П₂ и П₁) прямых АВ и СD (рисунок 27), можно ошибочно сделать заключение, что они параллельны. В действительности прямые скрещиваются, что очевидно после построения профильной проекции. В случае, когда только одна из прямых занимает профильное положение, для определения взаимного положения прямых кроме построения профильной проекции можно использовать метод пропорционального деления отрезка: если прямые пересекаются, то точка пересечения делит обе проекции профильного отрезка в одном и том же соотношении.

Рисунок 27 – Скрещивающиеся профильные прямые

Проекции прямого угла. Определение длины отрезка

Построение проекций прямого угла осуществляется в соответствии со следующей теоремой:

Для того чтобы прямой угол проецировался ортогонально в виде прямого угла, необходимо и достаточно, чтобы одна его сторона была параллельна плоскости проекций, а вторая сторона не перпендикулярна к ней, т.е. одна сторона прямого угла должна быть линией уровня (рисунок 28)

Рисунок 28 - Проецирование прямого угла

Применительно к комплексному чертежу (рисунок 29).

Рисунок 29- Проекции прямого угла на соответствующих плоскостях

проекций

Проекция отрезка на некоторую плоскость проекций связана с проецируемым отрезком равенством: а' = а∙cos α.

Рисунок 30- Проекция отрезка на плоскость проекций

Согласно рисунку 30 натуральная величина отрезка равна длине гипотенузы прямоугольного треугольника, одним катетом которого является проекция данного отрезка на данную плоскость проекций, а величина второго катета определяется как разность расстояний концов данного отрезка от данной плоскости проекций (рисунок 30).

Лекции 2.2

Изображение плоскости на комплексном чертеже

Плоскость можно задать:

- тремя точками, не лежащими на одной прямой;

- прямой и точкой, не лежащей на этой прямой;

- двумя пересекающимися прямыми;

- двумя параллельными прямыми;

- отсеком.

Наиболее наглядным является задание плоскости отсеком. Простейшим из отсеков является треугольник.

Рисунок 31 – Положение плоскости относительно плоскостей

проекций

Как и в случае с прямыми линиями различают плоскости общего и частного положения. Плоскости, наклонённые ко всем плоскостям проекций, называются плоскостями общего положения (например, плоскость  на рисунке 31). Плоскости, перпендикулярные либо параллельные плоскости проекций, называются плоскостями частного положения (в соответствии с рисунком 31 это плоскости , , , Г, Ф, Р).

По аналогии с прямыми линиями плоскости частного положения разделяются на проецирующие плоскости, т.е. перпендикулярные плоскости проекций (плоскости , ,  на рисунке 31) и плоскости уровня – параллельные плоскости проекций (плоскости Г, Ф, Р).

Плоскость общего положения, как и прямая общего положения, может быть восходящей и нисходящей. На комплексном чертеже проекции восходящей плоскости ориентированы одинаково, а нисходящей – противоположно. Изображение нисходящей плоскости соответствует рисунку 32.

Инцидентность (взаимопринадлежность) точки прямой, плоскости

Если точка принадлежит плоскости в пространстве, то проекции этой точки принадлежат соответствующим проекциям какой-либо прямой, лежащей в данной плоскости (в соответствии с рисунком 32 прямая АВ и принадлежащая ей точка 1; прямая ВС и принадлежащая ей точка 2). В данном примере и точка М принадлежит плоскости треугольника АВС, т.к. точка М расположена на прямой А-2, лежащей в плоскости треугольника. При этом следует отметить, что плоскость безгранична, поэтому некоторые построения могут выходить за пределы треугольника.

Прямая А-2 является фронталью плоскости треугольника АВС (горизонтальная проекция этой прямой А₁2₁Dвоображаемой оси проекций х₁₂). Точка К принадлежит данной фронтали (К₁f₁ и К₂f₂) и, следовательно, принадлежит плоскости треугольника АВС. Как видно, точка К принадлежит и прямой С-1 данного треугольника. Эта прямая является горизонталью (фронтальная проекция прямой С₂1₂Dвоображаемой оси х₁₂).

Рисунок 32 – Принадлежность точки плоскости

Очевидно, через каждую точку плоскости можно провести одну горизонталь и одну фронталь, лежащие в этой плоскости в соответствии с рисунком 29.

Следы плоскости

Следом плоскости называется прямая её пересечения с плоскостью проекций. На рисунке 33 плоскость  задана следами l и m: l=∩П₂ и m=∩П₁, а М=∩х₁₂ – точка пересечения плоскости  с осью проекций х₁₂.

Точка М, принадлежащая одновременно обеим плоскостям проекций, должна, очевидно, лежать на обоих следах плоскости . Следовательно, следы плоскости  пересекаются на оси: m∩l=М, Мх₁₂. Для задания плоскости следами достаточно дать горизонтальную проекцию горизонтального следа и фронтальную проекцию фронтального следа, так как другие проекции следов совпадают с осью х₁₂ в соответствии с рисунком 33.

Нетрудно видеть, след на горизонтальной плоскости проекций П₁ является не чем иным, как горизонталью h данной плоскости, а след на фронтальной плоскости проекций П₂ является её фронталью f. Задание плоскости её следами на плоскостях проекций является частным случаем задания плоскости двумя пересекающимися прямыми, а именно пересекающимися прямыми уровня.

Рисунок 33 – Следы плоскости

Положение плоскости относительно плоскостей проекций

Выше было отмечено, что к плоскостям частного положения относятся плоскости уровня (параллельные плоскости проекций) и плоскости проецирующие (перпендикулярные плоскости проекций). В первом случае это плоскости Г, Ф, Р в соответствии с рисунком 31, во втором случае это плоскость .

Все точки плоскостей уровня одинаково удалены от соответствующих плоскостей проекций.

На рисунке 34 представлены примеры задания плоскостей уровня. Плоскость Г, параллельную горизонтальной плоскости проекций, называют горизонтальной плоскостью уровня, плоскость Ф, параллельную фронтальной плоскости проекций – фронтальной плоскостью уровня, а плоскость Р – профильной плоскостью уровня (она параллельна профильной плоскости проекций).

Рисунок 34 – Плоскости уровня

Каждая плоскость уровня, будучи параллельной соответствующей плоскости проекций, в то же время перпендикулярна двум другим плоскостям проекций. Так, горизонтальная плоскость Г, параллельная плоскости проекций П₁, перпендикулярна фронтальной П₂ и профильной П₃ плоскостям проекций. Аналогично можно рассмотреть положение фронтальной Ф и профильной Р плоскостей уровня. Поэтому плоскости уровня на комплексном чертеже могут быть заданы одной проекцией, как, например, горизонтальная плоскость уровня Г своей фронтальной проекцией Г₂ и фронтальная плоскость уровня Ф своей горизонтальной проекцией Ф₁, или двумя проекциями, как профильная плоскость уровня Р своими фронтальной Р₂ и горизонтальной Р₁ проекциями. Каждая из этих проекций является прямой, параллельной или перпендикулярной оси проекций х₁₂, и одновременно соответствующим следом каждой из рассматриваемых плоскостей. Так, Г₂ есть фронтальный след горизонтальной плоскости уровня Г. Горизонтальная проекция этой плоскости занимает всё поле проекций плоскости П₁. Как уже было сказано, аналогично можно рассмотреть положение фронтальной Ф и профильной Р плоскостей уровня.

Любой геометрический объект, лежащий в соответствующей плоскости уровня, проецируется без искажения на плоскости проекций П₁, П₂, П₃.

На рисунке 35 представлены примеры задания проецирующих плоскостей.

Плоскость , перпендикулярная к плоскости проекций П₁, называется горизонтально проецирующей плоскостью. Эта плоскость проецирует все свои точки на горизонтальную плоскость проекций в одну прямую ₁, которая является горизонтальной проекцией плоскости  и одновременно её горизонтальным следом. Две другие проекции этой плоскости (фронтальная и профильная) занимают соответственно всё поле проекций плоскостей П₂ и П₃.

Рисунок 35 – Проецирующие плоскости

Горизонтальная проекция точки или плоской фигуры, лежащих в горизонтально проецирующей плоскости , например, треугольника АВС, располагается на прямой ₁. В связи с этим можно сказать, что проекция ₁ и одновременно горизонтальный след горизонтально проецирующей плоскости  собирает на себе проекции точек, прямых и плоских фигур, расположенных в этой плоскости. Следует отметить, что горизонтально проецирующая плоскость  вполне определяется её одной проекцией ₁, а угол  измеряет угол наклона плоскости  к плоскости проекций П₂.

Плоскость , перпендикулярная к плоскости проекций П₂, называется фронтально проецирующей плоскостью. Эта плоскость проецирует все свои точки на фронтальной плоскости проекций в одну прямую ₂, которая является фронтальной проекцией плоскости  и одновременно её фронтальным следом (₁ есть горизонтальный след данной плоскости). Угол  измеряет угол наклона плоскости  к плоскости проекций П₂. Горизонтальная и профильная проекции фронтально проецирующей плоскости  занимают соответственно всё поле проекций плоскостей П₁ и П₃. Проекция ₂ плоскости  собирает на себе проекции точек, прямых, плоских фигур, расположенных в этой плоскости.

Плоскость Р, перпендикулярная к плоскости проекций П₃, называется профильно проецирующей плоскостью. Эта плоскость проецирует все свои точки на профильную плоскость проекций в одну прямую Р₃, которая является профильной проекцией плоскости Р и одновременно её профильным следом. Р₂ и Р₁ есть соответственно фронтальный и горизонтальный следы данной профильно-проецирующей плоскости. Горизонтальная и фронтальная проекции этой плоскости занимают соответственно всё поле плоскостей проекций П₁ и П₂. Проекция Р₃ плоскости Р собирает на себе проекции точек, прямых и плоских фигур, расположенных в данной плоскости.

Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Так, прямая l параллельна прямой b, расположенной в плоскости  в соответствии с рисунком 36, следовательно,

l// (прямая l параллельна плоскости ).

На комплексном чертеже это условие обеспечивается параллельностью соответствующих проекций прямой l и прямой b в соответствии с рисунком 2.13. Так, l₁//b₁ и l₂//b₂, следовательно, l//.

Рисунок 36 – Параллельность прямой и плоскости

Рисунок 37 – Комплексный чертёж параллельных прямой и плоскости

Параллельность плоскостей

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Так, пересекающиеся прямые с и d плоскости  (рисунок 38 а) параллельны пересекающимся прямым с’ и d’ плоскости , следовательно, плоскость  параллельна плоскости  (//).

Рисунок 38 – Параллельность плоскостей

На комплексном чертеже это условие обеспечивается параллельностью соответствующих проекций прямых с и d плоскости  и прямых с и d плоскости . Так, с//с’ и d//d’, следовательно, // в соответствии с рисунком 38 б.

Пересечение прямой линии с плоскостью

Это есть позиционная задача, т.к. в ней определяется общий элемент данных геометрических объектов, т.е. их точка пересечения, что соответствует рисунку 39.

Алгоритм решения задачи основывается на следующем способе:

1)через прямую линию проводят вспомогательную плоскость-посредник;

2)находят линию пересечения вспомогательной плоскости с данной плоскостью;

3)отмечают точку пересечения полученной линии с данной линией;

4)определяют видимость данной прямой относительно данной плоскости.

Через прямую а, которая пересекает плоскость общего положения, заданную треугольником АВС, в соответствии с рисунком 39 проведена вспомогательная фронтально проецирующая плоскость (₂), обозначенная на чертеже ₂а₂.

Линией пересечения b плоскости  с заданной плоскостью треугольника АВС является прямая линия. Эта линия строится с помощью точек 1 и 2. Первоначально отмечаем фронтальные проекции 1₂ и 2₂ этих точек в пересечении следа ₂ плоскости с фронтальными проекциями А₂В₂ и А₂С₂ соответствующих сторон треугольника АВС. Затем по свойству принадлежности определяем горизонтальные проекции точек 1 и 2 на горизонтальных проекциях этих сторон.

Пересечение линии b₁ c линией a₁ определяет горизонтальную проекцию К₁ искомой точки К. Фронтальная проекция К₂ точки К получается в пересечении линии связи, проведённой из точки К₁ с линией a_2.

Видимость прямой а относительно плоскости треугольника АВС определена с помощью конкурирующих точек 1, 1 и 3, 3.

Рисунок 39 – Пересечение прямой линии с плоскостью

Пересечение двух плоскостей

В этой позиционной задаче общим элементом данных геометрических объектов является прямая линия. Её можно построить двумя способами: с помощью плоскостей-посредников частного положения, одновременно пересекающих обе данные плоскости и способом на основе пересечения прямой линии с плоскостью.

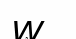Пример построения линии пересечения двух плоскостей способом секущих плоскостей-посредников представлен на рисунке 40.

Рисунок 40 – Пересечение двух плоскостей общего положения

Плоскость  определяется пересекающимися прямыми а и b, а плоскость  - параллельными прямыми с и d.

Для нахождения линии l пересечения плоскостей  и  проведём две фронтально проецирующие плоскости (₂) и (₂), являющиеся посредниками. Плоскость  пересекает данные плоскости  и  по прямым линиям 1-2(1₂-2₂, 1₁-2₁) и 3-4(3₂-4₂, 3₁-4₁). Точку пересечения этих прямых обозначим через К(К₁, К₂). Точка К принадлежит одновременно трём плоскостям , , . Следовательно, точка К принадлежит линии пересечения плоскостей  и . Плоскость  пересекает плоскости  и  по прямым линиям 5-6(5₁-6₁, 5₂-6₂) и 7-8(7₁-8₁, 7₂-8₂). Точкой пересечения этих линий является точка К. Она, как и точка К принадлежит линии пересечения плоскостей  и . Следовательно, прямая l, проходящая через точки К и К, есть искомая прямая пересечения данных плоскостей  и .

На рисунке 41 представлен пример построения линии пересечения двух плоскостей способом пересечения прямой линии с плоскостью. Плоскости заданы треугольниками АВС и EGF. Вспомогательные секущие плоскости (₂) и (₂) проведены через стороны EG и ВС треугольников. Плоскость (₂) пересекает треугольник АВС по прямой 1-2. Точка К является результатом пересечения прямых EG и 1-2. Плоскость (₂) пересекает треугольник EGF по прямой 3-4. Точка К является результатом пересечения прямых ВС и 3-4.

Рисунок 41 – Пересечение двух плоскостей общего положения

Точки К и К ограничивают отрезок искомой линии пересечения, находящийся в пределах обоих треугольников.

Относительная видимость треугольников определена на фронтальной проекции с помощью конкурирующих точек 2 и 4, из которых точка 4 стороны EG закрывает собой точку 2 стороны ВС. Видимость на горизонтальной плоскости проекций определена с помощью конкурирующих точек 5 и 6, из которых точка 6 стороны EG закрывает собой точку 5 стороны АС.

Лекция 2.3

Кривые линии

Кривую линию можно рассматривать как след движущейся точки. Эта точка может быть отдельной точкой или точкой, принадлежащей движущейся в пространстве линии или поверхности.

Кривые линии могут быть образованы пересечением кривой поверхности плоскостью (в общем случае), взаимным пересечением двух поверхностей, из которых хотя бы одна является кривой.

Законом образования кривой линии называется совокупность условий, определяющих эту линию. Точка, линия, поверхность перемещаются в пространстве, подчиняясь разным условиям. Плоскость может пересекать разнообразные кривые поверхности по самым различным направлениям. Взаимно пересекаться могут самые разнообразные поверхности при различном положении их относительно друг друга. Отсюда следует, что образование кривой линии может подчиняться бесчисленному множеству условий и может быть образовано бесчисленное множество кривых линий. Кроме того, одна и та же кривая линия может быть образована различными способами.

Например, эллипс может быть образован движением точки в плоскости, при котором в каждый данный момент сумма расстояний от этой точки до двух других неподвижных точек – фокусов эллипса – постоянна и равна большой оси эллипса. Но эллипс может быть образован и пересечением кругового цилиндра с плоскостью, расположенной произвольно по отношению к его оси или полным пересечением поверхностей двух круговых цилиндров одинакового диаметра.

Все кривые линии по положению их точек в пространстве делятся на два вида: плоские кривые – кривые, все точки которых лежат в одной плоскости (например, окружность, эллипс, парабола и т.д.) и пространственные кривые – кривые, точки которых не лежат в одной плоскости, например, винтовая линия

Проекционные свойства плоских кривых

Допустим, что данная кривая l лежит в некоторой плоскости . Спроецируем кривую l на плоскость проекций П по направлению s в соответствии с рисунком 42. Тогда каждая точка М кривой l будет проецироваться в точку М плоскости П. В результате на плоскости П получится кривая l – проекция данной кривой l.

Рисунок 42 – Проекционные свойства плоских кривых

Кривая l будет обладать теми свойствами оригинала - кривой l, которые сохраняются при параллельном проецировании.

Рассмотрим основные свойства проекций плоских кривых линий.

Порядок плоской алгебраической кривой при параллельном проецировании не изменяется.

Проведём секущую m кривой l, лежащей в плоскости . Тогда в проекции получим прямую m, а точки пересечения линий m и l спроецируются в точки пересечения проекций m и l в соответствии с рисунком 42.

Таким образом, число точек пересечения линий m и l будет равно числу точек пересечения их проекций m и l, т.е. порядок проекции l будет равен порядку кривой l.

Бесконечно удалённые точки кривой проецируются в бесконечно удалённые точки её проекции.

При перемещении некоторой точки М по кривой l её проекция М будет перемещаться по кривой l. При удалении точки М в бесконечность в соответствии с рисунком 42 её проекция также станет бесконечно удалённой точкой.

Касательная к кривой проецируется в касательную к её проекции.

Точка А есть проекция точки А. Прямая t является проекцией прямой t, касательной к кривой l в точке А.

Число точек пересечения плоских кривых сохраняется при проецировании.

Плоские кривые в частном случае (когда направление проецирования параллельно плоскости кривой) могут проецироваться в прямые линии, а в случае параллельности плоскости кривой и плоскости проекций соответствующая проекция кривой будет конгруэнтна самой кривой.

Ортогональная проекция окружности

Как известно, параллельной проекцией окружности является кривая, называемая эллипсом. Поскольку ортогональная проекция является частным случаем параллельной, то очевидно, что ортогональной проекцией окружности будет тоже эллипс. Так, проецируя окружность, расположенную в плоскости  с центром в точке D, ортогонально на плоскость П, получим эллипс с центром в точке D в соответствии с рисунком 40.

Рассмотрим в окружности два взаимно перпендикулярных диаметра AB и CD, причём АВ проходит по прямой уровня плоскости  (по прямой h), т.е. АВ//П. Следовательно, АВ=АВ=d, где d – диаметр окружности. Диаметр CD как перпендикулярный к АВ, являющийся линией уровня плоскости , называется также линией наибольшего наклона данной плоскости к плоскости проекций П. Такое название объясняется тем, что среди различных прямых плоскости  линия наибольшего наклона CD, перпендикулярная к линии уровня АВ, образует наибольший угол с плоскостью проекций П.

Рисунок 43 – Ортогональная проекция окружности

Угол , образованный диаметром окружности CD и диаметром эллипса CD как проекцией CD, является линейным углом двугранного угла наклона плоскости  к плоскости П. Тогда CD=CD·cos, но CD=АВ=d, следовательно CD=d·cos. Как известно, взаимно перпендикулярные диаметры окружности обладают свойством сопряжённости (каждый сопряжённый диаметр делит пополам хорды, параллельные другому диаметру), это свойство при параллельном проецировании сохраняется, следовательно, диаметры АВ и CD будут сопряжёнными диаметрами эллипса. Но с другой стороны, эти диаметры взаимно перпендикулярны, так как являются проекциями взаимно перпендикулярных диаметров, один из которых параллелен плоскости проекций, поэтому они являются осями эллипса, причём АВ – большая ось, CD – малая ось.

Если провести какую-нибудь прямую n, перпендикулярную к плоскости  в соответствии с рисунком 2.19, то такая прямая будет перпендикулярна ко всякой прямой плоскости , в частности, будет перпендикулярна к диаметру АВ//П. Поэтому её ортогональная проекция n на плоскость П окажется прямой, перпендикулярной к проекции АВ диаметра АВ. Иначе говоря, проекция прямой, перпендикулярной к плоскости , параллельна малой оси эллипса.

Таким образом, большая ось эллипса, являющегося ортогональной проекцией окружности, плоскость  которой составляет угол  с плоскостью проекций, параллельна проекции линии уровня плоскости  и равна диаметру окружности, а малая ось параллельна проекции перпендикуляра к плоскости  и равна d·cos.

Рассмотрим соотношение осей полученного эллипса:

Для данных плоскостей  и П угол  и cos - величины постоянные. Вследствие этого cos может служить характеристикой отношения осей эллипса, которое, в свою очередь, характеризует форму эллипса.

Итак, как бы ни была расположена окружность в плоскости , на плоскости проекций всегда будет получаться эллипс одной и той же формы. Следует отметить, что при данном угле  не только форма эллипса будет постоянной, но и расположение осей также не будет зависеть от размеров и положения окружности в плоскости .

Если угол  увеличивать, то эллипс, имея постоянной большую ось, будет становиться всё уже. В пределе, когда угол  станет равным 90, а cos=0, т.е. плоскость  плоскости П, окружность будет проецироваться в отрезок.

Если cos=1, то плоскость  параллельна плоскости проекций и эллипс-проекция принимает форму окружности.

Рассмотрим построение окружности, расположенной в проецирующей плоскости в соответствии с рисунком 44, а.

Пусть окружность с центром в точке О и радиусом R лежит во фронтально проецирующей плоскости (₂).

Рисунок 44 ­­- Окружность в проецирующей плоскости

Выберем два взаимно перпендикулярных диаметра окружности АВ и CD, из которых АВ//П₂, а CD//П₁. Таким образом, диаметр CD совпадает с горизонталью плоскости , а АВ – с линией наибольшего наклона к плоскости П₁.

Тогда проекциями диаметра АВ будут служить отрезки А₁В₁ и А₂В₂=АВ=2R, диаметр CD спроецируется на П₂ в точку С₂D₂=0, а на плоскость П₁ в отрезок С₁D₁=CD=2R.

Таким образом в данном случае фронтальной проекцией окружности является отрезок прямой длиной 2R, горизонтальной проекцией – эллипс,

большой осью которого служит отрезок С₁D₁, малой осью – отрезок А₁В₁. Заметим, что малая ось А₁В₁ эллипса совпадает с проекцией n₁ перпендикуляра n к плоскости . Промежуточные точки эллипса можно построить при помощи двух концентрических окружностей, проведённых на осях С₁D₁ и А₁В₁ как на диаметрах.

Аналогично строят проекции окружности, расположенной в горизонтально проецирующей плоскости (₁), в соответствии с рисунком 44, б.

Поверхности. Образование и задание, определитель, каркас, очерк

Начертательная геометрия пользуется преимущественно кинематическим способом образования поверхностей. Это означает, что поверхность образуется непрерывным перемещением линии (образующей) в пространстве по определённому закону. Тогда и сама поверхность будет непрерывной. Образующая может или сохранять свою форму при изменении положения, или непрерывно изменять и форму, и положение в пространстве.

Принадлежность поверхности некоторому классу описывается такими элементами, которые однозначно определяют её форму и размеры.

Совокупность элементов поверхности (параметров), выделяющих данную поверхность из всего класса поверхностей, к которому она принадлежит, будем называть определителем поверхности.

Например, конус вращения полностью задаётся осью и образующей в соответствии с рисунком 45. Поэтому определитель конической поверхности  будет записан так: (i,l).

Задание оси i и образующей l конуса вращения позволяет построить этот конус. На нём можно провести любую другую прямолинейную образующую (l¹,l²,…) или окружность (q,m) поверхности, а также отметить произвольную её точку (М). Заметим, что этот способ задания конуса не является единственным.

Исходя из определителя поверхности конуса вращения, для задания конуса на чертеже достаточно задать проекции элементов определителя: i(l₁,i₂) и l(l₁,l₂) в соответствии с рисунком 46. Такой способ графического задания поверхности является метрически определённым и позволяет решать любые задачи на поверхности, а также её реконструировать.

Рисунок 45 – Конус вращении

Закон перемещения в пространстве кривой (образующей), описывающий поверхность, удобно задавать некоторыми неподвижными кривыми, по которым скользит движущаяся образующая. Эти кривые, называемые направляющими линиями, часто входят в состав определителя поверхности.

Таким образом, на любой кинематической поверхности можно выделить два семейства кривых линий: семейство образующих (l) и семейство направляющих (m), каждое из которых покрывает всю поверхность и состоит из каких-либо линий (плоских или пространственных) в соответствии с рисунком 47.

Если поменять местами образующие и направляющие, т.е. принять m за образующие, а l – за направляющие, то в результате получится та же поверхность .

Из кривых l¹,l²… и m¹,m²…, принадлежащих к указанным двум семействам линий, может быть составлен каркас кинематической поверхности.

Если учесть непрерывность перемещения образующей, а, следовательно, и непрерывность самой поверхности, то можно сделать очень важный для теории кинематических поверхностей вывод о том, что через любую точку поверхности можно провести пару кривых, принадлежащих двум различным семействам линий на поверхности.

Простейшей и основной задачей, входящей в виде элемента в решение любой более сложной задачи, является построение проекций точки, принадлежащей поверхности.

Р исунок 46 – Задание конуса вращения элементами определителя

Рисунок 47 – Каркас поверхности

Общий метод заключается в том, что для построения второй проекции, например, М₂ точки М, лежащей на поверхности и заданной проекцией М₁, проводят через эту проекцию точки М линию l(l₁), принадлежащую одному из семейств линий на поверхности. Затем строят вторую проекцию l₂ этой линии и проводят через точку М₁ линию связи. Вторая проекция М₂ точки М будет лежать в пересечении проведённой линии связи с линией l₂. Выбор линии того или другого семейства основывается на графической простоте этой линии. На рисунке 46 использована прямолинейная образующая l.

Задание на чертеже кинематических поверхностей, определяемых несколькими точками или линиями, сводится к заданию проекций этих точек и линий. При этом надо иметь в виду некоторые условия, дополняющие чертёж.

Рассмотрим, например, образование поверхности цилиндра вращения. Определитель этой поверхности  в соответствии с рисунком 48, а состоит из оси i(i₁,i₂) и образующей l(l₁,l₂): (i,l).

Цилиндр может быть образован также вращением кривой b, лежащей на его поверхности, или поступательным перемещением окружности m: m¹,m²,m³…(поверхность переноса). В этих случаях определитель должен быть обозначен: (i,b), (i,m).

Кинематическая поверхность может быть образована также движением образующей поверхности, а не линии, как это было до сих пор. При этом движущаяся поверхность образует множество поверхностей, называемое семейством.

Из дифференциальной геометрии известно, что поверхность, касающаяся в каждой своей точке некоторой поверхности данного семейства, называется огибающей данного семейства.

Так, цилиндр вращения может быть образован как огибающая однопараметрического семейства сфер (¹, ², ³…) с центрами О¹, О², О³…, расположенными на прямой i – оси цилиндра (рисунок 48, б).

Рисунок 48 – Способы образования цилиндра вращения

Этот цилиндр будет касаться сфер по окружностям больших кругов (m¹,m²,m²…), называемых характеристиками. Определитель поверхности

(i, R_), где R_ - радиус образующей сферы.

На практике из всех возможных способов образования поверхности и вида образующих линий выбирают наиболее простые и удобные для решения задач.

Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов её определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Поэтому для увеличения наглядности изображения поверхности во многих случаях указывают на чертеже наряду с проекциями определяющих поверхность точек и линий также и очертание поверхности на плоскостях проекций.

Предположим, что некоторая произвольная поверхность  проецируется на плоскость проекций П в соответствии с рисунком 49. Тогда можно выделить те проецирующие лучи, которые будут касаться поверхности  и образовывать некоторую проецирующую цилиндрическую поверхность.

Линия l касания проецирующей поверхности и заданной называется контурной линией. Линия l пересечения проецирующей поверхности с

плоскостью П называется очертанием данной поверхности .

Очертание поверхности получается, таким образом, как проекция контурной линии на данную плоскость проекций.

Очертание поверхности является границей видимости частей поверхности на данной плоскости. Оно отделяет область расположения проекций точек поверхности от всех других точек плоскости проекций. Поэтому при изображении поверхности на комплексном чертеже проекцию контурной линии на других плоскостях будем называть линией видимости.

Рисунок 49 – Очертание поверхности

На рисунке 50 изображена в двух проекциях сфера, очертания которой на плоскостях проекций П₁ и П₂ есть окружности q₁ и m₂. На другие плоскости проекций эти окружности проецируются в виде линий видимости q₂ и m₁ соответственно.

Рисунок 50 – Очертания и линии видимости сферы

На практике в различных областях техники получили широкое распространение следующие классы кинематических поверхностей:

1)поверхности вращения, которые образуются вращением произвольной образующей вокруг неподвижной оси, в частности, поверхности вращения второго порядка;

2)поверхности второго порядка общего вида;

3)линейчатые поверхности, которые могут быть образованы движением прямолинейной образующей;

4)винтовые поверхности, образуемые винтовым движением произвольной образующей, и, в частности, линейчатые винтовые поверхности – геликоиды;

5)циклические поверхности, которые могут быть образованы движением окружности постоянного или переменного диаметра.

Следует отметить, что отдельные поверхности могут быть отнесены не к одному, а к нескольким классам.

Линейчатые поверхности

Линейчатой поверхностью называется поверхность, которая может быть образована движением прямой линии в пространстве. В зависимости от характера движения образующей получаются различные типы линейчатых поверхностей.

Если прямолинейная образующая при своём движении перемещается по ломаной направляющей, то такая поверхность является гранной. При этом, если прямолинейная образующая во всех положениях проходит через неподвижную точку S (вершину), то полученная поверхность является пирамидальной в соответствии с рисунком 51, а. Определитель этой поверхности (l,m,S). Если прямолинейная образующая при своём перемещении имеет постоянное направление, то такая поверхность называется призматической в соответствии с рисунком 51, б. Определитель данной поверхности (l,m,s).

Рисунок 51 – Линейчатые гранные поверхности

Многогранники (пирамиды, призмы) – это замкнутые поверхности, образованные некоторым количеством граней. В данном случае и поверхность, и тело, ограниченное этой поверхностью, носят одно название. Элементами многогранника являются вершины, рёбра и грани; совокупность всех рёбер многогранника называют его сеткой. Построение проекций многогранника сводится к построению проекций его сетки.

Среди множества многогранников выделяют правильные многогранники. У таких многогранников все рёбра, грани и углы равны между собой. На рисунке 52, например, показан правильный многогранник, называемый октаэдром.

Среди криволинейных линейчатых поверхностей наибольшее распространение получили следующие типы поверхностей: конические, цилиндрические, с ребром возврата (торсы), с плоскостью параллелизма (поверхности Каталана), винтовые поверхности.

Рисунок 52 – Правильный многогранник

Рисунок 53 – Коническая и цилиндрическая поверхности

Коническая поверхность образуется прямой линией l (образующей), перемещающейся вдоль кривой линии m (направляющей) и имеющей неподвижную точку S (вершину) в соответствии с рисунком 53, а. Определитель поверхности (l,m,S).

Цилиндрическая поверхность образуется прямой линией l (образующей), перемещающейся вдоль кривой линии m (направляющей) и имеющей постоянное направление s в соответствии с рисунком 53, б. Определитель поверхности (l,m,s).

Поскольку все прямые, имеющие одно и то же направление, т.е. параллельные между собой, пересекаются в бесконечно удалённой (несобственной) точке, то цилиндрическую поверхность можно рассматривать как частный случай конической поверхности.

При задании конической и цилиндрической поверхностей на комплексном чертеже в качестве направляющей часто выбирают линию m пересечения поверхности с одной из плоскостей проекций.

Точки на поверхности (например, точку А на рисунке 53) строят при помощи проходящих через них образующих.

Поверхности вращения

Поверхностью вращения называется поверхность, которая описывается какой-либо образующей при её вращении вокруг неподвижной оси.

Образующая может быть как плоской, так и пространственной кривой. В частном случае это может быть прямая линия. Для задания поверхности вращения необходимо задать её ось i и какую-либо образующую l, лежащую на этой поверхности. Определитель поверхности вращения: Г(i, l). На чертеже она может быть задана проекциями этих элементов в соответствии с рисунком 54. Каждая точка L кривой l описывает при вращении окружность m с центром на оси i. Эти окружности называются параллелями поверхности. Кривые q, получающиеся в сечении поверхности вращения плоскостями (₁), проходящими через ось i, называются меридианами.

Поверхность симметрична относительно любой меридиональной плоскости, а все меридианы равны между собой. В соответствии с рисунком 54 образующая l лежит на одном из меридианов.

Если поверхность вращения расположить так, чтобы её ось i была перпендикулярна к плоскости проекций П₁, то все параллели спроецируются на эту плоскость без искажения. Меридиан q, расположенный во фронтальной плоскости (₁), называется главным меридианом. Он проецируется без искажения на плоскость проекций П₂ и определяет очертание поверхности на этой плоскости. Для построения очертания поверхности надо вращать точки образующей кривой l до их совпадения с плоскостью главного меридиана . В соответствии с рисунком 54 получена точка L, принадлежащая главному меридиану и, соответственно, очертанию поверхности. Именно таким образом строится очертание поверхности вращения по её определителю: в плоскость главного меридиана выводится определённое количество точек, соединяемых затем плавной кривой линией.

Рисунок 54 – Поверхность вращения

Параллели наибольшего и наименьшего радиусов называются соответственно экватором и горлом поверхности вращения. Они проецируются на плоскость П₁ в виде окружностей очертания. В соответствии с рисунком 54 это окружности m и m’.

Для построения точек, принадлежащих поверхности, можно использовать линии каркаса поверхности. Каркас поверхности вращения удобнее всего составлять из меридианов или параллелей, или из тех и других. Например, для нахождения второй проекции точки М(М₂), взятой на поверхности в соответствии с рисунком 54 следует провести через М₂ параллель m(m₂) и найти её горизонтальную проекцию m₁, на которой и будет находиться горизонтальная проекция М₁ точки М.

При вращении кривой второго порядка вокруг её оси образуется поверхность вращения второго порядка.

Рассматриваются следующие типы поверхностей второго порядка:

а)сфера, которая образуется вращением окружности вокруг собственной оси в соответствии с рисунком 55;

б)параболоид вращения, образуемый вращением параболы вокруг собственной оси в соответствии с рисунком 56;

в)эллипсоид вращения, который образуется вращением эллипса вокруг собственной оси. Принимая за ось вращения малую либо большую ось эллипса, получаем соответственно сжатый или вытянутый эллипсоиды вращения в соответствии с рисунками 57, а и 57, б.;

г)однополостный гиперболоид вращения, который образуется вращением гиперболы вокруг её мнимой оси в соответствии с рисунком 58, а;

д)двухполостный гиперболоид вращения, образуемый вращением гиперболы вокруг её действительной оси в соответствии с рисунком 58, б;

е)конус вращения, образуемый вращением прямой линии вокруг неподвижной оси, при этом образующая во всех своих положениях пересекает ось в некоторой точке, называемой вершиной конуса;

ж)цилиндр вращения, образуемый вращением прямой линии вокруг неподвижной оси и расположенной параллельно этой оси.

Рисунок 55 – Сфера Рисунок 56 – Параболоид вращения

Положение точки на поверхности вращения второго порядка определяют при помощи параллели или (в случае конуса и цилиндра) прямолинейной образующей, проходящих через эту точку, в соответствии с рисунками 55,56,57,58,59.

В технических деталях часто встречается поверхность вращения, называемая тором. Эта поверхность получается при вращении окружности вокруг оси, расположенной в плоскости этой окружности, но не проходящей через её центр в соответствии с рисунком 60.

В зависимости от соотношения величин радиуса образующей окружности r и расстояния от центра окружности до оси R, возможны три разновидности поверхности:

1)rR – окружность не пересекает ось – открытый тор (кольцо) в соответствии с рисунком 60;

2)r=R – окружность касается оси – закрытый тор в соответствии с рисунком 61, а;

3)rR – окружность пересекает ось – закрытый тор в соответствии с рисунком 61, б.

Произвольная прямая пересекает тор в четырёх точках и, следовательно, это поверхность четвёртого порядка.

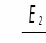
Рисунок 57 – Эллипсоид вращения

Рисунок 58 – Однополостный и двуполостный гиперболоиды

вращения

Рисунок 59 – Конус вращения и цилиндр вращения

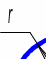
Рисунок 60 – Открытый тор

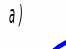
Рисунок 61 – Закрытый тор

Винтовые поверхности

Винтовой поверхностью называется поверхность, которая описывается какой-либо линией (образующей) при её винтовом движении. Если образующей винтовой поверхности является прямая, то поверхность называется линейчатой винтовой поверхностью или геликоидом.

Геликоид называется прямым (рисунок 62) или наклонным в зависимости от того, перпендикулярна образующая к оси геликоида или наклонна.

Поверхности называется закрытой или открытой в зависимости от того, пересекает образующая винтовую ось или не пересекает.

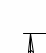
Рисунок 62- Прямой геликоид

Циклические поверхности

Циклической поверхностью называется поверхность, которая описывается какой-либо окружностью (образующей) постоянного или переменного радиуса при её произвольном движении.

Для задания циклической поверхности необходимо задать закон движения образующей и закон изменения её радиуса. К циклическим поверхностям можно отнести поверхности вращения, а также те поверхности второго порядка, которые имеют круговые сечения. Одним из частных видов циклических поверхностей являются трубчатые поверхности переменного и постоянного радиусов.

Лекция 3.1

Перпендикулярность прямых и плоскостей

Задачи, в которых определяются геометрические величины – длины отрезков, углы и т.д. – называются метрическими. Решение многих метрических задач требует построения перпендикулярных прямых и плоскостей.

Признаки перпендикулярности прямой и плоскости на комплексном чертеже устанавливаются следующей теоремой:

Для того, чтобы прямая n была перпендикулярна к плоскости Θ, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой перпендикулярна к фронтальной проекции фронтали данной плоскости (рисунок 63).

Рисунок 63 – Построение прямой, перпендикулярной к плоскости

ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА

Решение многих пространственных задач (позиционных и метрических) на комплексном чертеже часто усложняется из-за того, что заданные геометрические объекты расположены произвольно относительно плоскостей проекций и, следовательно, проецируются на эти плоскости в искажённом виде. Поэтому для более простого решения задач используют такое преобразование комплексного чертежа, которое переводило бы интересующие нас объекты из общего положения относительно плоскостей проекций в частное.

Задание на чертеже прямых и плоскостей частного положения значительно упрощает решение задач и делает его выполнимым при помощи простых замеров или простейших графических построений. Чертёж можно преобразовать, изменяя относительное расположение пространственных объектов и плоскостей проекций с целью перехода объектов от общего положения к частному. Этого можно достигнуть двумя способами:

1)заменой данной системы плоскостей проекций новой системой так, чтобы неподвижный в пространстве объект оказался в каком-либо частном положении относительно новой системы. Это способ замены плоскостей проекций;

2)перемещением объекта в пространстве так, чтобы он оказался в частном положении относительно неизменной системы плоскостей проекций. Это способ плоско параллельного перемещения и его разновидность: способ вращения вокруг проецирующей прямой.

Замена плоскостей проекций

Отличительная особенность способа замены плоскостей проекций состоит в переходе от данной системы плоскостей, в которой заданы проекции объекта, к новой системе двух взаимно перпендикулярных плоскостей. Положение самого объекта в пространстве остаётся неизменным.

Замена плоскостей проекций осуществляется последовательно.

Рассмотрим замену одной плоскости проекций. Пусть дана одна пара плоскостей проекций П₁ и П₂ (рисунок 64).

Рисунок 64 – Замена фронтальной плоскости проекций

Спроецируем какую-либо точку А на эти плоскости и определим её проекции А₁ и А₂. Возьмём новую плоскость проекций П₄, перпендикулярную к плоскости П₁, и спроецируем точку А на эту плоскость, обозначив полученную проекцию А₄. Как видно из рисунка 3.1, пара А₁ и А₄ при заданном положении плоскостей проекций П₁ и П₄ определяет в пространстве точку А.

Таким образом, мы имеем проекции точки А в старой системе (П₁, П₄) и её проекции в новой системе (П₁, П₄).

Очевидно, что обе системы абсолютно равноправны (обе фронтальные плоскости П₂ и П₄ перпендикулярны к П₁). Поэтому свойства, установленные ранее для системы (П₁, П₂) можно полностью перенести на систему (П₁, П₄). Чтобы от чертежа, выполненного в старой системе, перейти к чертежу, выполненному в новой системе, надо установить, какие из свойств остаются инвариантными (неизменными) при таком переходе от старой системы к новой. Очевидно, это будут те свойства проекций, которые связаны лишь с неподвижной плоскостью П₁, т.е. остаются неизменными:

1)горизонтальная проекция А₁ точки А;

2)высота точки А: А₁А=А₁₂А₂=А₁₄А₄₌h^А.

Аналогично можно заменить горизонтальную плоскость проекций П₁ новой плоскостью П₅, которая перпендикулярна остающейся плоскости проекций П₂ в соответствии с рисунком 65. При этом мы имеем проекции точки В(В₁, В₂) в старой системе (П₁, П₂) и её проекции в новой системе В(В₂, В₅) в новой системе (П₂, П₅). В этом случае остаются неизменными следующие свойства проекций:

1)фронтальная проекция В₂ точки В;

2)глубина точки В: В₂В=В₁₂В₁= В₂₅В₅=v^B.

На рисунке 66 показана операция перехода от системы (П₁, П₂) к системе (П₁, П₄) на комплексном чертеже.

Проведём новую ось х₁₄ и построим точку А₁₄, опуская перпендикуляр из точки А₁ на ось х₁₄. На этом перпендикуляре откладываем отрезок А₁₄А₄=А₁₂А₂=h^А. Полученная таким образом точка А₄ является проекцией точки А на плоскость П₄. О₁₂₄ – точка, у которой все три проекции совпадают.

Операция перехода от системы (П₁, П₂) к системе (П₂, П₅) на комплексном чертеже показана на рисунке 67. Линия связи В₂В₅ перпендикулярна к новой оси х₂₅.

Рисунок 65 – Замена горизонтальной плоскости проекций

Р исунок 66 – Замена фронтальной плоскости проекций

на комплексном чертеже

Рисунок 67 – Замена горизонтальной плоскости проекций

на комплексном чертеже

Рассмотрим замену двух плоскостей проекций в соответствии с рисунком 68.

Построения, выполняемые при последовательной замене двух плоскостей проекций, принципиально ничем не отличаются от тех, которые делались при однократной замене. При этом надо руководствоваться общим правилом: расстояния новых проекций точек от новой оси равны расстояниям заменяемых проекций от предыдущей оси.

Рисунок 68 – Замена двух плоскостей проекций на комплексном чертеже

Основные задачи, решаемые способом замены плоскостей проекций

Применение способа замены плоскостей проекций для решения различных задач (позиционных и метрических) основывается на четырёх основных задач.

1. Сделать прямую l(l₁,l₂) общего положения прямой уровня в новой системе плоскостей проекций.

Зададим на чертеже прямую l общего положения отрезком АВ(А₁В₁, А₂В₂) в соответствии с рисунком 69.

Рисунок 69 – Решение первой и второй основных задач

способом замены плоскостей проекций

Используя возможность свободного выбора положения оси проекций, т.е. базы отсчёта, проведём эту ось через точку А_2. Тогда высота точки А равна нулю. Чтобы прямая l стала линией уровня относительно новой плоскости проекций, плоскость П₄ должна быть параллельна l. Перейдём от системы (П₁, П₂) к системе (П₁, П₄). Новую ось х₁₄ надо провести параллельно l₁. Для построения новой проекции прямой l проведём новые линии связи, перпендикулярные оси х₁₄, и отметим на них проекции точек А и В: А₄ на оси х₁₄, поскольку h^А=0, и В₄ на высоте h^В=В₁₄В₄=В₁₂В₂. Соединив найденные точки, получим новую проекцию прямой l: l₄(А₄В₄).

Таким образом, прямая l(l₁,l₄) в новой системе плоскостей проекций (П₁, П₄) является линией уровня, поэтому отрезок А₄В₄ равен натуральному отрезку АВ, а угол , образованный проекцией А₄В₄ с осью х₁₄ равен натуральной величине угла наклона прямой l(АВ) к горизонтальной плоскости проекций П₁.

2. Сделать прямую l общего положения в новой системе плоскостей проекций проецирующей прямой в соответствии с рисунком 69.

Для преобразования прямой l в проецирующую прямую надо сначала решить первую задачу, рассмотренную выше, затем заменить ещё одну плоскость проекций, перейдя от системы (П₁, П₄) к системе (П₄, П₅).

Новую плоскость проекций П₅ выбираем перпендикулярно к плоскости проекций П₄ и одновременно перпендикулярно к прямой АВ (это возможно, поскольку АВDП₄), добиваясь этим, что прямая АВ становится проецирующей

линией (АВП₅).

На чертеже новую ось проекций надо провести перпендикулярно к А₄В₄ (х₄₅А₄В₄). Следовательно, линии связи А₄А₅ и В₄В₅ будут в данном случае совпадать с прямой А₄В₄. Откладывая на линии связи от новой оси х₄₅ отрезок v^l, равный глубине точек прямой l относительно плоскости П₄, получим проекцию заданной прямой на плоскость П₅ в виде точки l₅А₅В₅.

3. Сделать плоскость  общего положения проецирующей плоскостью в новой системе плоскостей проекций в соответствии с рисунком 70.

Зададим на чертеже плоскость общего положения  треугольником АВС(А₁В₁С₁, А₂В₂С₂). Чтобы сделать плоскость  проецирующей, надо заменить плоскость П₂ новой плоскостью П₄, выбрав её перпендикулярной к .

Для этого проведём в плоскости  горизонталь h(h₁, h₂) и новую плоскость проекций П₄ выберем перпендикулярной к этой горизонтали, а, значит, перпендикулярной и к незаменяемой плоскости проекций П₁. Тогда горизонталь h, а вместе с ней и данная плоскость , станут проецирующими относительно плоскости П₄.

На комплексном чертеже проводим новую ось х₁₄ перпендикулярно к горизонтальной проекции горизонтали: х₁₄h₁. Для удобства старую ось выбираем проходящей через самую низкую точку С₂ (при этом х₁₂С₁С₂). Строим на соответствующих новых линиях связи новые проекции точек А₄, В₄, С₄, которые располагаются на одной прямой – новой проекции плоскости (₄).

Рисунок 70 – Решение третьей и четвёртой основных задач

способом замены плоскостей проекций

Итак, плоскость (АВС) стала проецирующей. Угол , образованный проекцией плоскости А₄В₄С₄ с осью х₁₄ равен натуральной величине угла наклона плоскости  к горизонтальной плоскости проекций П₁.

4. Сделать плоскость  общего положения плоскостью уровня в новой системе плоскостей проекций в соответствии с рисунком 70.

Для преобразования плоскости  в плоскость уровня надо сначала решить третью задачу, рассмотренную выше. Затем надо перейти от системы плоскостей проекций (П₁, П₄) к новой системе (П₄, П₅), т.е. заменить плоскость П₁ новой плоскостью П₅, параллельной плоскости .

Для этого на чертеже нужно провести новую ось х₄₅, параллельную ₄ или совпадающую с ней. Выберем второй вариант. На линиях связи А₄А₅ и С₄С₅ (эти линии перпендикулярны х₄₅) откладываем отрезки А₄А₅=А₁₄А₁ и С₄С₅=С₁₄С₁; точка В₅ совпадает с В₄. Соединив точки, получаем новую проекцию А₅В₅С₅ плоскости АВС.

Итак, плоскость АВС(А₄В₄С₄, А₅В₅С₅) стала плоскостью уровня относительно плоскости П₅, а проекция А₅В₅С₅ равна натуральной величине треугольника АВС.

Плоскопараллельное перемещение

Преобразование чертежа можно осуществить и таким путем: оставив плоскости проекций неподвижными, переместить объект в пространстве как твердую систему до желаемого положения. Такое перемещение в пространстве, при котором все точки объекта перемещаются в плоскостях, параллельных между собой, называется плоскопараллельным.

Правила, позволяющие по проекциям данного положения перемещающегося объекта найти проекции конечного (искомого) положения, устанавливаются следующей теоремой:

Если объект совершает плоскопараллельное движение относительно горизонтальной плоскости проекций, то фронтальные проекции его точек будут двигаться по прямым, перпендикулярным к линиям связи; при этом горизонтальная проекция перемещающегося объекта движется по плоскости проекций, оставаясь равной самой себе.

Рисунок 71- Плоскопараллельное движение отрезка относительно горизонтальной плоскости проекций

Теорема справедлива и для плоскопараллельного движения объекта относительно фронтальной плоскости проекций.

Лекция 4.1

Под позиционными задачами понимают задачи на определение общих элементов различных геометрических объектов. К ним относят задачи на взаимную принадлежность и задачи на пересечение различных геометрических объектов.

Пересечение поверхности с линией (рисунок 72).

Рисунок 72 – Пересечение поверхности с линией

Решение основывается на следующем способе:

1)через линию l проводят вспомогательную поверхность Θ;

2)находят линию b пересечения вспомогательной поверхности Θ с данной поверхностью Ω.

3)отмечают точку А пересечения полученной линии b с данной линией l;

4)определяют видимость l линии относительно поверхности Ω.

Для простоты решения выбирают такую вспомогательную поверхность, чтобы линию пересечения её с данной поверхностью можно было строить как можно проще. Такой поверхностью является цилиндрическая проецирующая поверхность.

Частным случаем данной задачи является пересечение плоскости с прямой линией. Здесь в качестве вспомогательной поверхности используется проецирующая плоскость.

Пересечение поверхности с плоскостью

Это есть позиционная задача на определение для данных геометрических объектов их общего элемента, которым является кривая линия.

Для её построения используются вспомогательные плоскости-посредники частного положения, одновременно пересекающие данные поверхность и плоскость.

Построение линии b пересечения фронтально проецирующей плоскости  с поверхностью закрытого тора выполнено в соответствии с рисунком 73. Для этого введён ряд вспомогательных горизонтальных плоскостей –посредников Г(Г₂), Г(Г₂), Г(Г₂) и т.д. Плоскость Г(Г₂) пересекает поверхность закрытого тора по окружностям l(l₁,l₂), а плоскость  она пересекает по фронтально проецирующей прямой (3-3 ). Проекции этой прямой на чертеже обозначены следующим образом: горизонтальная – (3₁-3₁) и фронтальная - (3₂3₂). Точки 3 и 3 в силу проецирующего положения плоскости  являются одновременно и точками линии b как линии пересечения плоскости  с данной поверхностью закрытого тора. Все другие точки линии b определяются аналогично точкам 3 и 3 при помощи плоскостей-посредников Г, Г и т.д. Проекции линии b на чертеже обозначены следующим образом: фронтальная – b₂₂ и горизонтальная – b₁, представляющая собой плавную кривую, соединяющую точки 3, 3 и т.д. Следует заметить, что при построении линии b в первую очередь надо отметить точки 1 и 2 как опорные. Положение этих точек при данном расположении на чертеже поверхности закрытого тора и плоскости  определяется наличием общей плоскости симметрии (₁), которая является плоскостью главного меридиана поверхности закрытого тора. Действительно, плоскостью симметрии плоскости (₂) будет вообще любая плоскость, к ней перпендикулярная, а плоскостью симметрии поверхности будет всякая плоскость, проходящая через её ось. Общая плоскость симметрии должна удовлетворять обоим указанным условиям и очевидно, что такой плоскостью будет (₁). В силу этого линия b тоже симметрична относительно плоскости , а её горизонтальная проекция симметрична относительно следа плоскости ₁. Точки 1 и 2 лежат на главном меридиане поверхности. Отметив их фронтальные проекции 1₂ и 2₂, найдём горизонтальные проекции этих точек (1₁ и 2₁) на горизонтальной проекции главного меридиана.

Рисунок 73 – Пересечение плоскости с поверхностью закрытого тора

Рисунок 74 – Пересечение гранной поверхности с плоскостью

Построение линии пересечения гранной поверхности с плоскостью выполнено в соответствии с рисунком 74.

Сечение многогранника может быть ограничено только отрезками прямых. Число сторон такого многогранника равно числу граней многогранника, пересекаемых плоскостью. Вершинами многоугольника сечения являются точки пересечения рёбер многогранника с секущей плоскостью. Следовательно, число вершин многоугольника равно числу рёбер многогранника, пересекаемых плоскостью.

Следует заметить, что вершинами многоугольника сечения являются точки пересечения секущей плоскости с рёбрами многогранника в собственном смысле. Это значит, что точки пересечения секущей плоскости с продолжением рёбер не могут являться вершинами многоугольника сечения как не принадлежащие поверхности многогранника, но могут быть использованы для удобства построения.

Аналогично, сторонами многоугольника сечения могут являться только те отрезки прямых, которые принадлежат граням в собственном смысле.

В данном примере пирамида пересекается с фронтально проецирующей плоскостью (₁). Решение получается простым, поскольку фронтальная проекция сечения вырождается в отрезок прямой линии, совпадающей с фронтальным следом плоскости . Горизонтальной проекцией сечения является пятиугольник с вершинами 1₁, 2₁, 4₁, 5₁, 3₁.

Сечение поверхности плоскостью положено в основу ГОСТ 2.305-68 (раздел- разрезы, сечения).

Конические сечения

Линии, которые получаются при пересечении поверхности конуса второго порядка с плоскостью, называются коническими сечениями.

К этим линиям относятся следующие: эллипс, парабола, гипербола, окружность, две прямые.

Рассмотрим, при каких условиях получается то или иное сечение на примере пересечения конуса второго порядка проецирующей плоскостью (рисунок 75).

Рисунок 75 – Конические сечения

Если секущая плоскость ¹(¹₂) пересекает все образующие конуса, то в сечении получается эллипс.

Если секущая плоскость (₂) перпендикулярна к оси вращения конуса, то в сечении получается окружность.

Если секущая плоскость ²(²₂) параллельна одной образующей конуса, то в сечении будет парабола.

Если секущая плоскость ³(³₂) параллельна двум образующим конуса, то получим гиперболу.

Гипербола может быть получена и в случае расположения секущей плоскости ⁴(⁴₂) параллельно оси конуса. В этом случае плоскость параллельна двум образующим, проекции которых совпадают с проекцией оси.

Две прямые в сечении получаются, если секущая плоскость ⁵(⁵₂) проходит через вершину конуса.

Пример построения сечения конуса по параболе показан на рисунке 76. При построении сначала определялись опорные (экстремальные) точки 1, 2, и 2. Затем определялись промежуточные точки с помощью горизонтальных плоскостей-посредников Г(Г₂). Их построение можно видеть на примере точек 3 и 3.

Рисунок 76 – Сечение конуса по параболе