
Введение.
Начальные понятия общей алгебры.
(Лекция 1.)
С простейшими алгебраическими операциями – арифметическими действиями над числами – мы встречаемся еще в начальной школе, но об алгебре говорим только тогда, когда приступаем к решению задач, содержащих буквенные переменные – известные и неизвестные. Тождественные преобразования буквенных выражений, решение алгебраических уравнений, где под буквами понимаются действительные или комплексные числа, составляют содержание элементарной алгебры. Одна из основных проблем здесь – решение уравнения n-ой степени в радикалах
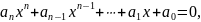
Т.е.
задача отыскания формул, выражающих
корни уравнения через его коэффициенты
при помощи простых арифметических
операций – сложения, вычитания, умножения
и деления – и процедур извлечения
корней. Например, для уравнения второй
степени
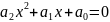 эти формулы имеют вид
эти формулы имеют вид
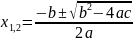
Похожие формулы есть и для уравнений третьей (формула Кардано) и четвертой (формула Феррари) степени. Однако для уравнений, степень которых выше четвертой, подобные формулы, вообще говоря, получить нельзя. Этот результат, опубликованный Нильсом Хенриком Абелем в 1824 году, не приостановил попыток исследования уравнений высших степеней. К этому времени уже было известно, что всякое уравнение n-ой степени с комплексными коэффициентами имеет ровно n комплексных корней, и усилия математиков были направлены на описание классов уравнений, для которых решение все-таки может быть получено в радикалах, и на установление условий, обеспечивающих подобную разрешимость. Эта задача была блестяще решена молодым французским математиком Эваристом Галуа, чьи результаты стали известны широкой математической общественности в 1830 году (полное изложение результатов Галуа было дано Жозефом Лиувиллем в 1846 году).
Работа Галуа стала основой новой алгебраической идеологии – он перенес центр тяжести исследования (в данном случае задачи решения уравнений) с собственно задачи на методы ее решения. Введенные им при этом понятия группы, поля, композиционного ряда и др. надолго определили путь развития алгебры. В частности, понятие группы оказалось столь плодотворным в разных областях математики (в геометрии – группы преобразований, в теории чисел – группы вычетов, в линейной алгебре – группы матриц, в топологии – гомологические группы) и естествознания (группы симметрий в кристаллографии и квантовой механике), что стало одним из центральных объектов приложения сил математиков различных направлений.
Дальнейший прогресс в алгебре связан с распространением понятия алгебраической операции с чисел на объекты нечисловой природы – элементы абстрактных групп, матрицы, кватернионы, подстановки и т.п. все это привело к постепенному переносу интересов алгебраистов с исследования конкретных объектов (уравнений, систем уравнений и т.д.) на абстрактные – группы, кольца, поля, модули – и на изучение произвольных алгебраических операций.
Именно абстрактные алгебраические операции и абстрактные алгебраические системы являются предметом изучения современной алгебры, которая окончательно сформировалась в первой половине XX столетия под влиянием работ Д.Гильберта, Э.Артина, О.Ю.Шмидта, Б.Л.Ван-дер Вардена, А.И.Мальцева, Дж. Биркгофа и др.
Теория множеств.
Множество. Равные множества. Пустое и универсальное множества.
Некоторые символьные обозначения, используемые для краткого изложения материала:
] - пусть,
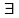 - существует,
- существует,
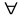 - для любых, произвольный,
- для любых, произвольный,
! – единственный,
{ - множество всех,
}- и только их,
: (|) – выполняется (такие что),
- тогда и только тогда.
Множеством будем называть совокупность объектов произвольной природы мыслимых как единое целое.
Определение. Произвольный объект по отношению к множеству называется элементом.
Определение.
Если элемент
 является объектом множества
является объектом множества
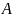 ,
то говорят, что элемент
принадлежит множеству
.
Обозначается
,
то говорят, что элемент
принадлежит множеству
.
Обозначается
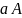 .
.
Определение. Если элемент не является объектом множества , то говорят, что элемент не принадлежит множеству . Обозначается .
Чтобы определить некоторое множество , необходимо объяснить, как отвечать на следующий вопрос: принадлежит данный объект множеству или нет?
Определение.
Множества, состоящие из одних и тех же
элементов, называются равными.
Обозначение:
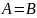 .
.
Определение. Пустым называется множество, не содержащее ни одного элемента.
Обозначение:
 .
.
Определение.
Множество
,
называется подмножеством множества
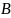 ,
если все элементы множества
принадлежат множеству
,
если все элементы множества
принадлежат множеству
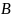 .
Обозначение:
.
Обозначение:
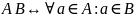 .
.
Определение. Множество называется собственным подмножеством множества , если множество является подмножеством множества и множества и неравны.
Обозначение:
 .
.
Отношение подмножества обладает рядом очевидных свойств:
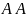 для любого множества
,
для любого множества
,Из
 и
и
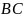 следует, что
следует, что
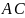 .
.
Свойство 1 - называется свойством рефлексивности подмножества, а свойство 2 - транзитивности.
Определение. Множество называется универсальным, если любое другое множество, по отношению к нему является его собственным подмножеством.
Обозначение:
 .
.
Существуют различные способы задания множеств, перечислим некоторые из них:
1.
Перечислением всех его элементов:
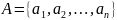 .
.
2. С
помощью характеристического свойства:
 ,
где
,
где
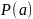 – характеристическое свойство, которым
обладают все элементы множества
,
и только они.
– характеристическое свойство, которым
обладают все элементы множества
,
и только они.
3. Графический
Над множествами можно выполнять некоторые операции, то есть некоторому множеству или множествам ставить в соответствие некоторое новое множество.
Объединение.
Объединением двух множеств называется новое множество, которое состоит из всех элементов принадлежащих множеству или множеству .
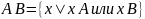
Пересечение.
Пересечением двух множеств называется новое множество, которое состоит из всех элементов принадлежащих множествам и одновременно.

Разность.
Разностью двух множеств и , называется новое множество состоящие из всех элементов множества и не принадлежащих множеству .

Дополнение.
Дополнением
множества
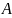 ,
называется новое множество состоящие
из всех элементов универсального
множества не принадлежащих множеству
.
,
называется новое множество состоящие
из всех элементов универсального
множества не принадлежащих множеству
.

Определение. Множества и называются неравными, если существует хотя бы один элемент одного множества не принадлежащий другому множеству.
Следствие. (Метод встречных включений.) Множества и равны, тогда и только тогда, когда множество является подмножеством множества и множество является подмножеством множества .
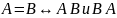 .
.
Доказательство. Необходимость. Пусть , тогда по определению равных множеств они состоит из одних и тех же элементов. Следовательно, все элементы множества являются элементами множества , и значит является подмножеством . Нетрудно показать и обратное – является подмножеством множества .
Достаточность.
Пусть
и
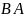 .
Предположим ,что
.
Предположим ,что
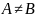 ,
тогда существует хотя бы один элемент
множества
не принадлежащий множеству
(или наоборот). В этом случае получим
противоречие с тем, что
.
Следовательно, предположение неверно,
и значит
.
,
тогда существует хотя бы один элемент
множества
не принадлежащий множеству
(или наоборот). В этом случае получим
противоречие с тем, что
.
Следовательно, предположение неверно,
и значит
.
Пример.
Проверить равенство множеств методом
встречных включений:

Решение.
Обозначим через
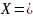
 ,
,
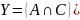 .
Тогда:
.
Тогда:
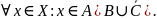 Следовательно,
Следовательно,
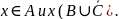 Из
Из
 следует, что
следует, что
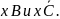 Следовательно,
Следовательно, Таким образом, получили, что
Таким образом, получили, что
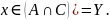 В силу выбора элемента
В силу выбора элемента
 ,
это означает, что
,
это означает, что
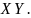
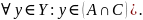 Следовательно,
Следовательно,
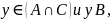 то есть
то есть
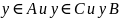 ,
и значит
,
и значит
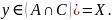 В силу выбора элемента
В силу выбора элемента
 ,
это означает, что
,
это означает, что
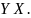
Из
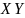 и
и
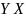 ,
на основании метода встречных включений,
следует, что
,
на основании метода встречных включений,
следует, что
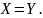
Свойства операций над множествами.
Мощность множества.
(Лекция 2.)
Коммутативность.
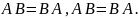
Ассоциативность.
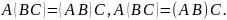

Идемпотентность.
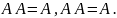
Свойства поглощения.
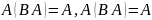
Свойства де Моргана.
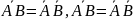
Свойства пустого и универсального множеств.
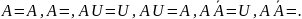
Свойство двойного дополнения.

Свойство исключения разности.
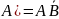 .
.
Дистрибутивность.
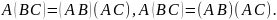
Пример:
Проверить равенство множеств:
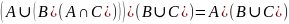 .
.
Решение:
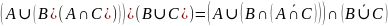 =
=
=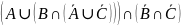 =
=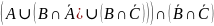 =
=
= =
=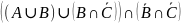 =
=
=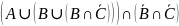 =
= =
=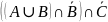 =
=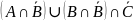 =
=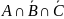 =
=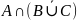 =
=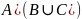 .
.
Определение. Мощностью множества называется количество всех его элементов.
Обозначение:
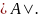
Определение.
Совокупность множеств
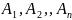 – называется разбиением множества
,
если
– называется разбиением множества
,
если
 и
и
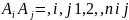 .
.
Теорема. (Метод включения и исключения) Мощность объединения множеств и равна разности суммы мощностей каждого из множеств и мощности их пересечения.
 .
.
Доказательство. Пусть
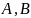 - произвольные множества тогда
- произвольные множества тогда
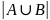 - все элементы множеств
или
,
а элементы принадлежащие одновременно
множествам
и
принадлежат их пересечению. Посчитаем
сумму
- все элементы множеств
или
,
а элементы принадлежащие одновременно
множествам
и
принадлежат их пересечению. Посчитаем
сумму
 .
При подсчёте в эту сумму войдут все
элементы множества
и множества
,
но элементы пересечения содержатся в
каждом множестве, а значит количество
элементов суммы
больше количества элементов множества
на
количество элементов пересечения.
Следовательно,
.
.
При подсчёте в эту сумму войдут все
элементы множества
и множества
,
но элементы пересечения содержатся в
каждом множестве, а значит количество
элементов суммы
больше количества элементов множества
на
количество элементов пересечения.
Следовательно,
.
Утверждение теоремы можно обобщить и для произвольного количества множеств.
Предлагается самостоятельно доказать справедливость равенства:
 .
.
А
так же сформулировать общее правило
вычисления мощности объединения
 множеств.
множеств.
Бинарные отношения.
(Лекция 3.)
Понятие отношения в математике служит для теоретико-множественного описания связей между элементами множеств.
Определение. Прямым произведением n множеств называется множество
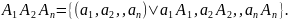
Определение. Элементы прямого произведения n множеств называются упорядоченными n-ками или кортежами длины .
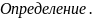 Прямым произведением двух множеств
и
называется множество
Прямым произведением двух множеств
и
называется множество
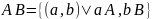 .
.
Определение. Упорядоченными парами называются элементы прямого произведения двух множеств.
Упорядоченные пары обладают следующим свойством:
Свойство.
Если
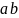 ,
то
,
то
 .
.
Определение. n-арным отношением называется всякое подмножество прямого произведения множеств.
Определение. Бинарным отношением называется всякое подмножество прямого произведения двух множеств.
Определение. Бинарным отношением называется множество некоторых упорядоченных пар.
Бинарные
отношения будем обозначать символами
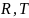 .
.
Будем
говорить, что задано бинарное отношение
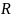 на множестве
,
если
на множестве
,
если
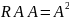 .
.
Свойства бинарных отношений заданных на множестве :
Рефлексивность. Бинарное отношение , заданное на множестве рефлексивно тогда и только тогда, когда
 .
.Антирефлексивность. Бинарное отношение , заданное на множестве антирефлексивно тогда и только тогда, когда .
Симметричность. Бинарное отношение , заданное на множестве симметрично тогда и только тогда, когда из того, что
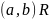 ,
всегда следует, что
,
всегда следует, что
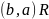 .
.Антисимметричность. Бинарное отношение , заданное на множестве антисимметрично тогда и только тогда, когда из того, что и всегда следует, что
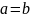 .
.Транзитивность. Бинарное отношение , заданное на множестве транзитивно тогда и только тогда, когда из и
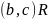 всегда следует, что
всегда следует, что
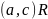 .
.Связность. Бинарное отношение , заданное на множестве связно тогда и только тогда, когда
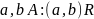 или
или
.
или
или
.
Пример. Проверить свойства бинарного
отношения
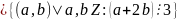 .
.
Решение.
Рефлексивность.
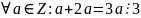 - верно.
- верно.Антирефлексивность.
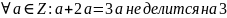 .
Для a=1, следует, что
1+21=3
.
Для a=1, следует, что
1+21=3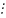 3
– неверно.
3
– неверно.Симметричность. Из
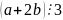 следует, что
следует, что
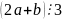 .
Так как
.
Так как
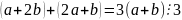 ,
то из
следует, что
– верно.
,
то из
следует, что
– верно.Антисимметричность. Из и , следует, что . Из
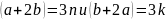 ,
следует, что
,
следует, что

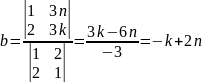 – неверно.
– неверно.Транзитивность. Из и
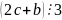 ,
следует, что
,
следует, что
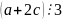 .
.
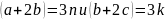 ,
следует, что
,
следует, что
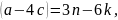
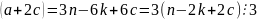 - верно.
- верно.Связность.
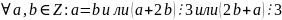 .
Для
.
Для
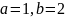 - неверно.
- неверно.
Бинарное отношение обладает свойствами рефлексивность, симметричность и транзитивность. Следовательно, - отношение эквивалентности.
