1. Понятие о функциональной полноте систем булевых функций. Операция замыкания и замкнутые классы. Теоремы о функциональной полноте систем булевых функций. Базис класса и способы его определения для заданной системы булевых функций. Примеры функционально полных систем в Р₂.

Система булевых функций полна в Р₂, если любая булева функций может быть задана в виде суперпозиции над этой системой функций. Очевидным примером функционально полной в Р₂ системы является система {&, ,}, так как в соответствии с теоремой Шеннона о разложении булевых функций по переменным любая булева функция может быть представлена формулой над этим множеством функций, а именно, СДНФ и СКНФ. Оказывается, что существуют различные функционально полные системы булевых функций. Пусть имеется некоторое множество булевых функций G={g₁,g₂,…,g_m}, и требуется определить, является ли оно функционально полным в Р₂. В теории булевых функций существует два критерия функциональной полноты системы булевых функций: сравнение заданной системы функций с заведомо функционально полной системой и критерий Поста.

Первый критерий основывается на теореме о доказательстве функциональной полноты системы булевых функций путем сравнения этой системы функций с заведомо функционально полной в Р₂ системой, которая формулируется следующим образом.

Теорема. Пусть D={f₁. f₂, …, f_n} и G={g₁, g₂, …, g_m} – подмножества множества булевых функций P₂, и известно, что система D функционально полна в Р_2. Если любая функция из D может быть получена суперпозицией функций из G, То система G также полна в Р₂.

Доказательство. Пусть F(f₁,f₂,…,f_n)P₂ – произвольная булева функция, полученная суперпозицией функций из Р₂. Так как по условию теоремы 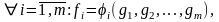где _iG, суперпозицию F(f₁,f₂,…,f_n) можно представить как F(₁(g₁,g₂,…, g_m), ₂(g₁,g₂,…, g_m), …, _n(g₁,g₂,…, g_m))= (g₁,g₂,…, g_m). Следовательно, произвольная булева функция может быть представлена суперпозицией функций из G.

Примеры:

1. Пусть D={&, , } – заведомо функционально полная система, и G={&, }. Докажем, что система G функционально полна в Р₂. Так как функции &,  уже имеются в G, остается показать, что функция  может быть определена суперпозицией над G. Воспользовавшись правилом де Моргана, получаем сразу , т.е. представляем дизъюнкцию суперпозицией над G.

2. Доказать, что система G={0, } функционально полна в Р₂.

Выберем в качестве заведомо функционально полной системы множество D={&, }. Для доказательства необходимо определить конъюнкцию и отрицание формулами над G. Целесообразная последовательность действий состоит в определении вначале , а затем &. Поскольку константа 0 – нульместная функция, ее можно использовать только для подстановки в качестве аргумента в другие функции. Импликация – двуместная функция, в которой можно выполнить вначале отождествление переменных, а затем подстановку константы вместо одного из аргументов. Учитывая, что , и выполняя подстановку xy| _{y  0} = . Далее используем правило де Моргана для получения конъюнкции.

Доказанная теорема дает универсальный способ доказательства функциональной полноты системы булевых функций. Однако если в проверяемое множество входят функции, более сложные, чем элементарные, процедура может оказаться достаточно трудоемкой. А учитывая отсутствие критерия, определяющего возможность получения требуемых функций из имеющихся, и невыполнимой.

Второй критерий, обозначенный выше как теорема Поста, лишен этих недостатков. Прежде чем перейти к нему введем несколько новых понятий.

2. Класс функций, сохраняющих нуль: признак принадлежности функции к классу, доказательство замкнутости класса, мощность класса. Привести примеры элементарных булевых функций, сохраняющих нуль.

Определение функции, сохраняющей 0:

.

Пусть функция сохраняет 0. Тогда на нулевом наборе значений переменных значение функции равно 0, а на всех остальных наборах значений переменных функция может принимать произвольные значения. Поскольку число строк таблицы равно 2ⁿ, то число строк, на которых функция может принимать произвольные значения равно 2ⁿ-1, число n-местных булевых функций, сохраняющих 0, равно числу слов длины 2ⁿ-1 в двоичном алфавите, те равно числу размещений с повторениями из 2 по 2ⁿ-1. Таким образом, число n-местных булевых функций, сохраняющих 0 равно половине от числа всех n-местных булевых функций. |T₀(n)|= .

Приведенное выше рассуждение, определяющее мощность класса Т₀ означает замкнутость класса. Докажем это явно. Пусть имеется множество 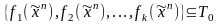. Покажем, что произвольная суперпозиция этих функций также будет сохранять 0. Пусть суперпозиция получена подстановкой функций из заданного множества вместо аргументов функции F. Очевидно, что на нулевом наборе значений переменных каждая из функций суперпозиции обращается в 0. В свою очередь Следовательно, суперпозиция функций, сохраняющих 0 также сохраняет 0. Т.е. класс функций, сохраняющих 0, замкнут. Способ построения таблицы всех n-местных булевых функций подтверждает, что

.

Элементарные булевы функции сохраняют 0. Функция отрицания , импликация, эквивалентность, штрих Шеффера, стрелка Пирса нуль не сохраняют. Из существования функций, не сохраняющих 0 следует, что класс Т₀ не полон в Р₂.

Пример. Получим константу 1 и функцию отрицания из импликации.

.

.

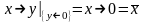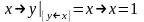Лемма о функции, не сохраняющей 0: Если , то из нее, подстановкой, сохраняющих 0 функций 0 и х, можно получить константу 1 или функцию отрицания .

3. Предполные классы. Теорема о замкнутости предполных классов.

Замыканием множества D называется процедура получения всех возможных функций суперпозицией функций из D и отождествлением переменных, обозначается [D]. Например, [{&,,}]=P₂, так как согласно доказанной ранее теореме произвольная булева функция может быть представлена булевой формулой. Замыкание одноэлементного множества {x} определим единственной возможной подстановкой:

Таким образом, замыкание рассматриваемого множества содержит ровно две функции: тождественную функцию х и саму функцию отрицания : .

Замыкание двухэлементного множества {0,1} не содержит никаких новых функций кроме констант 0 и 1, поскольку это нульместные функции и никакие подстановки не возможны. Поэтому [{0,1}]={0,1};

Замыкание двухэлементного множества может быть получено подстановками:

и .

Тогда .

Пусть М Р₂. Операция получения множества [M] из М называется операцией замыкания. Множество М называется функционально замкнутым классом, если [M]=M. Множество всех булевых функций является функционально замкнутым классом.

Пусть М – замкнутый класс в Р₂. DM называется функционально полной системой в М, если [D] = M. Множество D называется неприводимой системой, если замыкание любого его собственного подмножества отлично от замыкания D. Например, множество является функционально полной и неприводимой системой в классе , а не является.

Функции f1 и f₂ называются конгруэнтными, если одна из них может быть получена из другой заменой переменных (без отождествления). Например, функции и - конгруэнтные, а функции x&y и z&z – нет.

Множество Q булевых функций называется предполным классом в Р₂, если замыкание его есть истинное подмножество Р₂, но при добавлении к этому множеству произвольной, не принадлежащей ему функции f, получается функционально полная в Р₂ система функций:

, и .

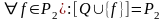Покажем, что предполный класс замкнут. Доказываем от противного. Пусть и пусть имеется функция 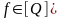. Тогда . Но , следовательно, т.е. , что противоречит определению предполного класса. Следовательно, такой функции не существует, т.е. предполный класс замкнут.

В теории булевых функций рассматриваются пять предполных классов.

4. Класс функций, сохраняющих единицу: признак принадлежности к классу, доказательство замкнутости класса, мощность класса. Привести примеры элементарных булевых функций, сохраняющих единицу.

.

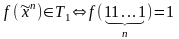Доказательство замкнутости класса функций, сохраняющих 1, и определение мощности этого класса аналогично приведенным выше доказательствам для класса функций Т₀.

Мощность класса Т₁ равна .

, а .

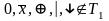Пример. Получим константу 0 и функцию отрицания из функции .

.

.

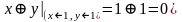Лемма о функции, не сохраняющей 1: Если , из нее подстановкой сохраняющих 1 функций 1 и х можно получить константу 0 или функцию отрицания .

5. Класс линейных функций: признак принадлежности функции к классу линейных функций, доказательство замкнутости класса линейных функций, мощность класса линейных функций, привести примеры элементарных линейных булевых функций. Способы построения полиномов по mod 2.

n-местная булева функция называется линейной, если степень задающего ее полинома по mod2 (полинома Жегалкина) не превышает 1. Чтобы определить отношение булевой функции к классу линейных функций достаточно построить ее полином. Функция линейна, если ее полином не содержит монотонных конъюнкций ранга выше 1.

.

Класс линейных функций замкнут, так как любые суперпозиции линейных функций порождают только линейные функции. Полином n-местной функции содержит коэффициентов. Каждому набору коэффициентов соответствует единственная линейная функция. Число таких функций равно числу двоичных слов длины n+1. Следовательно, мощность класса линейных функций . . Существование нелинейных функций доказывает неполноту класса L.

6. Класс самодвойственных функций: признак принадлежности функции к классу самодвойственных, доказательство замкнутости класса, мощность класса. Лемма о несамодвойственной функции. Привести примеры самодвойственной функции и применения леммы о несамодвойственной функции.

Двойственная формула, задающая некоторую булеву функцию, определяется как отрицание внешней выполняемой функции в формуле от отрицаний переменных. Соответственно класс самодвойственных функций – это множество функций, равных своим двойственным. Самодвойственная функция принимает на противоположных наборах противоположные значения.

.

Очевидно, что каждому набору значений переменных функции соответствует единственный противоположный набор. Поэтому число пар противоположных наборов равно . При принятом правиле построения таблицы булевой функции достаточно записать все наборы значений переменных в верхней половине таблицы. Далее все самодвойственные функции можно записать следующим образом. Записать всех возможных функций в верхней половине таблицы. А значения функций в нижней половине таблицы получить зеркальным инвертированием верхней половины. Нетрудно показать, что нет двуместных самодвойственных функций, существенно зависящих от обеих переменных. Из элементарных булевых функций самодвойственными являются тождественная функция и функция отрицания.

Докажем, что класс самодвойственных функций замкнут. Имеется множество самодвойственных функций . Для доказательства замкнутости класса достаточно показать, что произвольная суперпозиция самодвойственных функций также является самодвойственной. Образуем суперпозицию . Запишем двойственную к ней формулу и выполним преобразования для доказательства замкнутости класса.

Мощность класса n-местных самодвойственных функций равна .

Неполнота класса S в Р₂ доказывается существованием несамодвойственных функций.

Лемма о несамодвойственной функции: если , то из нее подстановкой самодвойственных функций х и можно получить константы 0 и 1.

Пусть . Т.е имеется, по крайней мере, одна пара противоположных наборов значений переменных, на которых функция принимает одно и то же значение:

Произведем подстановку следующего вида: Будем при этом иметь в виду, что по определению первичного терма . Следовательно, полученная таким образом суперпозиция окажется функцией одной переменной с отрицанием или без отрицания, т.е. . Рассмотрим значения этой суперпозиции при x=0 b x=1.

.

Очевидно, что полученное выражение определяет константу.

Пример «работы» леммы над несамодвойственной функцией. Пусть функция задана вектором (1011 1001). Здесь наборы с номерами 3 и 4 являются противоположными, и . МДНФ для этой функции имеет вид

.

Выполним подстановку значений переменных на наборах 3 и 4 в формулу.

Таким образом, получена константа 1. Из наборов с номерами 1 и 6 можно получить константу 0.

7. Класс монотонных функций: признак принадлежности функции к классу, доказательство замкнутости класса, примеры элементарных булевых функций, принадлежащих к классу. Лемма о немонотонной функции. Привести примеры применения леммы о немонотонной функции.

.

Из приведенного определения следует, что функция тогда и только тогда, когда на наборах значений переменных, находящихся в отношении предшествования, значения функции находятся в отношении .

Два булевых вектора и находятся в отношении предшествования тогда и только тогда, когда одноименные координаты этих векторов находятся в отношении : . например, в случае трех переменных наборы их значений имеют номера от 0 до 7. Соответственно отношение предшествования на этих наборах определяется так:

Мажоритарная функция в соответствии с определением является монотонной, а трехместная функция XOR – нет, .

Докажем, что класс монотонных функций замкнут. Пусть . Определим суперпозицию функций из этого множества . Докажем, что полученная функция монотонна. Выберем два произвольных набора значений переменных, находящихся в отношении предшествования: и определим значения каждой из функций суперпозиции на этих наборах. В силу монотонности функций, составляющих суперпозицию, . Поэтому наборы значений функций, образующих суперпозицию на наборах значений переменных, также находятся в отношении предшествования:

.

Но i( ), следовательно . Следовательно, произвольная суперпозиция монотонных функций также монотонна. Следовательно, класс монотонных функций замкнут.

Лемма о немонотонной функции: если , из нее подстановкой монотонных функций х, 0. 1 можно получить немонотонную функцию отрицания.

Пусть . Тогда найдется хотя бы одна пара наборов значений переменных и , находящихся в отношении предшествования, на которых значения функции находятся в отношении >. Предположим, что расстояние Хемминга между этими наборами равно 1, т.е. они различаются по одной координате. Пусть это будет координата x_i. Очевидно, что x_i.=0 на наборе и x_i.=1 на наборе . Тогда, подставляя эти наборы в , получим функцию одной переменно x_i.:

, .

Так как функция не монотонна, то

.

Соотношение определяет одноместную функцию отрицания.

Если , то следует найти в множестве промежуточных наборов два таких соседних набора, на которых происходит нарушение монотонности. После этого задача сводится к предыдущему примеру.

Пример применения леммы о немонотонной функции. Рассмотрим элементарную булеву функцию , вектор значений которой имеет вид: . Это двуместная функция, нулевой набор предшествует второму, расстояние Хемминга между ними равно 1 по первой переменной и . Вторая переменная в обоих наборах равна 0, а первая принимает оба возможных значения (мелькает). «Работа» леммы над этой функцией представлена ниже:

.

В соответствии с леммой из немонотонной функции получена одноместная функция отрицания.