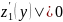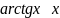билеты по матану
.docxПредел функции

 определена
в открытом интервале
определена
в открытом интервале
 ,
содержащем точку
,
содержащем точку
 ,
за исключением может быть самой точки
,
за исключением может быть самой точки
Определение
Число А называется пределом функции в точке x0 (или при x–>x0) если для любого ε>0 найдется δ>0, такое что для всех x, удовлетворяющих условию |x-x0|<δ, x≠x0 справедливо неравенство |f(x)-A|<ε
Предел на бесконечности
Число А называется пределом функции при x–>∞ если для любого положительного ε (ε>0) найдется δ>0, такое что для всех x, удовлетворяющих условию |x|>δ, справедливо неравенство |f(x)-A|<ε
Бесконечно малая функция
Функция
называется
бесконечно малой в точке a,
если

Бесконечно большая функция
Функция
называется
бесконечно большой при x–>x0,
если
 (обратная
величина к бесконечно малой)
(обратная
величина к бесконечно малой)
Если
–
б.б. при
 ,
то в окрестности точки
функция
не является ограниченной, обратное
утверждение неверно, т.е. функция может
быть неограниченна, но не быть бесконечно
большой.
,
то в окрестности точки
функция
не является ограниченной, обратное
утверждение неверно, т.е. функция может
быть неограниченна, но не быть бесконечно
большой.
Если
при
является
бесконечно большой ( )
и
)
и
 ,
то
,
то

 ,
то
,
то

Свойства бесконечно малых:
Сумма бесконечно малых бесконечно мала

– бесконечно малая
 – бесконечно
малая
– бесконечно
малая



Произведение бесконечно малой на ограниченную является бесконечно малой
Функция
называется ограниченной
в точке
 на некотором промежутке
на некотором промежутке
 ,
если для любого из этого промежутка
выполняется неравенство
,
если для любого из этого промежутка
выполняется неравенство
 ,
где
,
где
 – какое-то фиксированное число. Пример:
– какое-то фиксированное число. Пример:
 (ограничена на любом промежутке, т.к.
(ограничена на любом промежутке, т.к.
 )
)
– бесконечно малая

 – бесконечно
малая равносильны
– бесконечно
малая равносильны
( )
Произведение бесконечно малых является бесконечно малым
– бесконечно малая
– бесконечно малая
ограничена в районе точки
 – бесконечно
малая
– бесконечно
малая
Свойства пределов:
Предел суммы равен сумме пределов
Если
 ,
то
,
то

Доказательство:
 – б.м.
– б.м.
 – б.м.
– б.м.
 – сумма
бесконечно малых бесконечно малая
– сумма
бесконечно малых бесконечно малая
Предел произведения равен произведению пределов
Если
,
то

, имеющая предел в точке , ограничена в окрестности этой точки
Доказательство:


Постоянный множитель выносится за знак предела


Предел частного равен частному предела, если предел знаменателя отличен от нуля
Если
 ,
то
,
то

Доказательство:
 – ?
– ?
 – б.м?
– б.м?

 – ограничена
при
– ограничена
при
![]()
Односторонние пределы
Если
в определении предела вместо условия
|x-a|<δ,
x≠a
наложить условие a<x<a+δ,
то мы получим односторонний предел

Если
a-δ<x<a,
то мы получим предел слева

Если предел слева и справа совпадают, то существует общий предел
 =>
=>
Основные пределы анализа (Замечательные пределы)
Доказательство:

Теорема о сжатой переменной
Если
при
,
 и
и
 ,
тогда
,
тогда

случай
 .
Рассмотрим единичную окружность
.
Рассмотрим единичную окружность








При


Тогда
Если
 ,
то
,
то
Если
 ,
то
,
то
Доказательство:

Доказательство:


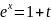



1
С ледствие:
ледствие:

 ,
,
Доказательство:





Эквивалентные БМФ
Бесконечно
малые функции
 и
и
 называются
эквивалентными, если при
,
называются
эквивалентными, если при
,


|
|
|
|
|
|
|
|
|
|
При вычислении предела произведения и частного бесконечно малые можно заменять на эквивалентные



Доказательство:

Замечание: В сумме или разности заменять бесконечно малые на эквивалентные вообще говоря нельзя
Непрерывные функции
Пусть точка x0 является внутренней точкой области определения функции y=f(x)
Функция
f(x)
называется непрерывной в точке x0,
если

Все элементарные функции непрерывны во внутренних точках области определения
Элементарные функции:
степенные:

показательные:

логарифмические:

основные тригонометрические:

обратные тригонометрические
f(x)
называется непрерывной на промежутке
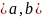 ,
если она непрерывна во всех точках
этого промежутка
,
если она непрерывна во всех точках
этого промежутка
Классификация точек разрыва
Т очки,
в которых функция является не непрерывной,
называются точками разрыва (подразумевается,
что функция определена в окрестности
точки разрыва)
очки,
в которых функция является не непрерывной,
называются точками разрыва (подразумевается,
что функция определена в окрестности
точки разрыва)
 предел
существует, но функция в точке x0
не определена
предел
существует, но функция в точке x0
не определена
В это случае точка x0 называется точкой устранимого разрыва
скачок
Точка x0 называется точкой скачка функции f(x), если в этой точке пределы слева и справа существуют, но не равны между собой

Устранимые разрывы и скачки называются разрывами первого рода
x0 называется точкой бесконечного разрыва функции, если

x0 называется точкой существенного(неустранимого) разрыва функции f(x), если
 не
существует ни в конечном, ни в бесконечном
виде
не
существует ни в конечном, ни в бесконечном
виде
Бесконечные и неустранимые разрывы называются разрывами второго рода
Производная*
Производной
функцией
 в
точке
в
точке
 называется
называется
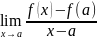
Функция должна быть определена в самой точке a и в ее окрестности
Геометрический смысл производной
В
 пределе секущая становится касательной
к графику функции. Касательная – это
предельное положение соответствующей
секущей. При малых
пределе секущая становится касательной
к графику функции. Касательная – это
предельное положение соответствующей
секущей. При малых
 секущая идет практически по графику
функции.
секущая идет практически по графику
функции.
Геометрический смысл производной состоит в том, что она совпадает с tg угла наклона касательной к графику функции в точке x0
Производная отвечает за возрастание и убывание функции. Там, где производная положительна, функция возрастает (причем, тем быстрее, чем производная). Там, где производная отрицательна, функция убывает
Табличные производные*
|
|
|
|
|
|
|
|
|
|
|
|
Свойства производных*
Дифференцирование – линейная операция

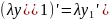
Производная произведения
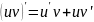
Производная частного

Производная сложной функции
 сложная
функция
сложная
функция

Доказательство:

Производная обратной функции
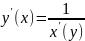
Дифференциал

 -
дифференциал
функции y
-
дифференциал
функции y

Дифференциалом функции в точке называется



Дифференциал является функцией двух аргументов:
и
Свойства дифференциалов:
Дифференциал является главной частью приращения функции
( )
)

 – б.м.
– б.м.


![]()

при
малых
:

Если
 ,
то
,
то





Теорема Лагранжа (Формула конечных приращений)
П усть
функция
усть
функция
 непрерывна
и дифференцируема на промежутке
непрерывна
и дифференцируема на промежутке
 ,
тогда внутри промежутка найдется точка
c,
такая что:
,
тогда внутри промежутка найдется точка
c,
такая что:



Теорема
Лагранжа утверждает,
что на кривой
найдется
такая точка с,
в которой касательная параллельна
хорде AB
утверждает,
что на кривой
найдется
такая точка с,
в которой касательная параллельна
хорде AB

 – формула
конечных приращений
– формула
конечных приращений



Монотонные функции*
Убывающие или возрастающие функции называются монотонными
Функция
 называется монотонно возрастающей на
промежутке
называется монотонно возрастающей на
промежутке
 ,
если для любых
,
если для любых и
и
 выполняется
неравенство
выполняется
неравенство

 строго
возрастающая
строго
возрастающая
 нестрого
возрастающая
нестрого
возрастающая
Функция
называется монотонно убывающей на этом
промежутке, если
 (строго
убывающая)
(строго
убывающая)
Теорема Лагранжа (достаточное условие монотонности функции)
Если для всех точек промежутка
 ,
то функция
возрастает
,
то функция
возрастает
 ,
то функция
убывает
,
то функция
убывает
Доказательство:
Зафиксируем любые точки и на интервале, такие что
Согласно
теореме Лагранжа:
 ,
где
,
где

По
условию на всем интервале
.
Следовательно,

 ,
т.к.
,
т.к.
Тогда
 =>
=>
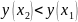 => функция
убывает
=> функция
убывает
Промежутки монотонности дифференцируемой функции
На
промежутках, где производная сохраняет
знак, функция является монотонной.
Таким образом, промежуток монотонного
возрастания может смениться промежутком
монотонного убывания только в тех
точках, где производная меняет знак ( или не существует)
или не существует)
Для того чтобы найти промежутки возрастания и убывания дифференцируемой функции необходимо:
взять ее производную
найти точки, в которых производная равна нулю или терпит разрыв
посмотреть на знаки производной между этими точками
Экстремум*
Точка называется точкой экстремума функции, если:
она является внутренней точкой ООФ
промежуток возрастания в этой точке сменяется промежутком убывания или наоборот
Необходимое условие для наличия экстремума
Необходимым условием для наличия экстремума функции одного аргумента является обращение в нуль (или разрыв) производной этой функции
Если промежуток возрастания сменяется промежутком убывания, то точка экстремума называется максимумом (локальным)
Если промежуток убывания сменяется промежутком возрастания, то точка экстремума называется минимумом(локальным)
Замечание:
Максимум и минимум не нужно путать с наибольшим и наименьшим значением функции на промежутке
Острый экстремум – точка разрыва производной. К такому экстремуму нельзя построить касательную
Правило Лопиталя
Правило
Лопиталя годится для раскрытия
неопределенности типа
 ,
косвенно и для других видов
,
косвенно и для других видов
Если
 ,
то
,
то

Замечание:
Правило Лопиталя можно применять в случае, если

Правило Лопиталя применяется и в случае неопределенности типа


 и
и

Правило Лопиталя применяется ко всем другим типам неопределенности
Частная производная*
Рассмотрим
функцию
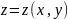 .
Зафиксируем
переменную y:
.
Зафиксируем
переменную y:

Тогда мы получим функцию от одной переменной x. Производная этой функции по переменной x называется частной производной z по x

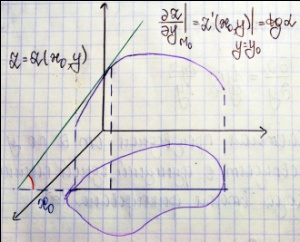 ;
;

Геометрический смысл частных производных
Частная
производная отвечает за возрастание
и убывание функции
 в направлении переменной
в направлении переменной
 (т.е. когда
(т.е. когда
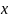 фиксирована). Точно также
фиксирована). Точно также
 отвечает за возрастание и убывание
функции
в направлении переменной
(т.е. когда
фиксирована).
отвечает за возрастание и убывание
функции
в направлении переменной
(т.е. когда
фиксирована).
Экстремум функции двух переменных
Т очка
очка
 называется точкой максимума функции
называется точкой максимума функции
 ,
если:
,
если:
Точка является внутренней точкой ООФ
Существует круг на плоскости
 с центром в точке
,
такой, что для всех точек
из этого круга выполняется неравенство
с центром в точке
,
такой, что для всех точек
из этого круга выполняется неравенство

Понятие максимума есть понятие локальное также как и для функции одного аргумента

 может
не быть наибольшим значением функции
во всей области. Является локальным
наибольшим
может
не быть наибольшим значением функции
во всей области. Является локальным
наибольшим
Точка называется точкой минимума функции, если:
Точка не лежит на границе ООФ
Существует круг с центром в точке , такой что для всех точек из этого круга выполняется неравенство

Точки максимума и минимума вместе называются точками экстремума
Необходимое условие для наличия экстремума
Пусть
функция
 имеет
экстремум в точке
имеет
экстремум в точке

Зафиксируем
переменную
и рассмотрим функцию
 .
Эта
функция имеет экстремум в точке
.
Эта
функция имеет экстремум в точке

Необходимым условием для наличия экстремума функции одного аргумента является обращение в нуль (или разрыв) производной этой функции
Предположим,
что функция дифференцируема, тогда