билеты 1-40

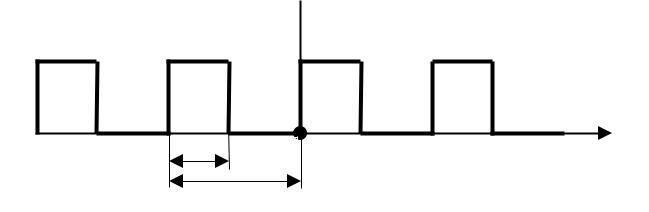
Билет 1 Детерминированные сигналы

Детерминированные сигналы подразделяяются на периодические и непериодические. К периодическим относятся сигналы, значение которых повторяется через некоторый фиксированный интервал времени. Минимальный интервал времени, через который сигнал повторяет свое значение, называется периодом периодического сигнала.

Для непериодического сигнала не существует интервала времени, через который сигнал повторяет свое значение.

Периодический сигнал описывается функцией, для которой выполняется условие:

s(t) =s(t +n ×T ),

(1.1.1)

где

n – любое целое число, как положительное, так и отрицательное; T – период сигнала.

Пример периодического сигнала приведен на рис.1.1.

s(t)

	E
	t
τи	0
	T
Рис. 1.1. Последовательность прямоугольных импульсов длительностью τ и периодом Т.

Простейшим периодическим сигналом является гармонический сигнал, который описывается функцией вида:

s(t) = А ×Соs(ωt +ϕ),

(1.1.2)

где А – амплитуда гармонического сигнала, ω - частота гармонического сигнала (измеряется в рад/сек), φ – начальная фаза гармонического сигнала, ω = 2 π f,

f – циклическая частота (измеряется в Гц или в 1/сек).

Важнейшим свойством гармонического сигнала является то, что при прохождении через линейные электронные цепи этот сигнал не меняет своей формы, а изменяет только амплитуду и начальную фазу. Это свойство позволяет использовать гармонические колебания при анализе линейных цепей.

Из математики известно, что

	е jα = Cosα + jSinβ .							(1.1.3)
	Тогда
	s(t) =Re Aе j (ωt +ϕ)							(1.1.4)
	или	jϕ		jωt		jωt	,	(1.1.5)
	s(t) =Re Aе		×е
					=Re A ×е

где A = Aе jϕ – комплексная амплитуда гармонического колебания.

Комплексной амплитудой гармонического колебания называется такое комплексное число, модуль которого равен действительной амплитуде гармонического колебания, а аргумент – начальной фазе гармонического колебания.

Билет 2. Спектры периодических сигналов.

Рассмотрим произвольный периодический сигнал с периодом Т (рис.1.2). s(t)

t

T

Рис. 1.2. Произвольный периодический сигнал с периодом Т.

Из математики известно, что на интервале Т сигнал можно представить в виде набора гармонических колебаний вида (разложение в ряд Фурье):

s(t) = a0 + å[anCos(nΩt) +bn Sin(nΩt)],

(1.2.1)

∞

2

n=1

где ao/2, an, bn – коэффициенты ряда Фурье, которые связаны с сигналом s(t)

следующими выражениями:

a0

1

T 2

2

T 2

2

T 2

=

ò

s(t)dt,

an =

ò

s(t)Cos(nΩt)dt,

bn =

ò

s(t)Sin(nΩt)dt,

2

T

T

T

−T 2

−T 2

−T 2

(1.2.2)

где Ω = 2π/T – основная частота периодического сигнала или частота первой гармоники сигнала, частоты ωn = nΩ называются частотами высших гармоник сигнала.

Выражение (1.2.1) можно переписать в виде:

			a0		∞
s(t) =				+ åAnCos(nΩt +ϕn ),			(1.2.3)
		2		n=1				ϕn = arctg bn
где An = (an		2 ) + (bn			2 ) - действительная амплитуда		n-ой гармоники сигнала,
								an

- начальная фаза n – ой гармоники сигнала.

Выражение (1.2.3) называется рядом Фурье в тригонометрической форме.

Величина ао /2 называется постоянной составляющей сигнала или его средним значением.

Совокупность амплитуд (An) гармонических составляющих сигнала и ао/2 называется амплитудным спектром периодического сигнала или его амплитудно-частотной характеристикой (АЧХ).

Совокупность начальных фаз (φn) гармонических составляющих сигнала называется фазовым спектром периодического сигнала или его фазочастотной характеристикой (ФЧХ).

Совокупность амплитуд (An), (φn), ао /2 и Ω полностью определяют периодический сигнал.

Выражение (1.2.3) можно представить в комплексном виде

					1	∞		jnΩt
		s(t) =			2 nå=−∞Ane				,	(1.2.4)
		2 T 2
		T	ò			−jnΩt
где	An =			s(t)e			dt.

−T 2

Учитывая, что An - четная, а φn - нечетная функции частоты, и используя формулы Эйлера уравнение 1.2.4 легко переходит в уравнение 1.2.3.

1.2.1. Распределение мощности в спектре периодических сигналов

Под средней за период мощностью периодического сигнала понимается величина

				1	Tòs2 (t)dt.
	P =	s2 (t)	=			(1.2.6)
				T 0

мощность периодического сигнала, выделяемого на единичном сопротивлении в виде

	∞
P = s2 (t) = 0,25A02	+ 0,5åAn2 ,	(1.2.1)

n=1

где P= = s2 (t) = 0,25A02 - мощность постоянной составляющей периодического сигнала;

∞

P≈ = 0,5åAn2 , - мощность переменной составляющей периодического сигнала.

n=1

Введем понятие ширины спектра периодического сигнала.

Под шириной спектра периодического сигнала понимается интервал частот ∆ω, внутри которого сосредоточено 90% переменной мощности сигнала.

Ширина спектра периодического сигнала находится из выражения

N
P≈ = 0,5åAn2 = 0,9P≈ , откуда ∆ω = NΩ.	(1.2.11)
n=1
Это определение справедливо для периодических	сигналов, максимальные

составляющие амплитудного спектра которого лежат вблизи начала координат.

Для периодических сигналов, максимальные составляющие амплитудного спектра которого лежат вблизи некоторой частоты ωо, ширина спектра находится из условия

n0 + N

P≈ = 0,5 åAn2−n0 = 0,9P≈ , , где no находится из выражения ωо = noΩ,

n=n0 −N

а N соответствует крайним составляющим спектра периодического сигнала ωн = ωо – N Ω и ωв = ωо+N Ω, где ωо – частота составляющей спектра сигнала с максимальной амплитудой.

Тогда ширина спектра определится как	∆ω = 2NΩ.
1.2.2. Некоторые свойства спектров периодических сигналов
1. Если сигнал четный, т.е. s(t) = s(-t), то	bn = 0,	An =		an		,

		ì0,	an > 0,					(1.2.12)
	ϕn = í		an < 0.
		îπ ,
2. Если сигнал нечетный, т. е. s(t) = - s(-t), то a0 / 2 = 0, аn = 0, An =					bn		,
	ìπ 2,	bn	> 0,					(1.2.13)
	ϕn = í	bn	< 0.
	îπ 2,
3.	Интервал между соседними линиями спектра периодического сигнала равен

частоте основной гармоники сигнала и с увеличением периода уменьшается.

Билет 3. Спектры непериодических сигналов.

Рассмотрим произвольный периодический сигнал, изображенный на рис. 1.5.

s(t)

t

T

Рис. 1.5. Произвольный периодический сигнал с периодом Т.

Представим этот сигнал в виде ряда Фурье в комплексной форме

∞

jnΩt

.

s(t) = 0,5 åAne

Учитывая, что

n=−∞

2 T 2

An =

òs(t)e

−jnΩt

dt.

T

получим

−T 2

T 2

∞

2

s(t) =0,5 å

òs(t)e−jnΩt dte jnΩt .

(1.3.1)

n=−∞ T

T 2

−

Так как Т = 2π/Ω, то последнее выражение перепишется в виде

∞

T 2

s(t) =(1/ 2π) å

òs(t)e− jnΩt dte jnΩt Ω.

(1.3.2)

n=−∞

T 2

−

Для получения непериодического сигнала из заданного периодического устремим

период сигнала s(t) к бесконечности.

При Т→ ∞

непериодический сигнал s1(t), совпадающий на интервале периода с s(t),

будет определяться как

s (t) = lim s(t) = lim(1/ 2π)

∞

T 2

å

ò

s(t)e− jnΩt dte jnΩt Ω

.

(1.3.3)

1

T

→∞

T

→∞

n=−∞

T 2

−

При T→∞ частота Ω стремится к dω, nΩ – к текущей частоте ω, а операция

суммирования переходит в операцию интегрирования.

С учетом выше изложенного, получим

∞ ∞

s(t) = (1/ 2π) ò òs(t)e− jωt dt ×e jωt dω.

(1.3.4)

−∞−∞

Из последнего выражения получим

∞

S( jω) = òs(t)e− jωt dt – прямое преобразование Фурье и

−∞

∞

s(t) = (1/ 2π) òS( jω) ×e jωt dω. – обратное преобразование Фурье.

−∞

S(jω) называется спектральной плотностью непериодического сигнала. S(jω) также, как и s(t) полностью описывает сигнал. S(jω) и s(t) описывают сигнал в разных системах координат.

Так как S(jω) представляет комплексную функцию частоты, то S(jω) можно представить в алгебраической

	экспоненциальной		S ( jω) = A(ω) + jB(ω) и							(1.3.5)
			S ( jω) = S (ω)eϕ(ω) ,							(1.3.6)
	где
							ϕ(ω) = arctg B(ω) .
	ω =
		2	ω +	2	ω
	S ( j )	A	( )	B	( ) ,
								A(ω)

S(ω) называется спектральной плотностью амплитуд, а φ(ω) – спектральной плотностью фаз непериодического сигнала.

Билет 4. Спектр прямоугольного импульса.

Пример. Дано: прямоугольный сигнал, изображенный на рис.1.6. Найти: S(jω), S(ω) и φ(ω), построить графики.

s(t)

Е

t

Приведенный

сигнал

в

-τ/2

0 τ/2

Рис.1.6.

аналитическом виде

-τ / 2 £ t £ τ / 2,

ì E,

=

s(t) = í

-τ ³ t

и t ³ τ

/ 2.

î0,

τ / 2

τ / 2

− jωt

E ×e−iωt

S( jω) = òE ×e

dt =

;

- jω

−τ / 2

−τ / 2

S ( jω) =

E(eiωτ / 2 −eiωτ / 2 )

или

− jω

S( jω) = Eτ

Sin(ωτ / 2)

,

откуда

ωτ / 2

ì

0,

S( jω) > 0,

ωτ

S( jω) = Eτ

Sin(

/ 2)

,

ϕ(ω) = í

ωτ / 2

îπ ,

S( jω) < 0.

Графики S(ω) и φ(ω) приведены на рис.1.7.

S(ω)
	φ(ω)
ω	2π/τ	4π/τ	6π/τ	ω

0

2π/τ

4π/τ 6π/τ

a)

-π

б)

1.7. Спектральные плотности амплитуд (а) и фаз (б) прямоугольного импульса.

Билет 5. Свойства преобразования Фурье.

1. Свойство линейности

Если s(t) = a × s1 (t) +b ×s2 (t) +c ×s3 (t) ), где а, в, с – вещественные числа.

Тогда

S( jω) = a × S1 ( jω) +b × S2 ( jω) + c × S3 ( jω) , где	(1.3.7)
где S1(jω), S2(jω), S3(jω) – спектральные плотности сигналов	s1(t), s2(t), s3(t)
соответственно, а S(jω) спектральная плотность сигнала s(t).
1. Свойство четности.
s(t) – четная функция, т. е. s(t) = s(-t)

S(jω )=	¥ò	s(t)e- jω tdt=	¥ò	s(t)Соsω t×dt-	j¥ò	s(t)Sinω t×dt	(1.3.8)
	-	¥	-	¥	-	¥

Второй интеграл равен нулю, так как подинтегральная функция нечетная.

Таким образом S( jω ) = ∞òs(t)Соsωt ×dt , а так как подинтегральная функция четная, то

			−∞
S( jω ) = A(ω ) = 2∞ò s(t)Соsωt ×dt					.	(1.3.9)
0
S(ω) =		A(ω)	ì0,	A(ω) > 0,
			, ϕ(ω) = í
			îπ ,	A(ω) < 0.

3.Свойство нечетности.

s(t) – нечетная функция, т. е. s(t) = - s(-t)

S(jω )=	¥ò	s(t)e- jω tdt=	¥ò	s(t)Соsω t×dt-	j¥ò	s(t)Sinω t×dt
	-	¥	-	¥	-	¥

Первый интеграл равен нулю, так как подинтегральная функция нечетная. Отсюда

S( j		) = - j					∞	t ×dt
	ω						ò s(t)Sin
							ω		, а так как подинтегральная функция четная, то
						− ∞
S( jω ) = jB(ω ) = - j2∞ò s(t)Sinωt ×dt											(1.3.10)
							0
S(ω) =				B(ω)		,	ì π / 2,			B(ω) > 0,
							ϕ(ω) = í
							î- π / 2,			B(ω) < 0.

4. Свойство задержки.

Дан сигнал s(t), спектральная плотность которого S(jω). Найти спектральную плотность сигнала s1(t) = s(t - to). Сигнал s1(t) отличается от сигнала s(t) сдвигом на интервал τ вправо по оси времени, т.е. задержкой на время to.

Спектральная плотность сигнала s(t) будет иметь вид:
S( jω ) =	∞ò s(t)e− jωt ×dt .	(1.3.11)

−∞

аспектральная плотность сигнала s1(t)=s(t – to) вид:

S1( jω ) =			∞ò s(t - t0 )e− jωt ×dt .					(1.3.12)
			− ∞
В последнем выражении сделаем замену переменных t – to = τ.
Тогда t = τ + to, а dt = dτ					и интеграл (1.3.10)			примет вид:
			∞
S1( j	ω	) =	τ	− jωτ	e	− jωt0	τ .	(1.3.13)
			ò s( )e				×d

− ∞

Так как exp(-jωtо) не зависит от τ, то этот сомножитель можно вынести за пределы интеграла.

∞
Тогда получим S1 ( jω) = e− jωt0 òs(τ)e− jωτ ×dτ	(1.3.14)

−∞

Впоследнем выражении интеграл в скобках полностью совпадает с выражением (1.3.11),

т.е.

S1( jω) = S( jω)e− jωt0 .

(1.3.15)

Таким образом сдвиг во временной области на время t0 вправо по оси времени приводит

кумножению на exp(-jωtо) в частотной области.

5.Свойство дифференцирования.

Дан сигнал s(t), спектральная плотность которого S(jω). Найти спектральную плотность сигнала s1(t) = ds(t)/dt.

Пусть спектральные плотности сигналов s(t) и s1(t) будут S(jω) и S1(jω) соответственно.

				∞
Тогда	s(t) = (1/ 2π) òS( jω) ×e jωt dω.
				−∞
						∞
		s (t) = (1/ 2π) S ( jω) ×e jωt dω.
		1				ò	1
					−∞
Найдем
			d	∞
s1	(t) =			[(1/ 2π) òS( jω) ×e jωt dω].
			dt
				−∞

(1.3.16) а

(1.3.17)

(1.3.18)

Меняя порядок дифференцирования и интегрирования и, продифференцировав по t, получим

∞
s1 (t) = (1/ 2π) òS( jω) × jω ×e jωt dω.	(1.3.19)
−∞
Сравнивая (1.3.17) и (1.3.19), получаем
S1 ( jω) = S( jω) × jω,	(1.3.20)

т .е. дифференцирование во временной области приводит к умножению на jω в частотной области.

6. Свойство интегрирования.

Дан сигнал s(t), спектральная плотность которого S(jω). Найти спектральную плотность сигнала s1(t) = ∫s(t)dt.

Пусть спектральные плотности сигналов s(t) и s1(t) будут S(jω) и S(jω) соответственно.

Тогда

	∞				∞
π	ω	jωt	ω	π	ω	jωt ω (1.3.21)
s(t) = (1/ 2	) òS( j ) ×e	d	, s1	(t) = (1/ 2	) òS1 ( j ) ×e	d .
	−∞				−∞

	∞
Найдем	s1 (t) = ò(1/ 2π) òS( jω)e jωt dω × dt.	(1.3.22)
	−∞
Изменяя порядок интегрирования и, интегрируя по t, получим
	∞
	s1 (t) = (1/ 2π) ò[S( jω) / jω]×e jωt dω.	(1.3.23)
	−∞
Сравнивая (1.3.23) и (1.3.21), получаем
	S1 ( jω) = S( jω) / jω,	(1.3.24)

т .е. интегрирование во временной области приводит к делению на jω в частотной области.

7. Спектральная плотность сигнала при изменении масштаба времени

Пусть для сигнала	s(t), спектральная плотность которого S(jω), изменяется масштаб
времени. Введем	новое время τ = kt, где k – некоторое вещественное число.
Тогда спектральная плотность S1(jω) сигнала s(kt) будет иметь вид:

		S1( jω ) =			∞ò s(kt)e− jωt				×dt		(1.3.25)
					− ∞
или					∞
S1( j	ω	) =	1	∞	τ	− jωτ / k	×d	τ	.	и окончательно
			k	s( )e
				−ò∞
					-∞
		S1( jω) =			1 S( jω/ k).						(1.3.26)
					k

8. Спектральная плотность свертки двух сигналов

Пусть даны два сигнала s1(t) и s2(t), спектральные плотности которых равны S1(jω) и S2(jω) соответственно. Тогда свертка этих сигналов будет иметь вид

s(t) = ∞ò s1(τ )s2 (t - τ ) ×dτ .

− ∞

(1.3.27)

Найдем спектральную плотность сигнала в виде:

S(jω )=	¥òs(t)e- jω t ×dt=			¥ò	¥òs1(τ )s2(t- τ )×dτ ×e- jω tdt.
	- ¥			- ¥	- ¥
Меняя порядок интегрирования, получим
S( jω ) =		∞ò s1(τ ) ∞ò s2 (t - τ )×e− jωtdt × dτ .
		− ∞	− ∞
С учетом свойства задержки
∞ò s2 (t - τ )×e− jωtdt = S2 ( jω )e− jωτ .
− ∞
					∞	∞
Тогда	S( jω) = S2 ( jω) òs1(τ)e− jωτ dτ, а					òs1 (τ)e− jωτ dτ
					−∞	−∞

И окончательно S( jω) = S1( jω) × S2 ( jω).

(1.3.28)

= S1 ( jω).

(1.3.29)

(1.3.30)

(1.3.31)

т.е. спектральная плотность свертки двух сигналов равна произведению спектральных плотностей этих сигналов.

*) рассмотренное преобразование Фурье можно применять к сигналам, которые описываются функциями, удовлетворяющими условию абсолютной интегрируемости, которое имеет вид

∞

ò s(t) dt < ∞.

−∞

Билет 6. Операторное представление сигналов.

Пусть дан сигнал, который описывается функцией s(t), не удовлетворяющей условию абсолютной интегрируемости.