Дисперсия может быть определена методом условных моментов. Момент распределения – это средняя mотклонений значений признака от какой-либо величины А: если А = 0, то момент называется начальным; еслиА = , то моменты – центральными; если А = С, то моменты – условными.
В зависимости от показателя степени К, в которую возведены отклонения (х – А)к, моменты называются моментами 1-го, 2-го и т.д. порядков.
Расчет дисперсии методом условных моментов состоит в следующем:
1. Выбор условного нуля С;
2. Преобразование фактических значений признака х в упрощенные х´ путем отсчета от условного нуля С и уменьшения в d раз:
3. Расчет 1-го условного момента:
4. Расчет 2-го условного момента:
5. Расчет 1-го порядка начального момента:
6. Дисперсии
Средняя арифметическая
Средняя
арифметическая применяется, когда объем
совокупности представляет собой сумму
всех индивидуальных значений варьирующего
признака. Следует отметить, что если
вид средней величины не указывается,
подразумевается средняя арифметическая.
Ее логическая формула имеет вид:
Средняя
арифметическая простая рассчитывается по
несгруппированным данным по
формуле:
или 
,
где 
–
отдельные значения признака;
j
– порядковый номер единицы наблюдения,
которая характеризуется значением 
;
N
– число единиц наблюдения (объем
совокупности).
В
случае, когда данные сгруппированы по
значениям признака (т.
е. построен дискретный вариационный
ряд распределения) средняя
арифметическая взвешеннаярассчитывается
с использовании либо частот 
,
либо частостей 
наблюдения
конкретных значений признака 
,
число которых (k) значительно меньше
числа наблюдений (N) .
,
,
где
k – количество групп вариационного
ряда,
i
– номер группы вариационного
ряда.
Поскольку 
,
а 
,
получаем формулы, используемые для
практических расчетов:
и 
В
случае, когда данные сгруппированы по
интервалам,
т.е. представлены в виде интервальных
рядов распределения, при расчете средней
арифметической в качестве значения
признака принимают середину интервала,
исходя из предположения о равномерном
распределении единиц совокупности на
данном интервале. Расчет ведется по
формулам:
и 
где 
-
середина интервала: 
,
где 
и 
–
нижняя и верхняя границы интервалов
(при условии, что верхняя граница данного
интервала совпадает с нижней границей
следующего интервала).
Средняя
арифметическая обладает рядом свойств.
1.
Сумма отклонений вариант от средней
равна нулю:
.
2.
Если все значения вариант увеличиваются
или уменьшаются на величину А, то и
средняя величина увеличивается или
уменьшается на ту же величину А:
3.
Если каждую варианту увеличить или
уменьшить в В раз, то средняя величина
также увеличится или уменьшатся в
то же количество раз:
или 
4.
Сумма произведений вариант на частоты
равна произведению средней величины
на сумму частот:
5.
Если все частоты разделить или умножить
на какое-либо число, то средняя
арифметическая не изменится:
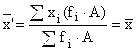6)
если во всех интервалах частоты равны
друг другу, то средняя арифметическая
взвешенная равна простой средней
арифметической:
,
где
k – количество групп вариационного
ряда.
Использование
свойств средней позволяет упростить
ее вычисление.
Допустим,
что все варианты (х) сначала уменьшены
на одно и то же число А, а затем уменьшены
в В раз. Наибольшее упрощение достигается,
когда в качестве А выбирается значение
середины интервала, обладающего
наибольшей частотой, а в качестве В –
величина интервала (для рядов с одинаковыми
интервалами). Величина А называется
началом отсчета, поэтому этот метод
вычисления средней называется способом
отсчета от условного нуля или способом
моментов.
После
такого преобразования получим новый
вариационный ряд распределения, варианты
которого равны 
.
Их средняя арифметическая, называемая моментом
первого порядка, выражаетсяформулой 
и
согласно второго и третьего свойств
средней арифметической равна средней
из первоначальных вариант, уменьшенной
сначала на А, а потом в В раз, т. е. 
.
Для
получения действительной
средней (средней
первоначального ряда)нужно момент
первого порядка 
умножить
на В и прибавить А:
