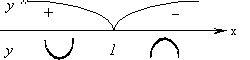Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
![]()
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :
![]()
[Править]Уравнение прямой с угловым коэффициентом
Уравнение
прямой с угловым коэффициентом.
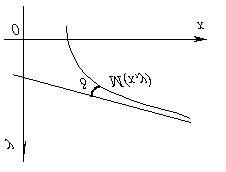
Прямая линия, пересекающая ось Oy в
точке ![]() и
образующая угол
и
образующая угол ![]() с
положительным направлением оси Ox:
с
положительным направлением оси Ox:
![]()
Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.
[Править]Уравнение прямой в отрезках
Прямая
линия, пересекающая ось Ox в
точке ![]() и
ось Oy в
точке
:
и
ось Oy в
точке
:
![]()
В этом виде невозможно представить прямую, проходящую через начало координат.
[Править]Нормальное уравнение прямой
![]()
где p —
длина перпендикуляра, опущенного на
прямую из начала координат, а θ —
угол (измеренный в положительном
направлении) между положительным
направлением оси Ox и
направлением этого перпендикуляра.
Если p =
0,
то прямая проходит через начало координат,
а угол ![]() задаёт
угол наклона прямой.
задаёт
угол наклона прямой.
БИЛЕТ 10. ЛИНИИ ВТОРОГО ПОРЯДКА.
Определение
1. Уравнение
вида (**), где хотя бы один из коэффициентов
 не равен нулю, называется уравнением
второго порядка.
не равен нулю, называется уравнением
второго порядка.
Определение 2. Линия на плоскости, координаты точек которой удовлетворяют уравнению второго порядка, называется линией второго порядка (далее обозначаем ее ЛВП).
БИЛЕТ 11. УРАВНЕНИЕ ПРЯМОЙИ ПЛОСКОСТИ В ПРОСТРАНСТВЕ.
Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (3.2)
2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:
![]() =
=![]() ;
(3.3)
;
(3.3)
3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
![]() .
(3.4)
.
(3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x1 +mt, y = y1 + nt, z = z1 + рt. (3.5)
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
![]() .
.
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
![]()
равносильна
системе ![]() ;
такая прямая перпендикулярна к оси Ох.
;
такая прямая перпендикулярна к оси Ох.
Система ![]() равносильна
системе x = x1, y
= y1;
прямая параллельна оси Oz
равносильна
системе x = x1, y
= y1;
прямая параллельна оси Oz
БИЛЕТ 14. ПРЕДЕЛ ФУНКЦИИ.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
Пусть
даны функции ![]() и
и ![]() .
.
Одна и та же функция в одной и той же точке может иметь только один предел.
![]()
Доказательство [показать]
Сходящаяся функция локально сохраняет знак. Более обще,
![]()
где ![]() —
проколотая окрестность точки a.
—
проколотая окрестность точки a.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
![]()
Сходящаяся функция локально ограничена в окрестности предельной точки:
![]()
Отделимость от нуля функций, имеющих предел, отличный от нуля.
![]()
Операция взятия предела сохраняет нестрогие неравенства.
![]()
Правило двух милиционеров
Предел суммы равен сумме пределов:
![]()
Предел разности равен разности пределов:
![]()
Предел произведения равен произведению пределов:
![]()
Предел частного равен частному пределов.

БИЛЕТ 15. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
БИЛЕТ 17. ПРИЗВОДНАЯ ФУНКЦИИ.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.
БИЛЕТ 19. ЛОГАРИФМИЧЕСКОЕ ДИФ.
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:
![]()
БИЛЕТ 20. ПРАВИЛО ЛОПИТАЛЯ.
Правило
Бернулли[1]-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида 0
/ 0 и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Условия:
 или
или 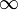 ;
;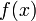 и
и 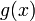 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности 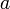 ;
; в
проколотой окрестности
;
в
проколотой окрестности
;существует
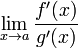 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
БИЛЕТ 22 И 23.
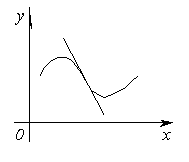
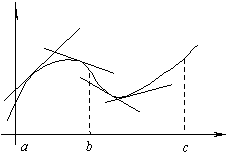
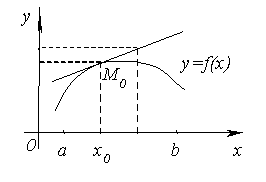
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Примеры.
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым. Возьмем
на графике функции y
= f(x) произвольную
точку M0 с
абсциссой x0 (a; b)
и проведем через точку M0 касательную.
Ее уравнение |
|
Итак,
уравнение кривой имеет вид y
= f(x).
Обозначим ![]() ординату
касательной, соответствующую абсциссе x.
Тогда
ординату
касательной, соответствующую абсциссе x.
Тогда ![]() .
Следовательно, разность ординат кривой
и касательной при одном и том же
значении x будет
.
Следовательно, разность ординат кривой
и касательной при одном и том же
значении x будет ![]() .
.
Разность f(x)
– f(x0) преобразуем
по теореме Лагранжа ![]() ,
где c между x и x0.
,
где c между x и x0.
Таким образом,
![]() .
.
К
выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: ![]() ,
где c1 между c0 и x0.
По условию теоремы f ''(x)
< 0. Определим знак произведения второго
и третьего сомножителей.
,
где c1 между c0 и x0.
По условию теоремы f ''(x)
< 0. Определим знак произведения второго
и третьего сомножителей.
Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
 (x
– x0)
> 0 и (c
– x0)
> 0. Поэтому
(x
– x0)
> 0 и (c
– x0)
> 0. Поэтому 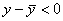 .
.Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y' = –2x, y'' = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
y = ex. Так как y'' = ex > 0 при любых x, то кривая всюду вогнута.



y = x3. Так как y'' = 6x, то y'' < 0 при x < 0 и y'' > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. Определим достаточные условия того, что данная точка кривой является точкой перегиба. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x= x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых. Найдем производные заданной функции до второго порядка.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
Возможные
точки перегиба найдем, решив уравнение
2x2 –
1 = 0. Отсюда
Точки
перегиба
Следовательно, f(x) выпуклая на (–1; 1). |
|
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
 Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем стремлении
в бесконечность должна неограниченно
приближаться к асимптоте.
Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем стремлении
в бесконечность должна неограниченно
приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
БИЛЕТ 24. ФОРМУЛА ТЕЙЛОРА.
Формула Тейлора — Пеано Пусть ![]() , z0 —
предельная точка множества Df и
, z0 —
предельная точка множества Df и ![]() .
Если функция f n-дифференцируема
в смысле
Ферма — Лагранжа в
точкеz0,
то справедлива формула Тейлора
— Пеано
.
Если функция f n-дифференцируема
в смысле
Ферма — Лагранжа в
точкеz0,
то справедлива формула Тейлора
— Пеано
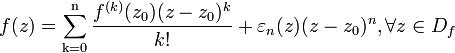
где εn(z) - непрерывная в точке z0 функция и εn(z0)=0. Применим метод математической индукции. Если n=0, то утверждение очевидно при εn (z)=f(z)-f(z0). Предположим, что утверждение теоремы справедливо после замены n на n-1 и что функция f n-дифференцируема в смысле Ферма-Лагранжа в точке z0. Согласно определению, существует такая n-1 дифференцируемая в смысле Ферма-Лагранжа в точке z0 функция φ, что ∀z∈Df,
f(z) − f(z0) = (z − z0)φ(z)(2)


 при
всех x из
(–1; 1).
при
всех x из
(–1; 1).