2. Определение области операций.

Именно такая ситуация возникает в том случае, когда h литров жидкости разлито по трем сосудом: в первом x литров, во втором – y литров и в третьем – z литров. Постепенному переливанию жидкости из второго сосуда в третий соответствует движение точки с трилинейными координатами (x, y, z) относительно треугольника АВС с высотой, равной h, по прямой x = const в направлении, соответствующем уменьшению y и увеличению z. Если каждый сосуд может вмещать h литров (такую ситуацию мы будем обозначать символом [h; h, h, h]), то каждая из координат x, y, z может принимать любое значение от 0 до h, и множество точек, в которые можно попасть, как-то переливая жидкость из одного сосуда в другой – это множество мы назовем областью операций – задается неравенствами: 0 £ x £ h, 0 £ y £ h, 0 £ z £ h, и совпадает со всем треугольником АВС.

Гораздо больший интерес представляет случай [h; a, b, c]. Здесь три данных сосуда имеют емкости a, b, c и h ³ a > b > c. Поставим задачу: нужно отмерить определенную величину d литров жидкости, многократно переливая из одного сосуда в другой; при этом разрешается только либо полностью опорожнить один сосуд, либо до краев наполнить другой (а, возможно, произойдет то и другое одновременно). Область операций теперь задается неравенствами: 0 £ x £ a, 0 £ y £ b, 0 £ z £ c, которые, как правило, определяют правильный или неправильный шестиугольник, ограниченный шестью прямыми: x = 0, y = 0, x = a, y = b, z = 0, z = c.

Но в частных случаях эта область может превратиться в пятиугольник, трапецию, параллелограмм или (как мы уже видели) охватывать весь равносторонний треугольник.

Будем считать, что числа a, b, c, h и d – целые.

3. Рассмотрение некоторых частных случаев данного метода.

На рисунках 1 и 2 проиллюстрирована ситуация [8; 7, 6, 3]: 8 литров жидкости некоторым образом разлиты в сосуды емкостью 7, 6 и 3 литров. Здесь областью операций является шестиугольник 0 £ x £ 7, 0 £ y £ 6, 0 £ z £ 3, ограниченный прямыми x = 7, z = 0, y = 6, x = 0, z = 3, y = 0. Трилинейные координаты вершин шестиугольника (относительно равностороннего треугольника с высотой 8) – (7, 1, 0), (2, 6, 0), (0, 6, 2), (0, 5 ,3), (5, 0, 3), (7, 0, 1). Допустим, что в первом сосуде находится 3 литра жидкости, во втором – тоже 3, тогда в третьем сосуде – 2 литра жидкости. Такому распределению жидкости соответствует точка с координатами (3, 3, 2). Шесть направлений, исходящих из этой точки, указывают на шесть возможных операций по переливанию. Направление от точки (3, 3, 2) к точке (5, 3, 0) соответствует процессу опустошения третьего сосуда: содержавшаяся в нем жидкость переливается в первый сосуд; противоположному же направлению – от точки (3, 3, 2) к точке (2, 3, 3) – процесс наполнения третьего сосуда: он доливается жидкостью из первого. Направлению от точки (3, 3, 2) к точке (0, 6, 2) соответствует процесс опустошения первого сосуда, содержимое которого переливается во второй сосуд; при этом второй сосуд заполняется, и т. д.

Допустим, что нам надо отмерить 4 литра жидкости (то есть получить 4 литра жидкости хотя бы в одном из сосудов). Прежде всего заметим, что при первом же разрешенном переливании жидкости мы от внутренней точки области операций переходим к ее граничной точке – таковы условия переливания. Например, красная ломаная на рисунке 2 задает один из возможных способов перехода от точки (3, 3, 2) к точке (4, 4, 0) (и, таким образом, деления восьми литров на две равные порции). Легко видеть, что звенья ломаной всегда параллельны сторонам треугольника АВС, причем ломаная «поворачивает» только тогда, когда попадает на границу области. Если теперь, не ставя перед собой задачи об отмеривании четырех литров, провести из точки (3, 3, 2) всевозможные ломаные (со звеньями, параллельными сторонам треугольника АВС, и с концами на границе нашей шестиугольной области), то рано или поздно мы побываем во всех граничных точках нашего шестиугольника. То же справедливо для любой целой точки данной области операций (как внутренней, так и граничной). Значит, каково бы ни было распределение восьми литров жидкости по сосудам для случая [8; 7, 6, 3], «доливанием» и «опорожнением» сосудов можно отмерить любое целое число литров жидкости (меньшее восьми).

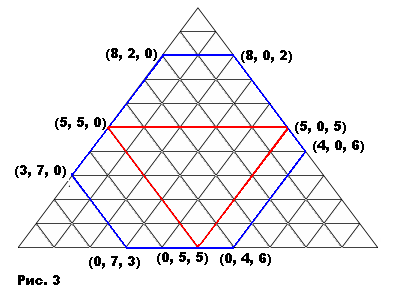
На рисунке 3 проиллюстрирован случай [10; 8, 7, 6]: 10 литров жидкости разлиты по сосудам, вмещающим 8, 7 и 6 литров. Область операций здесь снова шестиугольник. В этом случае для любого распределения десяти литров по сосудам легко отмерить d = 1, 2, 3, 4, 6, 7, 8, 9 литров жидкости. Но если с самого начала ни в одном из сосудов не содержится пяти литров жидкости, то мы эти 5 литров никогда не сможем отмерить, поскольку путь, проходящий через точки (0, 5, 5), (5, 0, 5) и (5, 5, 0), замкнут, и на него нельзя попасть ни с какого другого пути. Вообще, если h = 2d ³ a > b > c > d, то в ситуации [h; a, b, c] опустошением и доливанием сосудов d литров жидкости нельзя отмерить, как бы эти h литров ни были распределены по сосудам, если только ни в одном из сосудов первоначально не было d литров.

Рассмотрим еще случай [10; 8, 6, 4] – четное число литров жидкости разлито по сосудам с четными емкостями (рис. 4). Здесь область операций – прямоугольник. Из рисунка 4 видно, что если первоначально в каждом из сосудов было по четному числу литров, то есть исходная точка – с четными координатами (например, (6, 2, 2)), то мы никогда не сможем отмерить нечетное число литров жидкости.

Наиболее известны задачи, соответствующие случаю [h; a, b, c], где h = a = 2d = b + c. В этом случае область операции – параллелограмм с вершинами (a, 0, 0), (c, b, 0), (0, b, c), (b, 0, c),

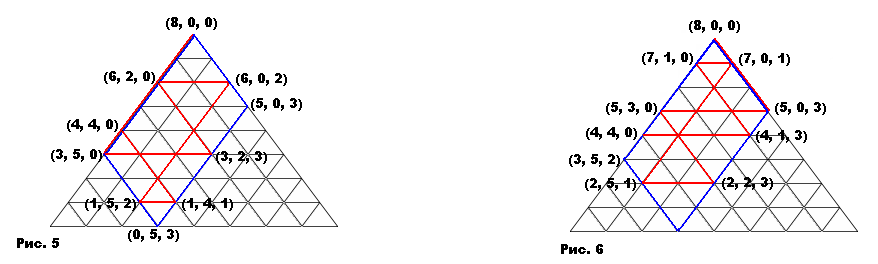
На рисунках 5 и 6 показаны два решения задачи, соответствующей случаю [8; 8, 5, 3] с исходным распределением жидкости (8, 0, 0); требуется отмерить 4 литра жидкости. Иными словами, два человека, имея сосуд, наполненный восемью литрами жидкости, и два пустых сосуда емкостью 5 литров и 3 литров, хотят разделить эти 8 литров жидкости поровну.

Первое, что нужно сделать, – это наполнить сосуд емкостью 5 литров, как на рисунке 5, либо сосуд емкостью 3 литра, как на рисунке 6. После этого всякий раз, когда ломаная попадает на одну из сторон нашего параллелограмма – прямые y = = 0, y = 5, z = 0, z = 3, – мы рассматриваем эту сторону как зеркало. (Правило зеркальных отражений объясняется тем, что каждый отрезок ломаной, параллельной стороне исходного треугольника, соответствует операции переливания жидкости из одного сосуда в другой, а третий сосуд в это время не трогают.) Таким образом, мы получаем решение (8, 0, 0) ® (3, 5, 0) ® (3, 2, 3) ® ® (6, 2, 0) ® (6, 0, 2) ® (1, 5, 2) ® (1, 4, 3) ® (4, 4, 0) и решение (8, 0, 0) ® (5, 0, 3) ® (5, 3, 0) ® (2, 3, 3) ® (2, 5, 1) ® (7, 0, 1) ® (7, 1, 0) ® (4, 1, 3) ® (4, 4, 0).

Ясно, что отмерить любое целое число литров жидкости в ситуации h = a = b + c можно лишь в том случае, когда числа a и b взаимно просты.