
5.1 Свойства формата с плавающей точкой
Избыточность. Обратите внимание на то, что в примере 5-1 одно и тоже число –3,12 можно при любом исходном положении точки записать разными способами. Это указывает на неоднозначность представления числа и избыточность формата с плавающей точкой, которые являются следствием неоднозначности представления чисел в прототипе (в полулогарифмической форме). Избыточность формата с плавающей точкой много меньше, чем прототипа.
В полулогарифмической форме одно и тоже число можно записать бесконечно большим количеством способов, изменяя его порядок или положение запятой в мантиссе. Например, число –3,12 можно записать как: –3,12100; –31,210-1; –312,010-2;…; –0, 312101; –0, 0312102; … .
В формате с плавающей точкой эти возможности весьма ограничены. При изменении порядка разряды мантиссы сдвигаются относительно положения точки, что приводит к выдвижению цифр мантиссы за пределы ее поля и к их потере. Так в примере 5-1 число –3,12 в любом из выбранных форматов можно записать только двумя способами. Попытка, например, в варианте A изменить порядок на –1 или +2 приведет к потере старшего или младшего значащего разряда из-за выдвижения их за пределы разрядной сетки мантиссы.
Избыточность формата с плавающей точкой с полями ограниченной длины проявляет себя только, если количество значащих цифр в значении числа меньше количества позиций в поле мантиссы и величина смещения запятой при размещении значащих разрядов в поле мантиссы не выходит за пределы диапазона чисел представляемых в поле порядка.
Избыточность формата является его недостатком, так как усложняет сравнение чисел. Разные коды могут иметь равные значения. Код с меньшим значением порядка может иметь большее значение, чем код с большим значением порядка. Чтобы упростить операции сравнения обычно из всех возможных вариантов записи числа в формате предпочитают только один из них, ограничивая применение других. Предпочтительным является вариант, при котором крайняя левая позиция поля мантиссы содержит код старшей значащей цифры отличной от нуля. В этом варианте во всех позициях поля мантиссы содержатся значащие цифры, что позволяет записывать число с максимальной точностью.
Мантиссу числа и число называют нормализованными, если в крайней левой позиции поля мантиссы содержится код старшей значащей цифры мантиссы, отличной от нуля. Все другие варианты записи мантиссы и числа в формате называют ненормализованными или денормализованными.
В примере 5-1 во всех строках, кроме второй, числа и их мантиссы нормализованные. Во второй строке число –3,12 денормализовано вправо.
В формат числа записывают числа нормализованные. Запись в формат ненормализованных чисел допускают лишь в некоторых особых случаях.
Особым случаем является запись чисел
![]() .
Все варианты записи этих чисел содержат
коды 0 во всех позициях поля мантиссы и
различаются лишь значением кода в поле
порядка. Поэтому записать числа
как нормализованные невозможно.
Предпочтительный способ записи кода
нуля оговаривают отдельно. Обычно
предпочитают запись нуля, содержащую
код нуля в поле мантиссы и код нуля в
поле порядка или код нуля в поле мантиссы
и код минимально возможного значения
порядка
.
.
Все варианты записи этих чисел содержат
коды 0 во всех позициях поля мантиссы и
различаются лишь значением кода в поле
порядка. Поэтому записать числа
как нормализованные невозможно.
Предпочтительный способ записи кода
нуля оговаривают отдельно. Обычно
предпочитают запись нуля, содержащую
код нуля в поле мантиссы и код нуля в
поле порядка или код нуля в поле мантиссы
и код минимально возможного значения
порядка
.
Точность формата. Существуют числа, которые нельзя разместить в формате с полями фиксированной длины. Причин этому две. Ограниченная длина поля мантиссы и ограниченная длина поля порядка.
Если количество значащих разрядов в числе превышает длину поля мантиссы, то такое число нельзя представить в формате. Например, число +2,3157601 нельзя записать в формат с полем мантиссы длиной 6 позиций при любой длине поля порядка. Выходом из этой ситуации является округление числа до требуемого числа разрядов, что приводит к погрешности в его представлении. Количество сохраняемых значащих разрядов числа является мерой точности представления числа.1
Фиксированная длина поля мантиссы ограничивает точность чисел сохраняемых в формате. В связи с этим формат характеризуют максимально возможной точностью представляемых в нем чисел и под точностью формата понимают длину поля мантиссы.
Числа, количество значащих разрядов в которых превышает точность формата, могут быть представлены с точностью формата только в нормализованной форме и для этого они должны быть округлены. Представление в нормализованной форме гарантирует, что точное число, записанное в формат после округления, имеет точность не меньше точности формата. Представление тех же чисел в ненормализованном виде приводит к снижению их точности до величины меньшей, чем точность формата на величину равную количеству нулей в поле мантиссы слева. Поэтому числа в формате с плавающей точкой следует представлять в нормализованном виде.
Числа, количество значащих разрядов в которых не превышает точность формата, могут быть представлены в формате с абсолютной точностью и погрешностью равной нулю. Нормализованная форма, и в некоторых случаях ненормализованная, обеспечивают абсолютную точность представления таких чисел. Например, ненормализованные числа во второй строке примера 5-1 имеют абсолютную точность представления.
Пример 5-2. Пусть в формате с полем
мантиссы
![]() и точкой фиксированной перед левой
позицией необходимо записать число
+3,46. Результат записи: |0|001|346000 имеет
абсолютную точность. Ненормализованные
записи этого числа |0|002|034600 и |0|004|000346
также имеют абсолютную точность.
и точкой фиксированной перед левой
позицией необходимо записать число
+3,46. Результат записи: |0|001|346000 имеет
абсолютную точность. Ненормализованные
записи этого числа |0|002|034600 и |0|004|000346
также имеют абсолютную точность.
Пусть в этом же формате необходимо
записать число +2,3157601 имеющее 8 значащих
разрядов. Это можно выполнить, округлив
число, например, отбросив «лишние»
разряды справа. В нормализованном виде
результат записи будет |0|001|231576| со
значением +0,23157610+1.
Он имеет максимально возможную точность
равную точности формата 6. В ненормализованном
виде число можно записать, сдвинув
нормализованную мантиссу на
![]() разрядов вправо и увеличив порядок на
разрядов вправо и увеличив порядок на
![]() .
Точность представления числа уменьшится
на i, т.е. на количество нулей в поле
мантиссы слева. Так при
.
Точность представления числа уменьшится
на i, т.е. на количество нулей в поле
мантиссы слева. Так при
![]() получим результат записи |0|003|002316| с
точностью 62=4. При
получим результат записи |0|003|002316| с
точностью 62=4. При
![]() результат равен |0|003|000023| с точностью 2.
При
результат равен |0|003|000023| с точностью 2.
При
![]() мантисса станет равной нулю, и точность
числа будет 0. Во всех случаях имеет
место потеря точности, но она минимальна
при нормализованном представлении
числа. Кроме того, при нормализованном
представлении точность числа гарантирована
и не меньше чем точность формата.
мантисса станет равной нулю, и точность
числа будет 0. Во всех случаях имеет
место потеря точности, но она минимальна
при нормализованном представлении
числа. Кроме того, при нормализованном
представлении точность числа гарантирована
и не меньше чем точность формата.
Ограниченный сверху диапазон
представляемых чисел. При ограниченной
длине полей порядка и мантиссы всегда
существуют максимальный порядок
и максимальная мантисса
![]() представимые в формате. Эти ограничения
приводят к следующим последствиям.
представимые в формате. Эти ограничения
приводят к следующим последствиям.
Числа после их округления, по модулю
большие, чем
![]() ,
не могут быть записаны в формат, и при
попытке их записи возникает исключительная
ситуация переполнение формата. На
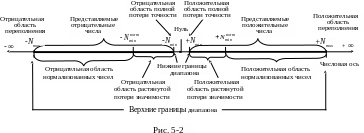
рис.5-2 показан диапазон чисел представимых
в формате с плавающей точкой и полями
фиксированной длины для случая, когда
он симметричен относительно нуля.
,
не могут быть записаны в формат, и при
попытке их записи возникает исключительная
ситуация переполнение формата. На
рис.5-2 показан диапазон чисел представимых
в формате с плавающей точкой и полями
фиксированной длины для случая, когда
он симметричен относительно нуля.
Как видно из рис.5-2 значения
![]() являются верхними границами диапазона
чисел представляемых в формате.
являются верхними границами диапазона
чисел представляемых в формате.
Существует возможность представить в
формате числа принадлежащие области
переполнения в виде нечисловых величин
![]() или
или
![]() и выполнять арифметические операции с
этими числами, например
и выполнять арифметические операции с
этими числами, например
![]()
Для этого символам
и
можно привести в соответствие коды
формата неиспользуемые для представления
чисел. Например, коды отличающиеся
знаком и кодирующие нулевую мантиссу
и порядок равный 1, или коды с
ненормализованной мантиссой и порядком
большим, чем
.
Для этого символам
и
можно привести в соответствие коды
формата неиспользуемые для представления
чисел. Например, коды отличающиеся
знаком и кодирующие нулевую мантиссу
и порядок равный 1, или коды с
ненормализованной мантиссой и порядком
большим, чем
.
Ограниченный снизу диапазон
представляемых чисел. При ограниченной
длине полей порядка и мантиссы всегда
существуют минимальный порядок
и минимальная мантисса
![]() представимые в формате. Эти ограничения
приводят к следующим последствиям.
представимые в формате. Эти ограничения
приводят к следующим последствиям.
Числа по модулю меньшие, чем
![]() ,
кроме нуля, не могут быть записаны в
формат даже в ненормализованном виде.
Аппроксимация таких чисел машинным
нулем приводит к полной потере ими
точности. Деление даже крохотного числа,
например
,
кроме нуля, не могут быть записаны в
формат даже в ненормализованном виде.
Аппроксимация таких чисел машинным
нулем приводит к полной потере ими
точности. Деление даже крохотного числа,
например
![]() ,
на машинный ноль приведет к результату
равному
,
на машинный ноль приведет к результату
равному
![]() ,
в то время как он должен был бы ненамного
превышать 1.2
,
в то время как он должен был бы ненамного
превышать 1.2
Значения
![]() являются нижними границами диапазона
чисел представимых в формате.
являются нижними границами диапазона
чисел представимых в формате.
Заметим, что существует возможность абсолютный нуль и машинный нуль представлять в формате разными кодами. Например, точный нуль записывать с порядком и мантиссой равными нулю, а машинный нуль с мантиссой равной нулю и порядком . Это позволяет при анализе операндов на нуль различать машинный и точный нуль и своевременно принимать меры для исключения ошибок в вычислениях.
Числа по модулю меньшие, чем
![]() ,
где
,
где
![]() -
минимальная нормализованная мантисса
представимая в формате, не могут быть
записаны в формат в нормализованном
виде. Значения
-
минимальная нормализованная мантисса
представимая в формате, не могут быть
записаны в формат в нормализованном
виде. Значения
![]() являются нижними границами диапазона
нормализованных чисел представимых в
формате, т.е. чисел, точность которых не
меньше точности формата.
являются нижними границами диапазона
нормализованных чисел представимых в
формате, т.е. чисел, точность которых не
меньше точности формата.
Если с целью обеспечения максимальной точности равной точности формата допускать представление чисел в формате только в нормализованном виде, то нижними границами диапазона чисел будут значения . Это приведет к расширению области полной потери точности до границ , что крайне нежелательно. Однако конструкторы некоторых ЦВМ с целью их упрощения так поступают.
Лучшим решением с точки зрения обеспечения максимально возможной точности представления чисел в формате является принятие следующего соглашения.
Все числа, которые могут быть представлены
в формате в нормализованном виде, должны
представляться нормализованными. Лишь
только в некоторых случаях в порядке
исключения можно допускать представление
этих чисел в ненормализованном виде.
Числа маленькие по абсолютной величине,
настолько маленькие, что при записи их
мантиссы в нормализованной форме
![]() порядок числа
порядок числа
![]() должны быть записаны в формат в
ненормализованном виде с порядком
.
Тогда, лишь только совсем крохотные
числа меньшие по модулю
будут принадлежать области полной
потери точности.
должны быть записаны в формат в
ненормализованном виде с порядком
.
Тогда, лишь только совсем крохотные
числа меньшие по модулю
будут принадлежать области полной
потери точности.
При таком соглашении числа с порядком и ненормализованной мантиссой принадлежат области растянутой потери значимости, поскольку их точность может снижаться по мере приближения числа к нулю и возрастает вероятность их непригодности для практического применения. Природа такой растянутости аналогична той, что имеет место в формате с фиксированной точкой (раздел 3.1). Конструкторы современных универсальных ЦВМ придерживаются этого соглашения.
Рассмотрим на примерах запись в формате рис.5-1 маленьких чисел и погрешность их представления, если допускать или запрещать запись в ненормализованном виде.
Пример 5-3. Пусть в формате с десятичной
мантиссой и порядком поле мантиссы
содержит шесть позиций, точка фиксирована
слева от старшей позиции, поле порядка
содержит позицию знака порядка и две
позиции разрядов целого. В этом формате
значение минимальной нормализованной
мантиссы
![]() ,
а минимального порядка
,
а минимального порядка
![]() .
Значение модуля минимального
нормализованного числа
.
Значение модуля минимального
нормализованного числа
![]() .
.
Пусть числа, приведенные в левой колонке табл.5.1, при записи в формат округляются до ближайшего числа.
Относительная погрешность числа записанного в формат
![]()
где N – точное значение числа;
![]() – значение числа записанного в формат.
– значение числа записанного в формат.
В варианте A представление
ненормализованного числа не допускается.
Число округлено до ближайшего, т.е. до
![]() или до нуля. Число большее, чем 0,510-100,
округляется до 0,110-99,
меньшее, чем 0,510-100,
– до нуля.
или до нуля. Число большее, чем 0,510-100,
округляется до 0,110-99,
меньшее, чем 0,510-100,
– до нуля.
В варианте B допускается представление числа в ненормализованном виде. Округление выполнено до ближайшего числа.
В варианте A только очень близкие к числа сохраняют значимость и полностью теряют ее, как только становятся меньше половины . Погрешность представления числа с его уменьшением возрастает очень быстро.
В варианте B потеря значимости растягивается на гораздо больший интервал, причем числа с малой разрядностью полностью сохраняют свою значимость до тех пор, пока сдвинутая мантисса не теряет младший значащий разряд. Погрешность представления числа с его уменьшением возрастает сравнительно медленно.
Из сказанного следует, что для достижения максимальной точности представления числа следует записывать в формат в нормализованном виде и допускать запись ненормализованных чисел только с порядком равным . При таком способе записи все числа в формате представляются однозначно.
З
Таблица 5.1
Число N
Вариант A
Вариант B
Число N0
Погрешность
Число N0
Погрешность
0,99999910-100 0,80000010-100 0,55200010-100 0,50000010-100 0,55200010-102 0,55200010-104 0,55200010-105 0,55200010-106
0,10000010-99 0,10000010-99 0,10000010-99 0 0 0 0 0
0,0001%
25%
81%
100%
100%
100%
100%
100%
0,10000010-99 0,08000010-99 0,05520010-99 0,05000010-99 0,00055210-99 0,00000610-99 0,00000110-99 0
0,0001% 0 0 0 0
8,7%
81%
100%
0,552487210-100 0,552487210-102 0,552487210-104 0,552487210-105 0,552487210-106
0,10000010-99 0 0 0 0
81%
100%
100%
100%
100%
0,05524910-99 0,00055210-99 0,00000610-99 0,000001 10-99 0
0,0005%
0,09%
8,6%
81%
100%
П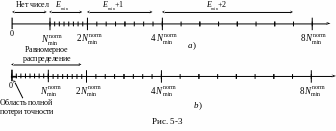 лотность
размещения чисел. Представимые
числа можно сгруппировать в интервалах
лотность
размещения чисел. Представимые
числа можно сгруппировать в интервалах
![]() ,
как показано на рис.5-3 при
,
как показано на рис.5-3 при
![]() .
Представляемые числа в положительной
области чисел отмечены на числовой оси
вертикальными черточками.
.
Представляемые числа в положительной
области чисел отмечены на числовой оси
вертикальными черточками.
Рис.5-3a иллюстрирует случай
представления в формате только
нормализованных чисел с длиной поля
мантиссы 4 бита. В пределах одного
интервала порядок числа неизменен,
изменяется только мантисса, и поэтому
соседние числа отличаются на одинаковую
величину. Следовательно, числа на
интервале распределены равномерно, и
плотность распределения чисел сохраняется
постоянной. Каждый последующий интервал
в P раз шире предшествующего, а
количество чисел в нем остается прежним.
Поэтому плотность распределения
изменяется в P раз. Интервал
![]() равен по ширине интервалу
равен по ширине интервалу
![]() .
Однако представимых чисел на
интервале
нет, и он принадлежит области полной
потери точности.
.
Однако представимых чисел на
интервале
нет, и он принадлежит области полной
потери точности.
Вообразите теперь, что длина мантиссы не 3 бита, а реальная, например 20 бит. Тогда на интервале разместится не 8, а 220 чисел. Промежуток между соседними числами можно будет увидеть разве что под микроскопом. При этом на соседнем интервале чисел по-прежнему не будет. Едва ли можно такой способ представления маленьких чисел признать удовлетворительным.
Рис.5-3b иллюстрирует, что произойдет,
если разрешить представлять в формате
при минимальном порядке
как нормализованные, так и не нормализованные
числа. Так как порядок на интервале
не изменяется, то плотность распределения
чисел на нем сохраняется неизменной.
Точность представляемых чисел на
интервале [0,![]() ]
будет снижаться до нуля по мере их
приближения к нулю, а точность всех
остальных чисел на интервале
]
будет снижаться до нуля по мере их
приближения к нулю, а точность всех
остальных чисел на интервале
![]() будет одинакова и равна длине поля
мантиссы.
будет одинакова и равна длине поля
мантиссы.
При
![]() в пределах интервала
плотность распределения чисел сохраняется
постоянной. Каждый последующий интервал
в P раз шире предшествующего, и
плотность распределения уменьшается
в P раз. Ширина интервала
растянутой потери значимости составит
в пределах интервала
плотность распределения чисел сохраняется
постоянной. Каждый последующий интервал
в P раз шире предшествующего, и
плотность распределения уменьшается
в P раз. Ширина интервала
растянутой потери значимости составит
![]() часть интервала
часть интервала
![]() ,
на котором порядок
.
,
на котором порядок
.
Например, в десятичной системе счисления, ненормализованные мантиссы имеют 0 в старшем значащем разряде, а нормализованные – цифры от 1 до 9. Следовательно, ненормализованные мантиссы составляют 1/10 часть всех мантисс, и область растянутой потери значимости является 1/10 частью интервала, на котором порядок принимает минимальное значение.
Влияние положения точки в мантиссе
на диапазон представляемых чисел. При
![]() и
и
![]() (в том числе в традиционных системах
счисления с основаниями 2, 8, 10, 16)
максимальная мантисса
(в том числе в традиционных системах
счисления с основаниями 2, 8, 10, 16)
максимальная мантисса
![]() (5-02)
(5-02)
где
– индекс старшего значащего разряда
мантиссы размещенного при
![]() в позиции
;
в позиции
;
– длина поля мантиссы (рис.5-1).
Значение
определяет вес
![]() цифры размещенной в старшей позиции
поля и тем самым положение точки заданной
по умолчанию в поле мантиссы. При
цифры размещенной в старшей позиции
поля и тем самым положение точки заданной
по умолчанию в поле мантиссы. При
![]() точка в мантиссе размещена справа от
позиции
точка в мантиссе размещена справа от
позиции
![]() .
При
.
При
![]() точка размещена слева от позиции
(рис.5-1).
точка размещена слева от позиции
(рис.5-1).
Минимальная нормализованная мантисса
![]() (5-03)
(5-03)
Минимальная ненормализованная мантисса не равная нулю
![]() (5-04)
(5-04)
Следовательно, верхняя граница диапазона
![]() (5-05)
(5-05)
нижняя граница при нормализованной мантиссе
![]() (5-06)
(5-06)
нижняя граница при ненормализованной мантиссе
![]() (5-07)
(5-07)
Из выражений (5-05) – (5-07) следует, что
границы области представляемых чисел
зависят от предельных значений порядка
,
и положения точки в мантиссе
при
![]() .
.
Ничто не препятствует размещению точки далеко за пределами поля мантиссы справа или слева, назначая соответствующий вес старшей позиции или значение индекса .
Можно, выбирая положение точки
,
смещать одновременно все границы
![]() и тем самым смещать область представляемых
чисел на числовой оси по направлению к
нулю или к бесконечности без каких-либо
иных изменений формата. Смещение области
представляемых чисел сопровождается
ее расширением или сужением в зависимости
от направления смещения.
и тем самым смещать область представляемых
чисел на числовой оси по направлению к
нулю или к бесконечности без каких-либо
иных изменений формата. Смещение области
представляемых чисел сопровождается
ее расширением или сужением в зависимости
от направления смещения.
Пример 5-4. Пусть десятичное число
представлено в формате с четырехразрядной
мантиссой и точкой фиксированной справа
от старшего разряда
![]() .
Порядок одноразрядный со знаком
.
Порядок одноразрядный со знаком
![]() ,
,
![]() .
Число +1,23510+4
будет представлено в формате как
0|04|1235, где код знака порядка выделен
жирным шрифтом.
.
Число +1,23510+4
будет представлено в формате как
0|04|1235, где код знака порядка выделен
жирным шрифтом.
В
Таблица 5.2
Ширина диапазона
Точность
0 10 -10
9,99910+9 9,99910+19 9,999×10-1
10-9 10+1 10-19
10-12 10-2 10-22
2×10+10 2×10+20 2
4 4 4
![]()
![]() .
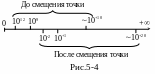
На рис.5-4 показано положение области
чисел представимых в формате.
.
На рис.5-4 показано положение области
чисел представимых в формате.
После смещения точки вправо на
![]() позиций код 0|04|1235 будет представлять
число +123 5000 000010+4
= +1,23510+14. Числу
+1,23510+4= +123 5000
0000×10-6 будет соответствовать код
0|16|1235|.
позиций код 0|04|1235 будет представлять
число +123 5000 000010+4
= +1,23510+14. Числу
+1,23510+4= +123 5000
0000×10-6 будет соответствовать код
0|16|1235|.
После смещения точки на
![]() позиций коду 0|04|1235 будет соответствовать
число +1,23510-6.
Число +1,23510+4
выйдет за пределы диапазона чисел
представимых в новом формате, так как
значение
позиций коду 0|04|1235 будет соответствовать
число +1,23510-6.
Число +1,23510+4
выйдет за пределы диапазона чисел
представимых в новом формате, так как
значение
![]() составит всего лишь 9,99910-1.
составит всего лишь 9,99910-1.
Из сказанного следует, что, изменяя соглашение о положении точки в поле мантиссы без внесения каких-либо иных изменений в формат, можно
смещать область чисел представимых в формате с сохранением точности формата;
выполнять одновременное умножение одного или всех чисел представленных в формате на
 .
.
Это свойство формата можно использовать при конструировании вычислителей.
Влияние области определения порядка
на диапазон представляемых чисел. Из
анализа выражений (5-05), (5-06) и (5-07) следует,
что изменение значения
приводит к смещению верхней границы
диапазона чисел представимых в формате
без изменения точности формата и
положения нижних границ
![]() и
и
![]() .
.
Изменение значения приводит к сужению или расширению области представимых чисел за счет смещения ее нижних границ.
Одновременное изменение значений
и
на одинаковую величину создает эффект
аналогичный смещению точки в мантиссе
на эту же величину. Например, в
примере
5-4, увеличив при
![]() значения
и
на 10, получим:
значения
и
на 10, получим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Такой же результат будет получен при
смещении точки на 10 позиций вправо (см.
табл.5.2 и рис.5-4).
.
Такой же результат будет получен при
смещении точки на 10 позиций вправо (см.
табл.5.2 и рис.5-4).
Последствия смещения точки в мантиссе
на
![]() разрядов можно компенсировать увеличением
границ
,
области определения порядка на величину
разрядов можно компенсировать увеличением
границ
,
области определения порядка на величину
![]() .
Это позволяет выбором значения
отображать область определения порядка
.
Это позволяет выбором значения
отображать область определения порядка
![]() на любую часть числовой оси без внесения
каких-либо изменений в область представимых
чисел. В частном случае можно отобразить
интервал
на любую часть числовой оси без внесения
каких-либо изменений в область представимых
чисел. В частном случае можно отобразить
интервал
![]() на область только положительных или
только отрицательных чисел и представлять
тем самым порядок в поле формата числами
без знака,3
что существенно упростит выполнение
операций с порядками.
на область только положительных или
только отрицательных чисел и представлять
тем самым порядок в поле формата числами
без знака,3
что существенно упростит выполнение
операций с порядками.
Это свойство формата с плавающей точкой может быть использовано при конструировании специализированных и универсальных ЦВМ на этапе выбора форматов представления данных.
Эффективность использования поля мантиссы. Поскольку для обеспечения максимальной точности представления чисел мантиссы нормализуют, то коды поля мантиссы, содержащие 0 в старшей позиции, для хранения чисел не используются. Фактически эти коды являются запрещенными и не несут полезную информацию. Эффективность использования поля мантиссы, будем оценивать отношением количества используемых кодов к их общему числу, выраженному в процентах.
Общее число кодов поля мантиссы равно
![]() .
Например, поле десятичных трехразрядных
мантисс может содержать 103 различных
кодов. Из общего числа кодов не используются
коды, содержащие 0 в старшей позиции. Их
количество составляет
.
Например, поле десятичных трехразрядных
мантисс может содержать 103 различных
кодов. Из общего числа кодов не используются
коды, содержащие 0 в старшей позиции. Их
количество составляет
![]() ,
а количество используемых кодов
,
а количество используемых кодов
![]() .
Следовательно, эффективность использования
кодов поля мантиссы, если не принимать
никаких специальных мер при кодировании,
.
Следовательно, эффективность использования
кодов поля мантиссы, если не принимать
никаких специальных мер при кодировании,
![]() (5-08)
(5-08)
С ростом основания системы счисления доля ненормализованных мантисс сокращается и эффективность использования кодов возрастает. Так при P=2 =50%, при P=16 =93,75%.
При записи десятичных мантисс десятичную цифру обычно представляют четырехразрядным двоичным кодом, причем используют только 10 из 16 возможных комбинаций. Эффективность использования двоичного поля мантиссы при записи двоично-десятичных чисел уменьшается до
![]() (5-09)
(5-09)
При записи шестиразрядных десятичных
мантисс
эффективность использования 24 бит поля
мантиссы составит всего лишь 5,36%. При
![]() эффективность будет 0,2%.
эффективность будет 0,2%.
Это свидетельствует о крайне низкой эффективности формата с плавающей точкой при представлении двоично-десятичных мантисс.
Свойство формата с нормализованным представлением двоичной мантиссы.
Старшая позиция поля нормализованной мантиссы при любом основании P не содержит 0. При нормализованная мантисса всегда содержит 1 в старшем разряде. В иных системах счисления нормализованная мантисса может содержать в старшем разряде разные цифры, но не 0. Это свойство позволяет задавать старший значащий разряд двоичной нормализованной мантиссы по умолчанию, или точнее, выполнять совместное кодирование порядка и старшего разряда мантиссы в поле порядка. В иных системах счисления это нецелесообразно.
При задании старшего разряда двоичной нормализованной мантиссы по умолчанию поле мантиссы будет содержать только младшие ее разряды. В новом представлении код значения 0 во всех битах поля мантиссы означает, что мантисса не равна нулю, а имеет минимальное нормализованное значение 100…0. Вследствие этого возникает задача кодирования значения 0 и ненормализованных чисел с порядком необходимых для создания области растянутой потери значимости. Ее решение возможно путем кодирования порядка равного не одним кодом в поле порядка, а двумя кодами. Первый из них, так же как и все прочие коды порядка, определяет, что в поле мантиссы записан код младших разрядов нормализованной мантиссы с 1 в старшем неявно заданном разряде. Запись второго кода в поле порядка означает, что поле мантиссы содержит код младших разрядов ненормализованной мантиссы с 0 в старшем неявно заданном разряде или код нуля.
Пример 5-5. Пусть для кодирования порядка используется четырехразрядный двоичный код. Пусть код 0000 соответствует при ненормализованной мантиссе, а код 0001 соответствует при нормализованной мантиссе. Иные коды порядка соответствуют другим значениям порядка при нормализованной мантиссе. Пусть 6 битовое поле мантиссы содержит младшие разряды мантиссы, а ее старший разряд в поле мантиссы не представлен.
В первой строке записаны коды чисел в формате с неявно заданным старшим разрядом мантиссы. Во второй строке приведены значения тех же кодов после проявления значения старшего разряда
A B C D E F
00001011010 00000011010 00000000000 00001000000 00001001101 00110001101
0 1011010 0 0011010 0 0000000 0 1000000 0 1001101 0E1001101
В вариантах A-E значение порядка совпадает и равно .
В вариантах A, D, E мантисса
нормализована, т.к. код порядка 0001.
Поэтому в варианте D мантисса имеет
минимально возможное нормализованное
значение
![]() а не 0. В варианте D записано минимально
возможное положительное нормализованное
число
а не 0. В варианте D записано минимально
возможное положительное нормализованное
число
![]() являющееся значением нижней границы
области нормализованных положительных
чисел.
являющееся значением нижней границы
области нормализованных положительных
чисел.
В вариантах B, C мантиссы ненормализованные и их старший разряд равен 0. В варианте C мантисса равна 0. Следовательно, формат содержит код нуля.
В варианте F записано число с порядком
![]() принадлежащее области нормализованных
чисел, так как код порядка не равен 0000.
принадлежащее области нормализованных
чисел, так как код порядка не равен 0000.
Из примера следует, что информация о значении старшего разряда мантиссы в поле мантиссы отсутствует и содержится в коде порядка. В этом состоит совместное кодирование порядка и старшего разряда мантиссы в поле порядка.
В двоичной системе счисления совместное кодирование порядка и старшего разряда мантиссы позволяет сократить длину поля мантиссы на один бит, сохранив точность представления чисел, или увеличить точность на один двоичный разряд, сохранив длину формата. При этом эффективность использования кодов поля мантиссы возрастает с 50% до 100%. Однако область представления порядка и, следовательно, область представления нормализованных чисел сужаются, т.к. для записи значения используются два кода, а не один.
Свойства форматов с переменными
длинами полей порядка и мантиссы.
Различают форматы с переменной
ограниченной и неограниченной длиной
поля
![]() .
Если в форматах с фиксированными длинами
полей их длины задают по умолчанию, то
в форматах с переменной длиной одного
или обеих полей необходимо определять
длину переменного поля в явном виде.
Это можно сделать, например, задавая
длину поля или признак окончания/начала
поля.
.
Если в форматах с фиксированными длинами
полей их длины задают по умолчанию, то
в форматах с переменной длиной одного
или обеих полей необходимо определять
длину переменного поля в явном виде.
Это можно сделать, например, задавая
длину поля или признак окончания/начала
поля.
Формат с переменной неограниченной длиной поля мантиссы позволяет выделять количество позиций равное количеству значащих разрядов в записываемом числе, т.е. записывать число с абсолютной точностью. Но, так как числа могут иметь бесконечно большое число значащих разрядов, например число =3,14… , то формат с неограниченной длиной поля мантиссы в его чистом виде не применяется.
Формат с переменной ограниченной длиной поля мантиссы позволяет задавать требуемую точность представления числа назначением предельной длины поля и экономить позиции при записи “коротких” чисел с количеством значащих разрядов меньшим величины заданного ограничения.
Формат с переменной ограниченной длиной поля порядка позволяет экономить количество позиций в поле порядка при записи чисел с “коротким” значением порядка. Задавая большую предельную длину поля порядка, снижают вероятность ситуаций потери значимости и переполнения. При этом среднестатистическая длина формата будет сравнительно небольшой из-за малой вероятности значений порядка близких к предельному.
Формат с переменной неограниченной длиной поля порядка позволяет экономить количество позиций в поле порядка. Важнейшим свойством такого формата является исключение ситуаций переполнения и потери значимости при записи числа в формат, что существенно упрощает вычисления. В этом состоит весьма ценное преимущество формата с переменной неограниченной длиной поля порядка перед форматами с фиксированным или переменным ограниченным полем порядка.
