Среднее геометрическое и среднее гармоническое

Среднее гармоническое и среднее геометрическое случайной величины - числовые характеристики, используемые в экономических вычислениях.

Средним гармоническим случайной величины, принимающей положительные значения, называется величина .

Например, для непрерывной случайной величины, распределенной равномерно на [a, b],

0 < a < b, среднее гармоническое вычисляется следующим образом:

и .

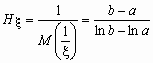Средним геометрическим случайной величины, принимающей положительные значения, называется величина .

Название “среднее геометрическое” происходит от выражения среднего геометрического дискретной случайной величины, имеющей равномерное распределение

 

	a1	a2	a3	...	an
p	1/n	1/n	1/n	...	1/n

 

Среднее геометрическое, вычисляется следующим образом:

,

т.е. получилось традиционное определение среднего геометрического чисел a₁, a₂, …, a_n.

Например, среднее геометрическое случайной величины, имеющей показательное распределение с параметром  , вычисляется следующим образом:

, .

Здесь С  0.577 - постоянная Эйлера.

Наиболее распространенные распределения дискретных случайных величин.

Биномиальное распределение ~ Геометрическое распределение ~ Гипергеометрическое распределение ~ Пуассоновское распределение

 

Биномиальное распределение

Пусть проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. С таким испытанием можно связать случайную величину  , значение которой равно числу успехов в серии из n испытаний. Эта величина принимает значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли

, 0 < p <1, k = 0, 1, …, n, , M = np, D = npq, .

Геометрическое распределение

Со схемой испытаний Бернулли можно связать еще одну случайную величину  - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + и ее распределение определяется формулой

p_k = P(= k) = q^k-1 p, 0 <p <1, k=1, 2, … , , , .

Гипергеометрическое распределение

В партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим. Распределение такой случайной величины называется гипергеометрическим и имеет вид:

, k = 0, 1, …, min(n,M), ,

, .

Пуассоновское распределение

Пуассоновское распределение c параметром  имеет случайная величина  , принимающая целые неотрицательные значения k = 0, 1, 2, … с вероятностями p_k:

, , M =, D =  ,  > 0 - параметр распределения.

 Наиболее распространенные распределения непрерывных случайных величин.

Равномерное распределение ~ Экспоненциальное (показательное) распределение ~ Нормальное распределение ~ Распределение хи-квадрат (c ²- распределение) ~ F-распределение Фишера ~ Распределение Парето ~ Логистическое распределение ~ Логнормальное распределение ~ Вета-распределение ~ Распределение Вейбулла ~ Распределение Коши ~ Гамма-распределение ~ Распределение Лапласа

 

Равномерное распределение

Непрерывная случайная величина  , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_ (x) и функция распределения F_x (x ) имеют соответственно вид:

, .

Экспоненциальное (показательное) распределение

Непрерывная случайная величина  имеет показательное распределение с параметром  > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_ (x )и функция распределения F_ (x) имеют соответственно вид:

, .

Нормальное распределение

Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.

Случайная величина  нормально распределена с параметрами a и  ,  >0, если ее плотность распределения p_ (x ) и функция распределения F_ (x) имеют соответственно вид:

, , M = a, D =  ²_.

Часто используемая запись  ~ N(a,  ) означает, что случайная величина  имеет нормальное распределение с параметрами a и  .

Говорят, что случайная величина  имеет стандартное нормальное распределение, если a = 0 и  = 1 ( ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:

, , M = 0, D = 1.

Здесь - функция Лапласа.

Функция распределения нормальной величины  ~ N(a,  ) выражается через функцию Лапласа следующим образом: .

Если  ~ N(a,  ), то случайную величину  = (x-a)/ называют стандартизованной или нормированной случайной величиной;  ~ N(0, 1) - имеет стандартное нормальное распределение.

 

Распределение хи-квадрат ( ²- распределение)

Пусть  ₁,  ₂, …,  _n - независимые случайные величины, каждая из которых имеет стандартное нормальное распределение N(0, 1). Составим случайную величину

 ² =  ₁² +  ₂² + …+  _n².

Ее закон распределения называется  ²- распределением с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:

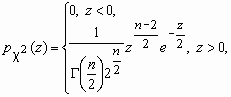
, D 2=2n.

Здесь 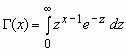- гамма-функция Эйлера.

Распределение Стьюдента

Пусть случайная величина  имеет стандартное нормальное распределение, а случайная величина  _n² -  ²-распределение с n степенями свободы. Если  и  _n² - независимы, то про случайную величину говорят, что она имеет распределение Стьюдента с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:

, x R, M _n = 0, D _n = n/(n-2), n>2.

При больших n распределение Стьюдента практически не отличается от N(0, 1).

F-распределение Фишера

Пусть случайные величины  _n²и  _m² независимы и имеют распределение  ² с n и mстепенями свободы соответственно. Тогда о случайной величине говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:

, x>0, - гамма-функция Эйлера; , m>2; , m > 4.

Распределение Парето

Распределение Парето часто применяется в экономических исследованиях. Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид

, .

Распределение Парето имеет математическое ожидание только при  > 1, а дисперсию - только при  > 2. Cлучайная величина, распределенная по Парето, принимает значения только в области x x₀, x₀ > 0.

Логистическое распределение

Это еще одно распределение, широко применяемое в экономических исследованиях. Для случайной величины  , имеющей логистическое распределение, функция распределения и функция плотности вероятностей имеют соответственно вид:

, ,

, , x R,  и  - параметры распределения.

По своим свойствам логистическое распределение очень похоже на нормальное.

Логнормальное распределение

Случайная величина  имеет логарифмическое нормальное (логнормальное) распределение с параметрами a и  , если случайная величина ln имеет нормальное распределение с параметрами a >и  . Функция распределения и функция плотности вероятностей логнормального распределения имеют соответственно вид:

, , , .

Бета-распределение

Случайная величина  имеет В-распределение (бета-распределение) с параметрами a₁ и a₂, если ее функция плотности вероятностей имеет вид:

Распределение Вейбулла

Случайная величина  имеет распределение Вейбулла с параметрами  ₀ и  , если ее функция распределения и функция плотности вероятностей имеют соответственно вид:

, , , - гамма-функция Эйлера.

Распределение Коши

Случайная величина  имеет распределение Коши с параметрами a и c, если ее функция распределения и функция плотности вероятностей имеют соответственно вид:

У распределения Коши не существует ни математического ожидания, ни дисперсии. Это распределение не имеет ни одного момента положительного порядка.

Гамма-распределение

Случайная величина  имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:

, a > 0, b > 0, , , .

Распределение Лапласа

Случайная величина  имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром  , если ее функция плотности вероятностей имеет вид:

, -

< x <

, M = 0, D = 2/ ^2.

 

Предельные теоремы для биномиального распределения.

Теорема Пуассона ~ Локальная теорема Муавра—Лапласа ~ Интегральная теорема Муавра—Лапласа ~ Теорема Бернулли

 

Если число испытаний n в схеме независимых испытаний Бернулли растет, а вероятность p уменьшается, то точная формула практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).

 

Теорема Пуассона

 

Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и так, что , , то при любых

Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле можно воспользоваться приближенной формулой

, т.е. использовать формулу Пуассона для  = np.

На практике пуассоновским приближением пользуются при npq < 9.

 

Локальная теорема Муавра-Лапласа

Пусть 0< p <1 и величина при n  ограничена. Тогда .

На практике приближением Муавра-Лапласа пользуются при npq > 9.

Точность формулы растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.

 

Интегральная теорема Муавра-Лапласа

 

Пусть 0< p <1, тогда для схемы Бернулли при n  для любых a и b справедлива формула

.

Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

,

где , , - функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

, где , .

Теорема Бернулли

 

Если  - число успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p, 0 < p < 1, то для любого  > 0 справедливо: .

Утверждение теоремы Бернулли означает, что с ростом числа испытаний n относительная частота успехов  /n приближается к вероятности p успеха в одном испытании.

Достаточно часто возникает необходимость установить, сколько нужно произвести испытаний, чтобы отклонение относительной частоты успехов  /n от вероятности p с вероятностью, больше или равной было меньше . Т.е. требуется найти n, для которого справедливо неравенство . Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению , где - решение уравнения . Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!

 

Совместные распределения нескольких случайных величин.

Многомерные случайные величины. Функции распределения многомерных случайных величин ~ Независимость случайных величин ~ Условные распределения случайных величин ~ Условные распределения дискретных случайных величин ~ Условные распределения непрерывных случайных величин

 

В одном и том же случайном эксперименте можно рассматривать не одну, а несколько - n - числовых функций, определенных на одном и том же пространстве элементарных событий. Совокупность таких функций называется многомерной случайной величиной или случайным вектором и обозначается .

Точнее. На вероятностном пространстве заданы случайные величины ; каждому   эти величины ставят в соответствие n-мерный вектор , который называется n-мерным случайным вектором (n-мерной случайной величиной).

 

Многомерные случайные величины. Функции распределения многомерных случайных величин.

 

Функцией распределения случайного вектора или совместным распределением случайных величин называется функция, определенная равенством

,

где .

По известной многомерной функции можно найти распределение каждой из компонент .

Например, если - двумерная случайная величина, имеющая совместное распределение , то распределения компонент и вычисляются соответственно по формулам:

, .

В дальнейшем будем рассматривать двумерные случайные векторы.

Случайный вектор называется непрерывным случайным вектором, если существует такая неотрицательная функция , что для любого прямоугольника   на плоскости вероятность события равна

.

Функция в этом случае называется совместной плотностью распределения.

Легко показать, что .

Если - совместная плотность распределения двумерного случайного вектора , то плотности распределения его компонент определяются равенствами:

и .

Если - дискретный случайный вектор, то совместным распределением случайных величин и чаще всего называют таблицу вида

 

	y1	y2	...	ym
x1	p11	p12	...	p1m
x2	p12	p12	...	p2m
...	...	...	pij	...
xn	pn1	pn2	...	pnm

где и .

По этой таблице можно найти распределения и компонент  и  . Они вычисляются по формулам:

.