Определение свойств бинарного отношения по его матрице

1. Главная диагональ матрицы рефлексивного отношения P всегда состоит из одних единиц, так как , если .

P рефлексивно тогда и только тогда, когда главная диагональ матрицы ||P|| со- держит только единицы.

2. P – симметрично, тогда и только тогда, когда .

P симметрично тогда и только тогда, когда матрица симметрична относительно главной диагонали.

3. P – антисимметрично, тогда и только тогда, когда в матрице 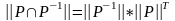все элементы вне главной диагонали являются нулевыми.

P антисимметрично тогда и только тогда, когда матрица вне главной диагонали содержит только нули.

4. P – транзитивно, тогда и только тогда, когда .

P транзитивно тогда и только тогда, когда , где , .

Пример 12. Пусть , , , .

Изобразить графы отношений и , найти матрицу . Проверить с помощью матрицы , является ли отношение рефлексивным, симметричным, транзитивным.

Решение.

Отношение эквивалентности

def. Бинарное отношение на множестве А называется отношением эквивалентности на А, если оно рефлексивно, симметрично и транзитивно (на А).

Отношение эквивалентности часто обозначают символами ~ или ≡.

Пример 13. 1) Отношение равенства на любом множестве чисел.

2) Отношение параллельности на множестве прямых на плоскости.

3) Отношение подобия на множестве треугольников данной плоскости.

Пусть R - отношение эквивалентности на множестве А и .

def. Классом эквивалентности, порождённым элементом 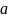, называется множество .

То есть класс эквивалентности, порожденный элементом есть множество всех таких , что . Класс эквивалентности, порождённого элемента , обозначается через /R. Совокупность всех классов эквивалентности отношения R на множестве А обозначается через А/R.

def. Любой элемент класса эквивалентности называется представителем этого класса.

Пусть А - непустое множество.

def. Фактор-множеством множества А по отношению эквивалентности R называется множество A/R всех классов эквивалентности.

def. Разбиением множества А называется такое семейство его непустых подмножеств, объединение которых совпадений с множеством А, а пересечение любых двух различных из них пусто.

Теорема 2 (прямая теорема). Пусть R – отношение эквивалентности на (непустом) множестве А. Тогда фактор – множество A/R является разбиением множества А.

Доказательство.

Следствие. Пусть R – отношение эквивалентности на множестве А, тогда

1. ( Î А) Α Î /R.

2. = A.

3. ( ,b Î А) /R = b/R Û R b.

4. /R ≠ b/R Û /R ∩ b/R = Æ.

Пусть S – разбиение непустого множества А и - бинарное отношение, определяемое следующим образом: (x,y) Î тогда и только, когда x и y принадлежат одному и тому же подмножеству семейства S.

Теорема 3. (обратная теореме 1). Отношение соответствующее разбиению S непустого множества А, является отношением эквивалентности на А, причём фактор- множество А/ совпадает с разбиением S.

Доказательство.

Замечание 3. Частный случай отношения эквивалентности – отношение равенства определяет разбиение множеств на одноэлементные классы эквивалентности

, то есть классов оказывается столько же, сколько элементов содержится в множестве А (каждый элемент из А эквивалентен только самому себе). Другой крайний случай заключается в том, что все элементы А объявляются эквивалентными друг другу, при этом разбиение множества А состоит всего из одного класса – самого множества А. В любом другом случае среди классов разбиения имеется хотя бы один класс, который содержит больше одного элемента и в то же время не совпадает с самим множеством А.

Замечание 4. В чём важность такого разбиения множества на классы? Дело в том, что в каждом классе эквивалентности оказываются эквивалентные элементы, то есть элементы, неразличимы с точки зрения некоторого отношения. Например, равные отрезки или подобные треугольники. Поэтому считают, что класс эквивалентности (множество) определяется любым своим представителем, то есть произвольным элементом этого класса. Так, класс равных отрезков можно задать, указав любой отрезок, принадлежащий этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность отдельных представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, определяется разбиением этого множества на классы треугольников, четырёхугольников, пятиугольников и так далее. Свойства, присущие некоторому классу, рассматриваются на одном его представителе.

Важную роль играют отношения эквивалентности в определении математических понятий.

Пример 14.