Дм. Лекция №6 Тема: «Алгебраические структуры»

Для моделирования кибернетических систем важнейшую роль играют алгебраические структуры. Эти структуры позволяют описывать дискретное строение таких систем и дискретность функционирования таких систем.

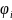def. Множество М вместе с набором операций , M, где n_i - рангом операции , называется алгебраической структурой, универсальной алгеброй или просто алгеброй.

Множество М называется основным (несущим) множеством или основой (носителем); упорядоченная последовательность рангов (n₁,…, n_m) называется типом; множество операций S называется сигнатурой.

Запись: < М ; S > или < М ; >. Операции конечноместны, сигнатура S конечна. Носитель необязательно конечен, но не пуст.

Замечание. Далее для обозначения алгебры везде, где это возможно, используется прописная рукописная буква, а для обозначения ее носителя – соответствующая печатная прописная буква:

А = < A, S >.

def. Алгебры А = < A, f₁, …, f_s > и В = < В,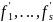 > называются однотипными, если их типы совпадают, то есть ранг операции совпадает с рангом соответствующей ей операции 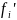для

i = 1,..s.

Примеры.

1. Пусть + и ∙ (сложение и умножение) - арифметические операции на множестве целых чисел. Алгебра < Z,+, ∙ > является алгеброй типа (2,2).

2. Пусть + и ∙ (сложение и умножение) - арифметические операции на множестве натуральных чисел. Алгебра < N,+, ∙ > является алгеброй типа (2,2).

3. Пусть P(U) – множество всех подмножеств непустого множества U и 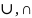,‾ - операции пересечения, объединения и дополнения над подмножествами множества U. Алгебра < P(U), ,‾ > является алгеброй типа (2,2,1).

Алгебры с одной бинарной алгебраической операцией

Рассмотрим алгебры, которые чаще других используются на практике и в теории. Это – полугруппы, моноиды, группы. Пусть А ≠ Æ.

def. Множество с заданной на нем одной ассоциативной бинарной операцией называется полугруппой.

def. Полугруппа с нейтральным элементом называется моноидом.

def. Если заданная бинарная операция еще и коммутативна, то полугруппа, или моноид, называется коммутативной (абелевой).

Итак, в полугруппе может не существовать обратный элемент и даже нейтральный элемент. В моноиде обязательно есть нейтральный элемент, но может не быть обратного.

Пример 1. Рассмотрим множество натуральных чисел с обычной операцией сложения < N,+ >. Это коммутативная (абелевая) аддитивная полугруппа (нет нейтрального элемента).

Пример 2. Множество натуральных чисел с операцией умножения есть коммутативная полугруппа < N,∙ > с нейтральным элементом 1. Здесь есть нейтральный элемент, но нет обратных для всех элементов, не равных единице. Это коммутативный (абелевый) мультипликативный моноид.

def. Алгебра А = < А, > называется группой, если она есть моноид, в котором каждый элемент обратим.

Обратим внимание на то, что в группе есть одна бинарная ассоциативная операция, есть нейтральный элемент и есть симметричный к любому элементу.

Пример 3. Полугруппа < Z,+ > есть аддитивная группа целых чисел. В самом деле, 0 – нейтральный элемент, а симметричный к любому zÎZ является число -n.

Пример 4. Полугруппы < N,+ > и < N,∙ >не являются группами. У первой нет нейтрального элемента, а у второй никакой элемент, кроме 1, не имеет симметричного.

Пример 5. Множество целых чисел относительно умножения < Z,∙ > не образует группу, так как нет обратного для любого элемента множества, кроме единицы.

Пример 6. Все отличные от нуля рациональные числа и все отличные от нуля действительные числа образуют группы относительно умножения (мультипликативные группы), причем коммутативные (абелевые).

Пример 7. Рассмотрим множество 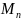квадратных матриц порядка n с элементами из R с определителем, отличным от нуля. Это группа < > относительно операции умножения матриц , поскольку каждый элемент имеет обратный – обратную матрицу. Данная группа – некоммутативная, так как произведение матриц в общем случае некоммутативно.