
- •Дм. Лекция №6 Тема: «Алгебраические структуры»
- •Алгебры с одной бинарной алгебраической операцией
- •Алгебры с двумя бинарными алгебраическими операциями
- •Гомоморфизмы алгебр
- •Булевы алгебры
- •Примеры булевых алгебр
- •Двоичная алгебра логики.
- •Алгебра множеств
- •Алгебра высказываний
- •Алгебра событий
- •Свойства булевой алгебры
- •Алгебраические системы
- •Решетки
Алгебра множеств
Пусть

 ,
P(M)
– булеан
,
P(M)
– булеан

Алгебра высказываний
Пусть
А - множество высказываний относительно
 и
и  .
.
Обозначим через f высказывание, которое всегда ложно и через t высказывание, которое всегда истинно, (f – противоречие, t – тавтология).

 , т.к.
, т.к. 
 ,
т.к. А замкнуто, то
,
т.к. А замкнуто, то

 - алгебра высказываний.
- алгебра высказываний.
Алгебра событий

 , где
, где 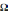
 - пространство элементарных событий,
унарная операция
- пространство элементарных событий,
унарная операция 
 есть операция перехода к противоположному
событию,
есть операция перехода к противоположному
событию, 
 - невозможное событие, и
- достоверное событие.
- невозможное событие, и
- достоверное событие.
Свойства булевой алгебры
Принцип двойственности. Для любой теоремы булевой алгебры, двойственная теорема также верна.
Теорема
1.
Нейтральные элементы
и
относительно + и 
 соответственно единственны.
соответственно единственны.
Теорема
2.
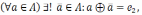
 .
.
Теорема 3. ( Закон идемпотентности).



 .
.
Теорема 4. ( Закон идентичности).

 ,
,

 .
.
Теорема 5. (Закон абсорбции или поглощения)

 ,
,

 .
.
Теорема 6. ( Закон инволюции)

 .
.
Теорема 7. (Законы де Моргана).
 ,
,
 .
.
Теорема
8.

 ,
, 
 .
.
Докажем, например, теорему 7.
Второй закон де Моргана верен по принципу двойственности.
Замечание. Важным приложением булевой алгебры является анализ электронных цепей, связанных с разработкой и проектированием таких цифровых устройств как компьютеры, телефонные системы и электронные системы контроля.
Алгебраические системы
На
непустом множестве 
 ,
наряду с алгебраическими операциями
можно рассматривать и семейство
отношений.
,
наряду с алгебраическими операциями
можно рассматривать и семейство
отношений.
def.
Упорядоченная тройка 
 называется алгебраической
системой,
где
называется алгебраической
системой,
где

 – множество алгебраических операций
на А,
– множество алгебраических операций
на А,

 - множество отношений заданных на
множестве А.
- множество отношений заданных на
множестве А.
Таким образом, алгебры можно считать частным случаем алгебраических систем (в которых множество отношений пусто). Другим частным случаем алгебраических систем являются модели – множества, на которых заданы только отношения. Отношение изоморфизма для алгебраических систем вводится аналогично тому, как это было сделано ранее для алгебр, с той разницей, что к условию сохранения операций добавляется условие сохранения отношений при изоморфизме.
Рассмотрим здесь лишь один пример алгебраической системы, который наиболее часто встречается в теоретической алгебре и её применениях. Этот пример – решётка.
Решетки
def.
Решёткой
называется частичное упорядоченное
множество 


 ,
в котором каждая пара элементов имеет
,
в котором каждая пара элементов имеет

 и
и 
 .
Для заданных элементов
.
Для заданных элементов 
 элемент
элемент 
 называется пересечением
элементов
называется пересечением
элементов

 (обозначается
(обозначается 
 ),
а
),
а 
 называется объединением
элементов
(обозначается
называется объединением
элементов
(обозначается
 ),
таким образом решётка – это алгебраическая
система
),
таким образом решётка – это алгебраическая
система 
 .
.
Отметим,
что операции 
 здесь понимаются как абстрактные
операции алгебраической системы и
отличаются от теоретико-множественных
операций объединения и пересечения,
определенных в алгебре множеств (в
частных случаях могут с ними совпадать).
здесь понимаются как абстрактные
операции алгебраической системы и
отличаются от теоретико-множественных
операций объединения и пересечения,
определенных в алгебре множеств (в
частных случаях могут с ними совпадать).
Решетка – это алгебраическая система

где
- бинарные операции на множестве
,

 - бинарное отношение частичного порядка
на
.
- бинарное отношение частичного порядка
на
.
Заметим, что если в системе введены операции , то отношение можно по этим операциям восстановить следующим образом:

 , а также
, а также

Наименьший (наибольший) элемент решетки, если он существует, называют
нулем (единицей). Обозначаются эти элементы соответственно через 0 и 1. В конечных решетках всегда имеются 0 и 1.
Пример 1. Любое конечное линейно упорядоченное множество является решеткой.
Пример
2.
Рассмотрим 
 ,
в котором
,
в котором 
 ,
а элементы
,
а элементы 
 .
Система
образует решётку, показанную на рисунке
1.
.
Система
образует решётку, показанную на рисунке
1.
В этой решётке a=0, e=1

Пример
3.
Если |
| > 1 , то ч.у.м. 
 не является решеткой, поскольку для
любых различных элементов
не является решеткой, поскольку для
любых различных элементов 
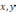 из множества А не определены операции
из множества А не определены операции

 и
по отношению
и
по отношению 
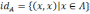 .
.
def.
Решетка

 называется дистрибутивной,
если она подчиняется дистрибутивным
законам, т.е.
называется дистрибутивной,
если она подчиняется дистрибутивным
законам, т.е.





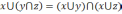 .
.
Не
все решётки являются дистрибутивными.
Решётка, изображенная на рис. 1, не
дистрибутивна, поскольку 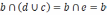
 ,
тогда как
,
тогда как 
 .
.
Дистрибутивная
решётка
называется булевой
алгеброй,
если в
имеется 0 и 1, 
 и
и 

Р



 ешетка
на рис. 2 является дистрибутивной.
ешетка
на рис. 2 является дистрибутивной.



Пример
4.
Рассмотрим множество 
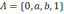 и зададим частичный порядок
на
следующим образом:
и зададим частичный порядок
на
следующим образом: 

Система
является булевой алгеброй, в которой

 ,
,
 .
.
