Раздел 1 . Линейнное программирование

1. Вклад линейного программирования в решение управленческих задач. (постановка транспортной задачи, задачи распределения ресурсов)

Линейное программирование относится к числу наиболее широко распространенных методов, используемых при решении производственных и коммерческих задач. Данный математический аппарат повышает качество планирования, выполняемых фирмой операций, что в значительной степени обуславливает успех дела.

Область применения линейного программирования охватывает производственное планирование, распределение заказов потребителей по различным предприятиям, определение объема денежного обращения, составление графиков комплектования штатов и определение его состава, планирование закупок различного вида сырья и т.д.

Рассмотрим пример построения линейных оптимизационных моделей на примере задачи распределения ресурсов.

1.Задача распределения ресурсов

На предприятии, выпускающем неоднородную продукцию, руководитель стремится определить, какими должны быть уровни производства для каждого продукта в течении некоторого наперед заданного периода. Эти уровни ограничены техническими и другими (внутренними для данного предприятия) условиями. В рамках этих ограничений руководство пытается максимизировать получаемую прибыль.

Предприятие имеет возможность реализовать от одного до четырех различных типов производственно- технологических процессов и обладает правом выбора того или иного варианта. Технологические процессы первого и второго типов ориентированы на получение продукта А, а процессы третьего и четвертого типа продукта В. Расходы, связанные с каждым из технологических процессов, определяются трудозатратами (измеряемыми в человеко - неделях), количество (в единицах веса ) потребляемого в течении недели материала Y и количество (в ящиках ) потребляемого в течении недели материала Z. Затраты, связанные с различными технологическими процессами, не одинаковы, поэтому прибыльность процессов различна даже в том случае, когда они используются для получения продукции одного и того же вида. При составлении производственного плана на неделю диапазон возможностей предпринимателя ограничен как за счет людских ресурсов, так и за счет потребляемого сырья(т.е. материалов Y, Z). Производственные показатели и все имеющиеся ограничения представлены в таблице 1.

таблица 1

	На единицу про-дукции А		На единицу про-дукции В		Имеется в наличии (всего)
	техноло-гичский процесс 1	техноло-гический процесс 2	техноло-гический процесс 3	техноло-гический процесс 4
Количество человеко-недель Количество материала Y в (килограммах) Количество материала Z (единица измерения ящик)	1 7 3	1 5 3	1 3 10	1 2 15	<=15 <=120 <=100
Доход с единицы продукции ( в долларах)	4	5	9	11	Максимизи-ровать
Объем выпускаемой продукции	x1	x2	x3	x4

Для построения линейной оптимизационной модели необходимо учитывать свойства производственно-технологических процессов.

1. Делимость

Для каждого производственно -технологического процесса суммарное количество каждого из потребляемых ресурсов и соответствующая прибыль строго пропорциональны объему выпускаемой продукции, т.е. все показатели производственно -технологического процесса могут быть увеличены или уменьшены при сохранении их взаимной пропорциональности.

2. Аддитивность

Если значение каждой из управляемых переменных xj определено, то полное количество каждого из потребленных ресурсов равняется сумме одноименных ресурсов, затраченных при реализации всех применявшихся технологических процессов, а полная прибыль равняется сумме прибылей, получаемых в результате реализации этих технологических процессов.

Постулирование свойств делимости и аддитивности эквивалентно утверждению о том, что математическая модель может быть представлена в виде линейных соотношений.

В данном примере имеется три линейных неравентсва:

ограничения на трудозатраты;

ограничение на материал Y;

ограничение на материал Z.

Таким образом, линейная модель будет иметь вид:

максимизировать прибыль  максимизировать

(4x1 + 5x2 + 9x3 + 11x4), (1)

при ограничениях

1x1 + 1x2 +1x3 + 1x4 <=15 (человеко-недели) ( 2)

7x1 + 5x2 + 3x3 + 2x4 <=120 (материал Y) (3)

3x1 + 5x2 + 10x3 + 15 x4 <=100 (материал Z) (4)

Отрицательные значения уровней производства не имеют физического смысла, поэтому управляемые переменные xj принимают неотрицательные значения, т.е. xj>=0.

2.Транспортная задача

Некоторый однородный товар имеется на складах поставщиков А1,А2,...,Аm в количествах а1,а2, ... , аm соответственно. С этих складов указанный товар поступает потребителям. Ими являются предприятия B1,B2, ... , bn; потребности которых равны b1,b2, ..., bn единицам соответственно. Перевозка товара по маршруту Ai ---- Bj стоит сij (некоторых денежных средств) за каждую единицу товара.

аi являются запасами поставщиков Аi

bj- потребности потребителей Bj

сij являются тарифами на перевозку груза из Ai в Bj.

Транспортная задача состоит в том, чтобы определить такие объемы xij перевозок товара по маршрутам Ai Bj, чтобы

а)все запасы поставщиков были использованы;

б)все потребности потребителей были удовлетворены;

в)суммарная стоимость перевозок была наименьшей изо всех стоимостей перевозок при всех возможных объемах перевозок xij, удовлетворяющих а), б).

Математическая модель задачи имеет вид:

m n

сij>=0, L(x) =  cij xij.

i=1 j=1

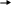cij xij - стоимость перевозки xij товара по маршруту Ai Bj.

Суммирование ведется по всем маршрутам, то есть по всем индексам i= 1,2, ... , m и всем j=1,2, ... , n.

Функция L(x) линейно зависит от набора переменных mn переменных xij; таким образом стоит задача минимизации линейной функции:

mn

L(x) min, xR .

Имеем ограничение xij>=0 при всех i=1, ..., m; j=1,...,n. Кроме того , чтобы все запасы aij были развезены потребителям В1, В2, ... , Вn, сумма перевозок

x1, x2, ... ,xin должна составлять.

x1+ x2+ ... +xn = аi, (*)

условие (*) верно для каждого из поставщиков (при i=1,2, ... ,m).

Чтобы все потребности потребителей Вj были удовлетворены, сумма поставок x1, x2, ... , xjm потребителю Bj от поставщика A1,A2, ... , Am; должна быть равна

x1+ x2+ ... + xjm = bj, (**),

что также справедливо для каждого из потребителей (при j=1, ... ,n).

Система уравнений транспортной задачи, состоящая из m уравнений вида (*) и n уравнений вида (**) , совместна лишь при условии, если

m n

 аi = bj,

i=1 j=1

то есть когда суммарные запасы равны суммарным потребностям. Данная транспортная задача называется замкнутой.