
- •Раздел 1 . Линейнное программирование
- •1. Вклад линейного программирования в решение управленческих задач. (постановка транспортной задачи, задачи распределения ресурсов)
- •2. Алгебраическая формулировка задачи линейного программирования
- •3.Канонические формы для линейных оптимизационных моделей
- •4. Геометрическая интерпритация
- •5.Симплексный метод (решение задачи оптимального распределения ресурсов)
- •6. Анализ моделей на чувствительность и двойственная задача (на примере задачи оптимального распределения ресурсов)
- •Теорема двойственности
- •Следствие теоремы двойственности (Теорема о дополнительной нежесткости)
- •Решение двойственной задачи на примере задачи распределения ресурсов
- •8 Реализация задач линейного программирования средствами ms Excel Реализация задачи распределения ресурсов посредством ms Excel.
- •Анализ оптимального решения
- •Алгоритм решение транспортной задачи с помощью ms Excel.
3.Канонические формы для линейных оптимизационных моделей
Любую задачу линейного программирования можно рассматривать как задачу
n
максимизации cj xj (1)
j=1
при наличии ограничений
n
a ij x j <= b i (i=1,2, ... , m), (2)
j=1
xj >= 0 (i=1,2, ... , n). (3)
Одновременно любую задачу линейного программирования можно свести к
n
минимизации cj xj (4)
j=1
при условии
n
a ij x j = b i ( i=1,2, ... , m), b i >=0 (5)
j=1
xj >= 0 ( i=1,2, ... , n ). (6)
Как правило в (5 ) имеет место неравентсво n>m.
4. Геометрическая интерпритация
Лучшего понимания алгебраических свойств линейных оптимизационных моделей можно добиться с помощью геометрической интерпритации понятий, которые используются в линейном программировании.
Представление в пространстве решений; двумерная задача.
Рассмотрим следующию задачу:
максимизировать 12 x1 +15 x 2 (1)
при наличии ограничений:
4x1 + 3x2 <= 12, (2)
2x1 + 5x2 <= 10, (3)
x1 >= 0, x2 >= 0. (4)
Данная задача графически представлена на рис 1
 x2
x2
 4
4
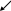
 2
2



 0
0
1 2 3 4 5
рис1 Пространство решений
Поскольку ни одна из этих переменных не может принимать отрицательных значений, область допустимых значений x1 и x2 ограничена, кроме того осями координат. Таким образом, многоугольник Оabc содержит в себе область значений x1 и x2, удовлетворяющих всем имеющимся ограничениям. Множество точек, принадлежащих области ограниченной Оabc (вместе с граничными точками), называется множеством решений. Это множество является выпуклым, т.е. любой отрезок, соединяющий две произвольным образом выбранные точки данного множества, лежит внутри или проходит вдоль границы Оabc. Вершины О, a, b, и c носят название экстремальных точек - они не могут принадлежать внутренней части ни одного из отрезков, соединяющих две различные точки рассматриваемого множества.
Параллельные прямые на рис1 являются графическим изображением различных значений целевой функции. Стрелка, пересекающая эти прямые, направлена в сторону возрастающих значений целевой функции. Оптимальное решение определяется экстремальной точкой b, для которой x1=15/7, x2=8/7, 12x1+1x2=300/7.
Альтернативные оптимальные решения. Если в выражении для целевой функции изменить коэффициенты, то угол наклона параллельных линий по отношению к оси абсцисс будет другим и точка, задающая оптимальное решение переместится.
x2
4
2
0
1 2 3 4 5
рис2 Альтернативные оптимальные решения
Рассмотрим пример. Пусть имеет место некоторое вполне определенное изменение угловых коэффициентов упомянутых выше параллельных прямых, а именно пусть требуется
максимизировать 4x1+10x2 (5)
при наличии тех же самых ограничений (2), (3) и (4).
В этом случае все точки (бесконечное множество точек), лежащие на отрезке ав являются оптимальными. Следовательно предыдущее решение является оптимальным. Но теперь оптимальным является и решение x1=0, x2=2.
Тоже самое можно сказать и о любом положительно - взвешанном среднем двух указанных решений. При этом оптимальное решение целевой функции равно 20.
Неограниченные оптимальные решения. В примере, графически представленом на рис 3, рассматривается следующая модель:
максимизировать -2x1 + 6x2 (6)
при наличии ограничений
-1x1 - 1x2<=-2, (7)
-1x1 + 1x2<=1, (8)
x1>=0,
x2>=0.![]() (9)
(9)
 x2
x2





в


а

рис3 Неограниченное оптимальное решение
Эта задача имеет неограниченное множество решений. Оно выпукло вниз и имеет две экстремальные точки а и b. Для данной задачи значение целевой функции может быть сделано сколь угодно большим, т.е. для любого заданного значения целевой функции решений всегда существует точка, в которой целевая функция принимает еще большее значение. Такая точка лежит на прямой уравнение которой имеет вид -1x1+1x2 = 1 .
Задача не имеющая решения.
Рассмотрим пример: пусть требуется
максимизировать 1x1 +1x2 (10)
при наличии следующих ограничений:
-1x1 +1x2 <= - 1 (11)
1x1 + 1x2 <= - 1 (12)
x1>=0, x2>=0. (13)
Из графика на рис 4 видно, что данная задача не имеет ни одного допустимого решения.


x2





 1
1
0

1
рис 4. Случай, когда не существует оптимального решения
Таким образом, по результатам геометрического рассмотрения приведенных задач можно сделать заключение:
1. Если множество решений является непустым, то оно выпукло и может быть либо ограниченным, либо неограниченным.
2. Если множество решений является непустым, то оптимальное значение целевой функции может быть либо конечным, либо неограниченно большим. В случае когда оптимальное значение целевой функции конечно, оно соответствует экстремальной точке.
