3.2.3.3. Алгоритми побудови тріангуляціїї Делоне

Завдання побудови тріангуляції Делоне є однією з базових в обчислювальній геометрії. До неї зводяться багато інших завдань, вона широко використовується в машинній графіці і геоінформацнонних системах для моделювання поверхонь і рішення просторових задач.

Вперше завдання побудови тріангуляції Делоне була поставлена в 1934 р. в роботі радянського математика Б. Н. Делоне [1]. Її трудомісткість становить O(NlogN) арифметичних операцій. Існують алгоритми, що досягають цієї оцінки в середньому і найгіршому випадках. Крім того, відомі алгоритми, що дозволяють в ряді випадків досягти в середньому O(N). Тим не менш, за цей час багато продовжують працювати над удосконаленням відомих і створенням нових алгоритмів. Це обумовлено нестійкістю ряду відомих алгоритмів і незадовільним часом їх роботи на реальних наборах даних.

Визначення 1. Тріангуляцією називається пленарне розбиття площини на М фігур, з яких одна є зовнішньою нескінченною, а решта – трикутниками.

Визначення 2. Опуклою тріангуляцією називається така тріангуляція, для якої мінімальний полігон, що охоплює всі трикутники, є опуклим. Тріангуляція, що не є опуклою, називається неопуклою.

Визначення 3. Завданням побудови тріангуляції по заданому наборі двовимірних точок називається завдання з'єднання заданих точок непересічними відрізками таким чином, щоб в отриманій тріангуляції між будь-якими двома даними точками не можна було побудувати нові відрізки без перетину з уже існуючими.

Завдання побудови тріангуляції по вихідному набору точок є неоднозначною, тому виникає питання, яка з двох різних тріангуляцій краще. У літературі оптимальною називають таку тріангуляцію, у якій сума довжин всіх ребер мінімальна. При цьому показано [20-22], що задача побудови такої тріангуляції є NP-повною, тобто має складність O(e^N). Тому для більшості практичних задач існуючі алгоритми побудови оптимальної тріангуляції неприйнятні через занадто високу трудомісткість.

Широко відома тріангуляція Делоне, яка не є оптимальною в згаданому сенсі [1, 3, 13, 20, 22], але має ряд інших практично важливих властивостей.

Визначення 4. Кажуть, що тріангуляція задовольняє умові Делоне, якщо всередину кола, описаного навколо будь-якого побудованого трикутника, не потрапляє жодна із заданих точок тріангуляції (рис. 1). Така тріангуляція називається тріангуляцією Делоне.

Рис. 1. Тріангуляція Делоне

Визначення 5. Кажуть, що пара сусідніх трикутників тріангуляції задовольняє умові Делоне, якщо цій умові задовольняє тріангуляція, складена тільки з цих двох трикутників.

Визначення 6. Кажуть, що трикутник тріангуляції задовольняє умові Делоне, якщо цій умові задовольняє тріангуляція, складена тільки із цього трикутника і трьох його сусідів (якщо вони існують).

Багато які алгоритми побудови тріангуляції Делоне використовують наступну теорему [3, 16].

Теорема 1. Тріангуляцію Делоне можна отримати з будь-якої іншої тріангуляції з тієї ж системи точок, послідовно перебудовуючи пари сусідніх трикутників АВС і BCD, не задовольняючих умові Делоне, в пари трикутників ABD і ACD (рис. 2)

Рис. 2. Перебудова трикутників,які не задовольняють умові Делоне.

Таку операцію перебудови часто називають фліпом. Дана теорема дозволяє будувати тріангуляції Делоне послідовно, спочатку будуючи деяку тріангуляцію, а потім послідовно покращуючи її в сенсі умови Делоне. При перевірці умови Делоне для пар сусідніх трикутників можна використовувати безпосередньо визначення, але іноді використовуються інші способи, засновані на наступних теоремах [3, 15, 17, 26].

Теорема 2. Тріангуляція Делоне має максимальну суму мінімальних кутів всіх своїх трикутників серед всіх можливих тріангуляцій.

Теорема 3. Тріангуляція Делоне володіє мінімальною сумою радіусів кіл, описаних біля трикутників, серед усіх можливих тріангуляцій.

У даних теоремах фігурує якась сумарна характеристика всієї тріангуляції (сума мінімальних кутів або сума радіусів), оптимізуючи яку, можна отримати тріангуляцію Делоне.

Тріангуляція Делоне має ряд інших важливих властивостей, що виділяють її серед альтернативних класів тріангуляцій. Зокрема, можна виділити властивість подвійності тріангуляції Делоне діаграмі (розбиття) Вороного [1, 6, 7].

1.1. Структури для подання тріангуляції. Як показує практика, вибір структури для подання тріангуляції має суттєвий вплив на трудомісткість алгоритмів, що використовують дану структуру, а також на швидкість конкретної реалізації. Крім того, структура тріангуляції може залежати від мети її подальшого використання. У тріангуляції можна виділити три основні види об'єктів: вузли (точки, вершини), ребра (відрізки) і трикутники.

У багатьох існуючих алгоритмах побудови тріангуляції Делоне і алгоритмах аналізу тріангуляції часто використовуються наступні операції:

1. Трикутник → вузли: отримання для даного трикутника трьох утворюючих його вузлів.

2. Трикутник → ребра: отримання для даного трикутника списку утворюючих його ребер.

3. Трикутник → трикутники: отримання для даного трикутника списку сусідніх з ним трикутників.

4. Ребро → вузли: отримання для даного ребра координат утворюючих його вузлів.

5. Ребро → трикутники: отримання для даного ребра списку сусідніх з ним трикутників.

6. Вузол → ребра: отримання для даного вузла списку суміжних з ним ребер.

7. Вузол → трикутники: отримання для даного вузла списку суміжних з ним трикутників.

8. Точка → об'єкт тріангуляції: отримання в заданій точці площини вузла, ребра чи трикутника.

У тих чи інших алгоритмах деякі з цих операцій можуть не використовуватися. У деяких алгоритмах операції з ребрами можуть виникати не часто, тому ребра можуть представлятися побічно як одна з сторін деякого трикутника. Розглянемо найбільш часто зустрічаючі в літературі структури.

1.1.1. Структура «Вузли з сусідами». У структурі «Вузли з сусідами» для кожного вузла тріангуляції зберігаються його координати на площині і список вказівників на сусідні вузли (список номерів вузлів), з якими є спільні ребра (рис. 3, 4) [23]. По суті, список сусідів визначає в неявному вигляді ребра тріангуляції. Трикутники ж при цьому не представляються взагалі, що є звичайно істотною перешкодою для подальшого застосування тріангуляції. Крім того, недоліком є змінний розмір структури вузла, часто призводить до неекономної витрати оперативної пам'яті при побудові тріангуляції. Середнє число суміжних вузлів в тріангуляції Делоне дорівнює шість (це доводиться по індукції або із теореми Ейлера про пленарні графи), тому при 8-байтовому поданні координат, 4-байтових цілих і 4-байтових вказівниках сумарний обсяг пам'яті, зайнятий даною структурою, складає 44∙N байт.

Вузол = record

X: число; ← координата Х

Y: число; ← координата Y

Count: ціле; ← кількість суміжних вузлів Делоне

Nodes: array [1 .. Count] of Вказівник_на_вузол; ← список суміжних вузлів

end;

Рис. 3. Структура даних тріангуляції «Вузли з сусідами»

Рис. 4. Зв'язки вузлів структури «Вузли з сусідами»

1.1.2. Структура «Подвійні ребра». У структурі «Подвійні ребра» основою тріангуляції є список орієнтованих ребер. При цьому кожне ребро входить в структуру тріангуляції двічі, але спрямованими в протилежні сторони. Для кожного ребра зберігаються наступні вказівники (рис. 5,6) [14]:

1) на кінцевий вузол ребра;

2) на наступне за годинниковою стрілкою ребро в трикутнику, що знаходиться праворуч від даного ребра;

3) на «ребро-близнюк», що з'єднує ті ж самі вузли тріангуляції, що і дане, але спрямоване в протилежну сторону;

4) на трикутник, що знаходиться праворуч від ребра.

Останній вказівник не потрібен для побудови тріангуляції, і тому його наявність має визначатися в залежності від мети подальшого застосування тріангуляції.

Недоліками даної структури є представлення трикутників в неявному вигляді, а також велика витрата пам'яті, що становить при 8-байтовому поданні координат і 4-байтових вказівниках не менше 64∙N байт (не враховуючи витрати пам'яті на подання додаткових даних в трикутниках).

1.1.3. Структура «Вузли, ребра і трикутники». У структурі «Вузли, ребра і трикутники» в явному вигляді задаються всі види об'єктів тріангуляції: вузли, ребра і трикутники. Для кожного ребра

Вузол = record

X: число; ← координата X

Y: число; ← координата Y

end;

Ребро = record

Mode: Вказівник_на_вузол; ← кінцевий вузол ребра

Next: Вказівник_на_ребро; ← наступне за годинниковою стрілкою ребро в трикутнику праворуч

Twin: Вказівник_на_ребро; ← таке ж ребро (близнюк), але спрямоване в іншу сторону

Triangle: Вказівник_на_трикутник; ← вказівник на трикутник праворуч

end;

Трикутник = record

end;

Рис. 5. Структура даних тріангуляції «Подвійні ребра»

Рис. 6. Зв'язки ребер (ліворуч) і неявне подання трикутників (праворуч) у структурі «Подвійні ребра»

зберігаються вказівники на два кінцевих вузла і два сусідніх трикутника. Для трикутників зберігаються вказівники на три утворюючих трикутник ребра (рис. 7, 8) [11].

Недоліком цієї структури є велика витрата пам'яті, що становить при 8-байтовому поданні координат і 4-байтових вказівниках приблизно 88∙N байт.

Вузол = record

X: число; ← координата Х

Y: число; ← координата Y

end;

Ребро = record

Modes: array [1 .. 2] of Вказівник_на_вузол; ← список кінцевих вузлів

Triangles: array [1 .. 2] of Вказівник_на_трикутник; ← список сусідніх трикутників

end;

Трикутник = record

Ribs: array [1 .. 3] of Вказівник_на_ребро; ← список утворюючих ребер

end;

Рис. 7. Структура даних тріангуляції «Вузли, ребра і трикутники»

Рис. 8. Зв'язки трикутників (ліворуч) і ребер (праворуч) структури «Вузли, ребра і трикутники»

1.1.4. Структура «Вузли й трикутники». У структурі «Вузли й трикутники» для кожного трикутника зберігаються три вказівника на утворюючі його вузли і три вказівника на суміжні трикутники (рис. 9, 10) [9, 18, 25]. Нумерація точок і сусідніх трикутників проводиться в порядку обходу за годинниковою стрілкою, при цьому навпроти точки з номером і€{1,2,3} розташовується ребро, відповідне сусідньому трикутнику з таким же номером. Ребра в цій тріангуляції в явному вигляді не зберігаються. При необхідності ж вони зазвичай представляються як вказівник на трикутник і номер ребра усередині нього. При 8-байтовому поданні координат і 4-байтових вказівниках потрібно приблизно 40∙N байт. Дана структура тріангуляції найбільш часто застосовується на практиці в силу своєї компактності і відносній зручності в роботі.

Вузол = record

X: число; ← координата Х

Y: число; ← координата Y

end;

Трикутник = record

Nodes: array [1 .. 3] of Вказівник_на_вузол; ← список утворюючих вузлів

Triangles: array [1 .. 3] of Вказівник_на_трикутник; ← список суміжних треугольників

end;

Рис. 9. Структура даних тріангуляції «Вузли і трикутники»

Рис. 10. Зв'язки трикутників структури «Вузли й трикутники»

1.2. Перевірка умови Делоне. Одна з найважливіших операцій, які виконуються при побудові тріангуляції, є перевірка умови Делоне для заданих пар трикутників. На основі визначення тріангуляції Делоне і теореми 2 на практиці зазвичай використовують декілька способів перевірки.

1. Перевірка через рівняння описаного кола.

2. Перевірка з раніше обчисленим описаним колом.

3. Перевірка суми протилежних кутів.

4. Модифікована перевірка суми протилежних кутів.

1.2.1. Перевірка через рівняння описаного кола. Рівняння кола, що проходить через точки (х₁,у₁), (х₂,у₂), (х₃,у₃) можна записати в такому вигляді:

Інший запис рівняння цього кола має вигляд (х²+у²)∙a – x∙b + y∙c – d = 0, де

Тоді умова Делоне для Δ((х₁,у₁), (х₂,у₂), (х₃,у₃)) виконується тільки тоді, коли для будь-якої іншої точки (х₀, у₀) тріангуляції справедлива нерівність (а∙( ) – b∙x₀ + c∙y₀ – d)∙sgn a ≥ 0, тобто коли точка (х₀, у₀) не потрапляє всередину кола, описаного навколо Δ((х₁,у₁), (х₂,у₂), (х₃,у₃)) [12]. Для спрощення обчислень можна помітити, що якщо трійка точок (х₁,у₁), (х₂,у₂), (х₃,у₃) є правою, то завжди sgn a = -1, і навпаки, якщо трійка ця ліва, то sgn a = 1.

Безпосередня реалізація такої процедури перевірки вимагає 29 операцій множення і зведення в квадрат, а також 24 операції додавання і віднімання.

1.2.2. Перевірка з раніше обчисленим описаним колом. Попередній варіант перевірки вимагає значної кількості арифметичних операцій. Тим не менш, в більшості алгоритмів тріангуляції кількість перевірок умови багаторазово (у різних алгоритмах ця цифра коливається від 2 до 25 і більше) перевищує загальне число різних трикутників, присутніх в тріангуляції на різних кроках її побудови. Тому основна ідея алгоритму перевірки через раніше обчислені кола полягає в попередньому обчисленні для кожного побудованого трикутника центру і радіусу описаного навколо нього кола, після чого перевірка умови Делоне буде зводитися до обчислення відстані до центру цього кола і порівнянню результату з радіусом. Центр (х_с, у_с) і радіус r кола, описаного навколо Δ((х₁,у₁), (х₂,у₂), (х₃,у₃)) можна знайти як х_с = b/2а, уc = -с /2а, r² = (b² + с² - 4ad)/4a², де значення а, b, с, d визначені вище в (1).

Тоді умова Делоне для Δ((х₁,у₁), (х₂,у₂), (х₃,у₃)) буде виконуватися тільки тоді, коли для будь-якої іншої точки (x₀,y₀) тріангуляції буде (x₀ – x_c )² + (у₀ – y_c )² ≥ r².

Реалізація такої процедури перевірки вимагає для кожного трикутника 36 операцій множення, зведення в квадрат і ділення, а також 22 операції додавання і віднімання. На етапі безпосереднього виконання перевірок потрібно всього лише два зведення в квадрат, два віднімання, одне додавання і одне порівняння. Якщо прийняти, що алгоритм тріангуляції витрачає в середньому по п'ять перевірок на кожен трикутник, то в середньому даний спосіб перевірки вимагає близько дев'яти операцій типу множення і сім операцій типу додавання. Якщо алгоритм витрачає в середньому по 12 перевірок на кожен трикутник, то кількість операцій зменшується відповідно до шести і шести. Точна ж оцінка середнього числа операцій повинна виконуватися для конкретного алгоритму тріангуляції і типових видів вихідних даних.

1.2.3. Перевірка суми протилежних кутів. В [12, 24] показано, що умова Делоне для трикутника Δ((х₁,у₁), (х₂,у₂), (х₃,у₃)) буде виконуватися тільки тоді, коли для будь-якої іншої точки (x₀,y₀) тріангуляції буде α + β ≤ π (рис. 11).

Ця умова еквівалентна sin (α + β) ≥ 0, тобто

sinα ∙ cosβ + cosα ∙ sinβ ≥ 0.

Рис. 11. Перевірка суми протилежних кутів

Значення синусів і косинусів кутів можна обчислити через скалярні і векторні добутки векторів:

Підставивши ці значення в формулу (2) і скоротивши знаменники дробів, отримаємо наступну формулу перевірки:

Безпосередня реалізація такої процедури перевірки вимагає 10 операції множення, а також 13 операцій додавання і віднімання.

1.2.4. Модифікована перевірка суми протилежних кутів. В [24] запропоновано обчислювати не відразу всі скалярні і векторні добутки. Спочатку потрібно визначити лише ті вирази в (3), які відповідають cos α і cosβ:

Якщо s_α < 0 і s_β < 0, то α > 90 ° і β > 90 ° (Делоне не виконується), а якщо s_α ≥ 0 і s_β ≥ 0, то α ≤ 90 ° і β ≤ 90 ° (умова Делоне виконується); інакше потрібні повні обчислення за формулою (3). Таке удосконалення дозволяє в середньому на 20-40% (істотно залежить від алгоритму тріангуляції) скоротити кількість виконуваних арифметичних операцій (приблизно до семи множень і до дев'яти додавань і віднімань).

2. Ітеративні алгоритми. Всі ітеративні алгоритми мають в своїй основі ідею послідовного додавання точок у частково побудовану тріангуляцію Делоне. Формально цей процес може бути описаний так.

Нехай є тріангуляція Делоне на безлічі з ( n –1) точок. Чергова n-а точка додається у вже побудовану структуру тріангуляції наступним чином.

Крок 1. Спочатку здійснюється локалізація точки, тобто знаходиться трикутник (збудований раніше), в який потрапляє чергова точка. Якщо точка не потрапляє всередину тріангуляції, то знаходиться трикутник на границі тріангуляції, найближчий до чергової точки.

Крок 2. Якщо точка потрапила на раніше вставлений вузол тріангуляції, то така точка зазвичай відкидається, інакше точка вставляється в тріангуляцію у вигляді нового вузла. При цьому, якщо точка потрапила на деяке ребро, то воно розбивається на два нових, а обидва суміжних з ребром трикутника також діляться на два менших. Якщо точка потрапила суворо всередину якого-небудь трикутника, він розбивається на три нових. Якщо точка потрапила поза тріангуляції, то будується один або більше трикутників. Потім проводяться локальні перевірки знову отриманих трикутників на відповідність умові Делоне і виконуються необхідні перебудови.

Складність даного алгоритму складається з трудомісткості пошуку трикутника, в який на черговому кроці додається точка, трудомісткості побудови нових трикутників, а також трудомісткість відповідних перебудов структури тріангуляції в результаті незадовільних перевірок пар сусідніх трикутників отриманої тріангуляції на виконання умови Делоне.

При побудові нових трикутників можливі дві ситуації: додана точка потрапляє або в середину тріангуляції, або поза нею. В першому випадку будуються нові трикутники і число виконуючих алгоритмом дій фіксовано. У другому – необхідна побудова додаткових зовнішніх до поточної тріангуляції трикутників, причому їх кількість може в гіршому випадку дорівнювати n – 3. Однак за всі кроки роботи алгоритму буде додано не більше 3∙ N трикутників, де N - загальне число вихідних точок. Тому в обох випадках загальний витрачений час на побудову трикутників становить О(N).

Щоб трохи спростити алгоритм, можна взагалі позбавитися від другого випадку, попередньо внісши в тріангуляцію кілька таких додаткових вузлів, що побудована на них тріангуляція завідомо накриє всі вихідні точки тріангуляції. Така структура зазвичай називається суперструктурою. На практиці для суперструктури зазвичай вибирають такі варіанти (рис. 12):

а) вершини рівностороннього трикутника, що покриває всю безліч вихідних точок;

б) вершини квадрата, що покриває всю безліч вихідних точок;

(а) (б) (в) (г) (д)

Рис. 12. Варіанти суперструктур

в) θ(√N) точок, рівномірно розподілених по колу, що покриває всю безліч вихідних точок;

г) θ(√N) точок, рівномірно розподілених по квадрату, що покриває всю безліч вихідних точок;

д) вихідні точки, що потрапляють на опуклу оболонку множини вихідних точок.

В [8] наводяться результати експериментального порівняння різних варіантів суперструктур. При цьому показується, що при використанні суперструктури на різних розподілах вихідних даних можливе як збільшення швидкості роботи алгоритмів, так і її зниження, але не більше ніж на 10%.

Будь-яке додавання нової точки в тріангуляцію теоретично може порушити цілісність умови Делоне, тому після додавання точки зазвичай відразу ж проводиться локальна перевірка тріангуляції на умову Делоне. Ця перевірка повинна охопити всі новозбудовані трикутники і сусідні з ними. Кількість таких перебудов в гіршому випадку може призвести до повного перебудування всієї тріангуляції, тому трудомісткість перебудов становить О(N). Проте середнє число таких перебудов на реальних даних складає лише близько трьох [8].

Таким чином, найбільший внесок у трудомісткість ітеративного алгоритму дає процедура пошуку чергового трикутника. Саме тому все ітеративні алгоритми побудови тріангуляції Делоне відрізняються один від одного головним чином тільки процедурою пошуку чергового трикутника.

2.1. Простий ітеративний алгоритм. У простому ітеративному алгоритмі пошук чергового трикутника реалізується наступним чином. Береться будь-який трикутник, який вже належить тріангуляції (наприклад, вибирається випадково), і послідовними переходами по зв'язаних трикутниках шукається шуканий трикутник.

При цьому в гіршому випадку доводиться перетинати всі трикутники тріангуляції, тому трудомісткість такого пошуку складає О(N). Однак у середньому для рівномірного розподілу в квадраті потрібно зробити тільки O(√N) операцій переходу [25]. Таким чином, трудомісткість найпростішого ітеративного алгоритму складає в гіршому випадку О(N²)., а в середньому – О(N^3/2). [15, 18].

У багатьох практично важливих випадках вихідні точки не є статистично незалежними, при цьому і-а точка знаходиться поблизу (і+1)-й. Тому в якості початкового трикутника для пошуку можна брати трикутник, знайдений раніше для попередньої точки. Тим самим іноді вдається досягти на деяких видах вихідних даних трудомісткості побудови тріангуляції в середньому О(N).

(а) (б) (в)

Рис. 13. Варіанти локалізації трикутника в ітеративних алгоритмах.

На практиці звичайно використовуються наступні способи пошуку трикутника за заданою точкою в середині нього і по деякому вихідного трикутнику (рис. 13).

1. Проводиться пряма через деяку точку всередині вихідного трикутника і цільову точку. Потім пошук здійснюється вздовж цієї прямої до мети [15]. При цьому необхідно коректно обробляти ситуації, коли на шляху можуть зустрітися вузли і колінеарні ребра.

2. Рухатися по одному кроку, на кожному кроці проводячи пряму через центр поточного трикутника і цільову точку, і потім переходячи до сусіднього трикутника, відповідного стороні, яку перетинає побудована пряма [18].

3. Рухатися по одному кроку, на кожному із яких треба переходити через таке ребро поточного трикутника, що цільова точка і вершина поточного трикутника, протилежна обраному пересічному ребру, лежать по різні сторони від прямої, яка визначається даними ребром [8]. Цей спосіб звичайно дає більш довгий шлях до мети, але він алгоритмічно простіше і тому швидше. Для правильної роботи даного алгоритму пошуку істотним є те, що в тріангуляції виконується умова Делоне. Якщо умова Делоне порушена, то іноді можливе зациклення алгоритму.

Після того як необхідний трикутник знайдений, в ньому будуються нові вузли, ребра і трикутники, а потім проводиться локальне перебудовування тріангуляції.

2.1.1. Ітеративний алгоритм «Видаляй і будуй». У ітеративному алгоритмі «Видаляй і будуй» не виконується ніяких перебудов. Замість цього при кожній вставці нового вузла (рис. 14 а) відразу ж віддаляються всі трикутники, у яких всередину описаних кіл потрапляє новий вузол (рис. 14б). При цьому всі видалені трикутники неявно утворюють певний полігон. Після цього на місці вилучених трикутників будується заповнююча тріангуляція шляхом з'єднання нового вузла з цим полігоном (рис. 14в) [27].

(а) (б) (в)

Рис. 14. Вставка точки в ітеративному алгоритмі «Видаляй і будуй»

Даний алгоритм будує відразу всі необхідні трикутники на відміну від звичайного ітеративного алгоритму, де при вставці одного вузла можливі багаторазові перебудови одного і того ж трикутника. Проте тут на перший план виходить процедура виділення контуру віддаленого полінома, від ефективності роботи якого залежить загальна швидкість алгоритму. В цілому, в залежності від використовуваної структури даних цей алгоритм може витрачати часу менше, ніж алгоритм з перебудування, і навпаки.

Трудомісткість даного алгоритму повністю збігається з оцінками для простого ітеративного алгоритму.

2.2. Алгоритми з індексуванням пошуку трикутників. В алгоритмах з індексуванням пошуку всі раніше побудовані трикутники заносяться в деяку структуру, за допомогою якої можна досить швидко знаходити трикутники в заданій точці площині.

2.2.1. Ітеративний алгоритм з індексуванням трикутників. В алгоритмі тріангуляції з індексуванням трикутників для всіх побудованих трикутників обчислюється мінімальний осяжний прямокутник зі сторонами, паралельними осям координат, і заноситься в R-дерево [13].

При видаленні старих трикутників необхідно їх видаляти з R-дерева, а при побудові нових – заносити.

Для виконання пошуку трикутника, в який потрапляє поточна вставлена в тріангуляцію точка, необхідно виконати стандартний точковий запит до R-дерева та отримати список трикутників, чиї осяжні прямокутники знаходяться в даній точці. Потім треба вибрати з них той трикутник, всередину якого потрапляє точка.

Зазначимо, що структура R-дерева не дозволяє знайти об'єкт, найближчий до заданої точки. Саме тому даний алгоритм тріангуляції з використанням R-дерева слід застосовувати тільки з суперструктурою, щоб виключити потрапляння чергової точки поза тріангуляцію.

Трудомісткість пошуку трикутника в R-дереві в гіршому випадку становить О(N), а в середньому – О(log N). При цьому може бути знайдено від одного до N трикутників, які треба потім все перевірити. Крім того, виникають додаткові витрати часу на підтримку структури дерева: О(log N) при кожній побудові і видаленні трикутників. Звідси отримуємо, що трудомісткість алгоритм тріангуляції з індексуванням трикутників в гіршому випадку становить О(N²), а в середньому – О(N log N).

2.2.2. Ітеративний алгоритм з індексуванням центрів трикутників k-D-деревом. В алгоритмі тріангуляції з індексуванням центрів трикутників k-D-деревом в дерево [13] розміщуються тільки центри трикутників. При видаленні старих трикутників необхідно видаляти їх центри з k-D-дерева, а при побудові нових – заносити.

Для виконання пошуку трикутника, в який потрапляє поточна вставлена в тріангуляцію точка, необхідно виконати нестандартний точковий запит до k-D-дерева. Пошук в дереві необхідно починати з кореня і спускатися вниз до листя. У разі якщо нащадки поточного вузла k-D-дерева (охоплюючий нащадки прямокутник) не покривають поточну точку, то необхідно вибрати для подальшого спуску по дереву нащадка, найближчого до точки пошуку.

В результаті буде знайдено певний трикутник, центр якого буде близький до заданої точки. Якщо в знайдений трикутник не потрапляє задана точка, то далі необхідно використовувати звичайний алгоритм пошуку трикутника з простого ітеративного алгоритму побудови тріангуляції Делоне.

Трудомісткість пошуку точки в k-D-дереві в гіршому випадку становить О(N), а в середньому – О(log N). Далі може бути задіяна процедура переходу по трикутниках з трудомісткістю О(N) в гіршому випадку. Додаткові витрати часу на підтримку структури дерева оцінюються як О(log N) при кожній побудові і видаленні трикутників. Звідси отримуємо, що трудомісткість алгоритму тріангуляції з індексуванням трикутників в гіршому випадку становить О(N²), а в середньому – О(N log N).

2.2.3. Ітеративний алгоритм з індексуванням центрів трикутників квадродеревом. При використанні цього алгоритму в дерево також поміщаються тільки центри трикутників [6, 13]. В цілому робота алгоритму і оцінка трудомісткості збігається з попереднім алгоритмом тріангуляції. Однак на відміну від алгоритму з k-D-деревом квадродерево більш просте в реалізації і дозволяє більш точно знаходити найближчий трикутник. У той же час, на нерівномірних розподілах квадродерево поступається k-D-дереву.

2.3. Алгоритми з кешуванням пошуку трикутників. Алгоритми тріангуляції з кешуванням пошуку декілька схожі на алгоритми тріангуляції з індексуванням центрів трикутників. При цьому будується кеш-спеціальна структура, яка дозволяє за час О(1) знаходити певний трикутник, близький до шуканого. На відміну від алгоритмів тріангуляції з індексуванням змінені трикутники з кешу не видаляються (передбачається, що кожен віддалений трикутник як запис в пам'яті комп'ютера перетворюється в новий трикутник і тому допустимість посилань на трикутники не порушується при роботі алгоритму), один і той самий трикутник може багаторазово перебувати в кеші, а деякі трикутники можуть бути взагалі там відсутні [8].

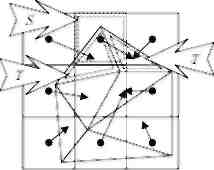
Рис. 15. Локалізація точок в кеші (S - знайдений квадрат, Т’ - пов'язаний з квадратом трикутник, Т - кінцевий трикутник)

Основна ідея кешування полягає в побудові деякого більш простого пленарного розбиття площини, ніж тріангуляція, в якому можна швидко виконувати локалізацію точок. Для кожного елемента простого розбиття робиться посилання на трикутник тріангуляції. Процедура пошуку зводиться до локалізації елемента простого розбиття, переходу за посиланням до трикутника і подальшої локалізації шуканого трикутника алгоритмом з простого ітеративного алгоритму тріангуляції Делоне. В якості такого розбиття найпростіше використовувати регулярну мережу квадратів (рис. 15). Наприклад, якщо дане пленарне розбиття повністю покривається квадратом [0; 1] х [0, 1], то його можна розбити на m² рівних квадратів. Занумеруем їх усіх природним чином двома параметрами i, j = . Тоді по даній точці (х, у) ми можемо знайти квадрат [х/ т], [у / т], де [...]-знак взяття цілої частини числа.

КЗШ у вигляді регулярної мережі квадратів найбільш добре працює для рівномірного розподілу вихідних точок і розподілів, що не мають високих піків у функції щільності. У разі ж якщо заздалегідь відомий характер розподілу, можна вибрати якесь інше розбиття площині (наприклад, у вигляді нерівномірно віддалених вертикальних і горизонтальних прямих).

2.3.1. Ітеративний алгоритм зі статичним кешуванням пошуку. В алгоритмі тріангуляції зі статичним кешуванням пошуку необхідно вибрати число т і завести кеш у вигляді двовимірного масиву r розміром т х т для посилань на трикутники [8]. Спочатку цей масив треба заповнити посиланнями на самий перший побудований трикутник. Потім, після виконання чергового пошуку, в якому був знайдений певний трикутник Т, починаючи пошук із квадрата (i, j), необхідно обновить інформацію в кеші: r_i,j: = посилання на Т. Розмір статичного кеша слід вибирати за формулою т = s ∙ N^3/8, де s-коефіцієнт статичного кеша. На практиці значення s слід взяти ≈ 0,6 - 0,9.

Перший час, поки кеш не оновиться повністю, пошук може йти досить довго, але потім швидкість підвищується. Цього недоліку позбавлений наступний алгоритм.

2.3.2. Ітеративний алгоритм з динамічним кешуванням пошуку. В алгоритмі тріангуляції з динамічним кешуванням пошуку необхідно завести кеш мінімального розміру, наприклад 2x2. В міру зростання числа доданих в тріангуляцію точок необхідно послідовно збільшувати його розмір у два рази, переписуючи при цьому інформацію з старого кеша в новий. При цьому для збільшення кеша треба виконати наступні пересилання (r - старий кеш, r'- новий): i, j = : r`<sub>2i,2j</sub> ,r`_2i,2j+1,r`<sub>2i+1,2j</sub>,r`_2i+1,2j+1: = r_i,j Даний алгоритм кешування дозволяє однаково ефективно працювати на малій і великій кількості точок, заздалегідь не знаючи їх числа.

Збільшення розміру динамічного кешу в два рази слід проводити кожного разу при досягненні числа точок в тріангуляції п = r∙т², де r - коефіцієнт зростання динамічного кешу, а т - поточний розмір кеша. На практиці значення коефіцієнта зростання динамічного кешу слід вибрати ≈ 3-8.

Трудомісткості алгоритмів тріангуляції з кешуванням як і всіх ітеративних алгоритмів становить в гіршому випадку О(N²), а в середньому на рівномірному розподілі для статичного кешування – О(N^9/8) та для динамічного кешування – О(N) [8].

Для більшості випадкових розподілів вихідних точок даний алгоритм працює значно швидше за всі інші алгоритми. Однак на деяких реальних даних, в яких послідовні вихідні точки знаходяться поблизу один одного (наприклад, точки ізоліній карт рельєфу), алгоритм динамічного кешування може витрачати більше часу, ніж інші алгоритми. Для обліку такої ситуації в алгоритм слід додати додаткову перевірку. Якщо чергова додана точка знаходиться від попередньої точки на відстані більшій, ніж деяке число Δ (порядку поточного розміру клітини кешу), то пошук необхідно розпочати з трикутника із кешу, інакше потрібно почати з останнього побудованого трикутника. У такій модифікації алгоритм динамічного кешування стає неперевершеним за швидкістю роботи на більшості реальних даних.

2.4. Ітеративні алгоритми зі зміненим порядком додавання точок. В [15] пропонується змінити порядок додавання точок так, щоб кожна наступна точка була максимально близька до попередньої доданої точки. Тоді, запам'ятовуючи трикутник, знайдений на попередній ітерації, можна використовувати його в якості відправної точки для поточного пошуку, використовуючи алгоритм пошуку з простого ітеративного алгоритму. Вдало перебудовуючи порядок додавання точок, можна досягти дуже непоганих результатів. Однак при цьому на перший план може вийти трудомісткість цієї попередньої обробки.

2.4.1. Ітеративний смуговий алгоритм. У ітеративному смуговому алгоритмі тріангуляції потрібно розбити всі точки на смуги по одній координаті, а потім відсортувати всі точки всередині смуг по іншій координаті [8]. У цьому випадку, підібравши відповідну кількість смуг, можна істотно зменшити відстань між послідовністю точок (рис. 16). В [4] теоретично визначена оптимальна кількість смуг т = [√bN/3a] для розбиття точок на смуги при рівномірному незалежному розподілі точок у прямокутнику розміром b x а, виходячи з умови мінімізації сумарної загальної відстані між послідовними точками розбиття. У даній оцінці, на жаль, не врахований час, що витрачається на попередню обробку – розбиття на смуги. Тому на практиці число смуг краще вибирати все ж у кілька разів менше, ніж наведена оцінка, за формулою = [√sbN / а], де s - константа розбиття на смуги ітеративного смугового алгоритму. При цьому значення s слід вибирати ≈ 0,15 - 0,19.

Рис. 16. Смуговий ітеративний алгоритм.

Трудомісткість даного алгоритму становить в гіршому випадку О(N²), а в середньому при використанні алгоритму сортування з лінійною складністю (наприклад, цифрове сортування) - О(N)

2.4.2. Ітеративний квадратний алгоритм. У ітеративному квадратному алгоритмі тріангуляції [8, 18] необхідно розбити площину з точками на О(√N) квадратів, а додавання точок проводити послідовними групами, відповідним суміжним квадратам (рис. 17).

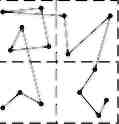
Рис. 17. Квадратний ітеративний алгоритм

В [18] розбиття проводиться на √N квадратів; трудомісткість такого алгоритму складає в гіршому випадку О(N²), а в середньому – О(N^3/2).

В [8] розбиття проводиться на т х т квадратів, де т =[ √sN]. Значення s слід вибирати ≈ 0,004-0,006. При цьому трудомісткість такого алгоритму складає в гіршому випадку О(N²), а в середньому - О(N). На практиці даний алгоритм працює трохи швидше, ніж попередній (приблизно на 10 - 20%) [8].

2.4.3. Ітеративний алгоритм з пошаровим згущенням. В ітеративному алгоритмі тріангуляції з пошаровим згущенням необхідно розбити площину з точками на п = (2^v+1)x(2^v+1) елементарних осередків квадратів однакового розміру. Кожен квадрат нумерується від 0до 2^v по вертикалі і від 0до 2^v по горизонталі Далі вводиться поняття шару. Вважається, що точка належить шару i, якщо обидва номери її квадрата кратні 2ⁱ (тоді всі вихідні точки утворюють шар 0, шар i + 1 буде підмножиною шару i, а максимальний номер шару k = min (u, v)). За значеннями пар номерів всі точки шару i діляться на чотири підмножини:

1) кутові точки (обидва їхні номери кратні 2^і+1) - це шар і+1;

2) внутрішні точки (обидва їхні номери не кратні 2^і+1);

3).Х - граничні точки (тільки номер по координаті. Х кратний 2^і+1);

4) Y-граничні точки (тільки номер по координаті Y кратний 2ⁱ⁺¹).

Додавання точок у тріангуляцію треба проводити пошарово від шару з максимальним номером до нульового. Всередині шару потрібно спочатку внести всі точки другого типу, потім третього і в кінці - четвертого.

На рис. 18 наведено приклад розбиття площини на квадрати при u = 3, v = 2 і п = 9 ∙ 5 по етапах:

а) усі точки шару 1;

б) внутрішні точки шару 0;

в). Х - граничні точки шару 0;

г) Y - граничні точки шару 0.

Рис. 18. Порядок вибору точок в ітеративному алгоритмі з пошаровим згущенням

На рис. 18 числа (від 1 і більше) визначають порядок вибору квадратів (і відповідно точок всередині них) на кожному етапі; раніше оброблені квадрати затемнені.

Для довільних наборів точок такий алгоритм (як і всі інші ітеративні алгоритми) має трудомісткість О(N²). Якщо вихідні точки мають рівномірний розподіл, то трудомісткість алгоритму в середньому випадку буде О(N). Крім того, в [10] показується, що якщо вихідні точки задовольняють деяким фіксованим (не імовірнісним) обмеженням, то трудомісткість алгоритму буде і в гіршому випадку О(N)

Недоліком попередніх двох алгоритмів (смугового і квадратного) є те, що при вставці кожної нової точки відбувається часта побудова довгих вузьких трикутників, які в подальшому перебудовуються. В алгоритмі з згущенням точок, як правило, вдається позбутися таких ситуацій, рівномірно послідовно вставляючи в тріангуляцію вузли. За рахунок цього даний алгоритм будує менше вузьких трикутників і тому швидше виконується на реальних даних, ніж багато інших алгоритми.

2.4.4. Ітеративні алгоритми з сортуванням уздовж кривої, яка наповнює площину. Ідея цих алгоритмів полягає в "розгортанні" площини в одну пряму, при цьому близькі точки на цій прямій будуть також близькі і на вихідній площині. У теорії фракталів відомо значна кількість кривих, що заповнюють площину. Одними із найбільш відомих і зручних для застосування в задачі побудови тріангуляції є криві Пеано і Гільберта [5].

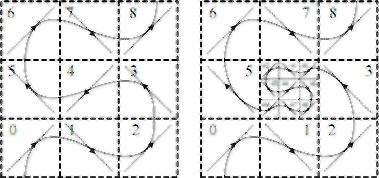
(а) (б)

Рис. 19. Побудова кривої Пеано (а-перша ітерація, б - друга ітерація в центральному квадраті)

При побудові кривої Пеано використовується представлення точок в системі числення за основою 9. На першому кроці область визначення вихідних точок тріангуляції ділиться на дев'ять рівних квадратів. Ці квадрати нумеруються від 0 до 8; утворюється крива першій ітерації (рис. 19а). Далі кожен з квадратів ділиться ще на дев'ять частин; до номера, отриманого на першій ітерації, в кінці додається нова цифра (рис. 19б).

При побудові тріангуляції необхідно для кожної вихідної точки обчислити код Пеано, відсортувати точки за цим кодом і в цьому порядку вносити їх в тріангуляцію.

Аналогічно кривої Пеано можна використовувати криву Гільберта. При цьому розподіл області розміщення вихідних точок виконується на чотири частини відповідно до рис. 20.

Рис. 20. Побудова кривої Гільберта

Трудомісткість ітеративних алгоритмів з сортуванням вздовж кривих Пеано і Гільберта складає в гіршому випадку О(N²), а в середньому - О(N). На практиці дані алгоритми працюють приблизно з тією ж швидкістю, що і ітеративний смуговий алгоритм.

2.4.5. Ітеративний алгоритм з сортуванням по Z-коду. У ітеративному алгоритмі з сортуванням по Z-коду для кожної точки площині (х ,у) будується спеціальний Z-код. Потім виконується сортування всіх точок за цим кодом, після чого точки вставляються в тріангуляцію в цьому порядку.

Для побудови Z-коду потрібно розбити прямокутну область розміщення вихідних точок на чотири рівних прямокутника і занумерувати їх двійковими числами від 0 до 11₂ відповідно до (рис. 21а). Далі кожен з отриманих прямокутників треба знову розбити на чотири частини, знову занумерувати їх двійковими числами від 0 до 11₂ і додати до кінця коду, отриманого раніше (рис. 21б). При необхідності так можна рекурсивно продовжувати досить далеко.

(а) (б) (в)

Рис. 21. Ітеративний алгоритм з сортуванням по Z-коду (а, б - порядок вставки точок в тріангуляцію, в - побітове отримання Z-коду)

Однак на практиці такі складні маніпуляції проробляти не потрібно. Насправді Z-код можна дуже просто отримати. Для цього потрібно спочатку перейти від вихідних координат (х, у) до цілочисельних координат (Х, Y), що змінюються в діапазоні (0, 2^k – 1), де k - деяке ціле число. Після цього потрібно взяти по черзі всі біти координат X і Y з першого по останній і сформувати нову бітову послідовність (рис. 21 в).

На відміну від кодів Пеано і Гільберта в Z-коді близькі значення коду не завжди відповідають близькому розташуванню на площині, тому пошук трикутників іноді виконується довше, ніж у попередньому алгоритмі. Але при цьому сама процедура обчислення коду працює значно швидше.

Трудомісткість даного алгоритму становить в гіршому випадку О(N²), а в середньому – О(N). На практиці даний алгоритм показує практично ту ж саму швидкість роботи, що й алгоритми з сортуванням вздовж кривої, що заповнює площину.

3. Алгоритми злиття. Концептуально всі алгоритми злиття припускають розбиття вихідної множини точок на кілька підмножин, побудова тріангуляції на цих підмножинах, а потім об'єднання (злиття) декількох тріангуляції в одне ціле.

3.4. Алгоритм злиття «Розділяй і володарюй». У цьому алгоритмі [12, 18] множина точок розбивається на дві якомога рівні частини, причому на різних рівнях рекурсії зазвичай приміняється розбиття горизонтальними і вертикальними лініями по черзі (рис. 22). Алгоритм тріангуляції рекурсивно застосовується до підчастин, а потім здійснюється злиття (об'єднання) отриманих підтріангуляцій. Рекурсія припиняється при розбитті всієї множини на досить маленькі частини, які можна легко протріангулювати яким-небудь іншим простим способом. На практиці зручно розбивати всі множини на частини по три і по чотири точки.

Рис. 22. Розбиття множини точок в алгоритмі тріангуляції «Розділяй і володарюй»

Якщо припустити, що число точок в тріангуляції завжди більше п'яти, то всю множину точок можна розбити на елементарні частини по три і по чотири точки. Дійсно, N > 5:

Рекурсивний алгоритм тріангуляції «Розділяй і володарюй» можна умовно записати наступним чином.

Крок 1. Якщо число точок N = 3, то побудувати тріангуляцію із одного трикутника.

Крок 2. Інакше, якщо кількість точок N = 4, то побудувати тріангуляцію з двох або трьох трикутників.

Крок 3. Інакше, якщо кількість точок N = 8, то розбити множини точок на дві частини по чотири точки, рекурсивно застосувати алгоритм, а потім склеїти тріангуляції.

Крок 4. Інакше, якщо кількість точок N <12, то розбити множину точок на дві частини по 3 і N-3 точки, рекурсивно застосувати алгоритм, а потім склеїти тріангуляції.

Крок 5. Інакше (кількість точок N ≥ 12) розбити множину точок на дві частини по [N/2] і [N/2] точки, рекурсивно застосувати алгоритм, а потім склеїти тріангуляції.

Елементарні множини ID трьох або з чотирьох елементів (рис. 23) легко тріангулюются (можна навіть просто перебрати множину всіх можливих варіантів).

Рис. 23. Тріангуляції множин з трьох і чотирьох точок

Трудомісткість алгоритму «Розділяй і володарюй» складає О(N log N) в середньому і найгіршому випадках. Основна і найскладніша частина цього алгоритму полягає в злитті двох часткових тріангуляцій. Для цього може використовуватися кілька еквівалентних процедур злиття (звернімо увагу, що всі створені часткові тріангуляції є опуклими і нижченаведені процедури істотно використовують цей факт):

1. «Видаляй-і-будуй».

2. «Будуй-і-перебудовувай».

3. «Будуй, перебудовуючи».

3.1.1.Злиття тріангуляції «Видаляй-і будуй». Дана процедура злиття тріангуляції була запропонована в [12, 18] як частина відповідного алгоритму тріангуляції «Розділяй і володарюй».

Рис. 24. Злиття тріангуляції (а - пошук дотичних, б - пошук найближчого сусіда Делоне для базової лінії, в - побудова трикутника)

Спочатку для двох тріангуляцій знаходяться дві загальні дотичні Р₀Р₁ і Р₂Р₃ перша з яких стає поточної базової лінією (рис. 24 а). Потім від базової лінії починається заповнення трикутниками проміжку між тріангуляціями. Для цього необхідно знайти найближчий до базової лінії вузол будь-який з двох часткових тріангуляцій - так званого сусіда Делоне для базової лінії. Пошук цього сусіда можна уявити собі як зростання "бульбашки" від базової лінії, поки не зустрінеться якийсь вузол. «Бульбашка» - це коло, що проходить через точки P₀ і P₁, з центром на серединному перпендикулярі до базової лінії. Наприклад, на рис. 24 б першим таким знайденим вузлом стає точка А. На знайденому вузлі і базової лінії будується новий трикутник (у нашому випадку ΔP₀P₁A).

Однак при цьому іноді виникає необхідність заздалегідь видалити деякі раніше побудовані трикутники, які перекриваються новим трикутником. Так, на рис. 24б повинен бути видалений ΔP₀BA. Після цього відкрита сторона нового трикутника стає новою базовою лінією (на рис. 24 в – AP₁), і цикл триває, поки не буде досягнута друга дотична.

Дана процедура злиття дуже схожа на алгоритми прямої побудови тріангуляції, які обговорювались нижче. Тому їй властиві ті ж самі недоліки, а саме відносно великі витрати часу на пошук чергового сусіда Делоне. В цілому ця процедура має трудомісткість О(N) відносно загальної кількості точок у двох об'єднаних тріангуляціях [18].

3.1.2. Злиття тріангуляції «Будуй-і-перебудовуй». У процедурі злиття тріангуляції «Будуй-і-перебудовуй» є два етапи [8]. Спочатку будуються заповнюючі зону злиття трикутники між дотичними (рис. 25а). Для цього перша дотична P₀P_i робиться поточною базової лінії Q₁Q₂. Щодо поточної базової лінії розглядаються дві наступні точки N₁ і N₂ уздовж кордонів зливающихся тріангуляцій. З двох трикутників ΔQ₁Q₂N₁ і ΔQ₁Q₂N₂ вибирається той, який, по-перше, можна побудувати (тобто Q₂Q₁N₁ ˂ 180° для першого і Q₁Q₂N₂<180 ° для другого трикутника), і, по-друге, максимум мінімального кута якого більше (так вибирається «більш рівносторонній» трикутник, який з меншою ймовірністю буде перебудований в майбутньому). Після цього відкрита сторона новозбудованого трикутника стає новою базовою лінією (рис. 25б). Далі цикл побудови трикутників триває, поки не буде досягнута друга дотична .

Рис. 25. Злиття тріангуляції (а - попереднє злиття, б - вибір чергового трикутника, в - фінальна тріангуляція після перебудовування трикутників)

На другому етапі всі новозбудовані трикутники перевіряються на виконання умови Делоне з іншими трикутниками і при необхідності виконується перебудува трикутників (рис. 25 в).

Процедура злиття «Будуй-і-перебудовуй» значно простіша в реалізації попередньої і зазвичай працює помітно швидше на реальних даних. В цілому вона має в гіршому випадку трудомісткість О(N) відносно загальної кількості точок у двох тріангуляцій, які зливаються, а в середньому на більшості поширених розподілів О(√N) або О(М), де М – загальна кількість точок вздовж кордонів тріангуляцій, які зливаються [8].

3.1.3. Злиття тріангуляції «Будуй, перебудовуючи». Процедура, що реалізує це злиття, відрізняється від попередньої лише тим, що перебудування виконуються не на другому етапі роботи, а безпосередньо після побудови чергового трикутника (рис. 26) [8]. У такому разі відпадає необхідність пам'ятати список всіх побудованих трикутників, дещо зменшується загальна кількість перевірок умови Делоне і кількість виконаних перебудувань. Однак при цьому для деяких структур даних (наприклад, «Вузли і трикутник») необхідно докладати додаткові зусилля для збереження посилання на поточну базову лінію, тому що утворює її трикутник може бути перебудований.

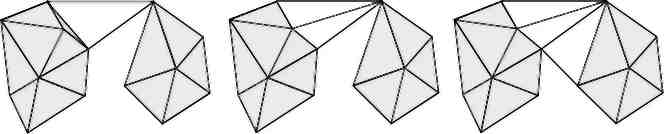
(а) (б) (в)

Рис. 26. Кроки злиття «Будуй, перебудовуючи" (а - побудова першого трикутника, б - негайні перестроювання, в - побудова другого трикутника)

В цілому ця процедура має таку ж трудомісткість, що і попередня, і на практиці працює трохи повільніше неї.

3.2. Рекурсивний алгоритм з розрізанням по діаметру. Даний алгоритм тріангуляції схожий на «Розділяй і володарюй», але відрізняється від нього способом поділу множини вихідних точок на дві частини і процедурою злиття двох часткових тріангуляції. Використана тут процедура злиття описана в [23].

Для поділу множини точок на дві частини спочатку будується опукла оболонка всіх вихідних точок (ця операція виконується за час О(N) [7]). Далі по опуклій оболонці обчислюється діаметр D₁D₂ (рис. 27а) [7]. Трудомісткість цієї операції складає в гіршому випадку О(NlogN), а в середньому - О(N). Потім необхідно знайти таку пару точок P₁ і Р₂, щоб відрізок Р₁Р₂ був "майже" перпендикулярний діаметру D₁D₂ і ділив множину всіх вихідних точок приблизно на дві рівні частини. В якості першого наближення для P₁ і Р₂ можна взяти точки посередині вздовж опуклої оболонки між D₁ і D₂ (рис. 27 а).

(а) (б) (в) (г)

Рис. 27. Злиття тріангуляції (а - пошук діаметра і точок поділу, б - роздільна тріангуляція, в - з'єднання тріангуляції по загальному ребру, г - перебудування)

Після вибору P₁ і Р₂ вся множина вихідних точок ділиться на дві частини, причому P₁ і Р₂ потрапляють в обидві множини. Після цього даний алгоритм тріангуляції застосовується рекурсивно до обох частин (рис. 27б). Потім обидві отримані тріангуляції з'єднуються вздовж загального ребра P₁P₂ (рис. 27в) і виконуються необхідні перебудови пар сусідніх трикутників для виконання умови Делоне (рис. 27г).

Даний алгоритм злиття в порівнянні з «Розділяй і володарюй» складніший у процедурі поділу точок на частини, але простіший у злитті. Трудомісткість алгоритму з розрізанням по діаметру складає в гіршому і в середньому випадках О(N logN). В цілому алгоритм працює трохи повільніше, ніж «Розділяй і володарюй».

3.3. Смугові алгоритми злиття. Логарифмічна складова в трудомісткості двох попередніх алгоритмів породжена їх рекурсивним характером. Позбувшись рекурсії, можна зробити спробу поліпшити і трудомісткість тріангуляції. В [8] пропонується розбити вихідну множину точок на такі підмножини, щоб побудова по них тріангуляцій займало мінімальний час (наприклад, за рахунок застосування спеціальних алгоритмів, оптимізованих для конкретних конфігурацій точок).

Основна ідея смугових алгоритмів злиття передбачає розбиття всього вихідного безлічі точок на деякі смуги і застосування швидкого алгоритму отримання неопуклих тріангуляцій смуги точок. Після отримання множини часткових смугових тріангуляцій вони об'єднуються, при цьому, так як смуги неопуклі, доводиться 1) або добудовувати смуги до опуклих і потім використовувати звичайний алгоритм злиття з алгоритму «Розділяй і володарюй», 2) або застосовувати більш складний, але більш ефективний алгоритм, що дозволяє з'єднувати неопуклі тріангуляції.

У цілому алгоритми смугового злиття логічно складаються з трьох послідовних кроків.

Крок 1. Розбиття всієї вихідної множини точок на деякі смуги.

Крок 2. Застосування спеціального швидкого алгоритму отримання неопуклих тріангуляцій смуги точок.

Крок 3. Злиття отриманих підтрінангуляцій.

Розглянемо ці кроки докладніше.

Крок 1. Множина усіх точок розбивається по деякій кількості стовпців за принципом однакової ширини колонок або однакової кількості точок у стовпцях (за допомогою цифрового сортування). Кількість точок у кожному стовпці має вийти не менше трьох (цього вимагає алгоритм, застосований на наступному кроці алгоритму). Якщо це не виконується для будь-якого стовпця, то його потрібно приєднати до сусіднього. Трудомісткість даного кроку становить O(N) відповідно до трудомісткості застосовуваних алгоритмів розбиття.

Крок 2. Всі крапки всередині стовпців сортуються по вертикалі (по координаті Y), і потім кожен стовпець тріангулюється окремо. Для цього використовується спеціальний алгоритм тріангуляції (рис. 28а). Спочатку на трьох самих верхніх точках в стовпці будується перший трикутник і позначається як поточний. Потім послідовно перебираються всі інші точки в стовпці (починаючи з четвертої) зверху вниз і додаються до часткової тріангуляції. Нехай ΔАВС є поточним, точка В має найменшу з точок трикутника координату, а Х - чергова додана точка зі стовпця. На черговому кроці необхідно зробити вибір чергового створюваного ΔАВХ або ΔВСХ (рис. 28 б). Іноді один з цих трикутників побудувати неможливо через одержуваних тоді перетинів різних відрізків тріангуляції, і питання вибору тоді не варто. Якщо ж побудувати можна два трикутника, природно вибрати той, у якого мінімальний з кутів більше, тому що тоді з більшою ймовірністю в майбутньому не доведеться його перебудовувати через невиконання умови Делоне.

(а) (б)

Рис. 28. Тріангуляція смуги точок

Після побудови чергового трикутника треба перевірити умову Делоне для знову створених пар сусідніх трикутників і при необхідності перебудувати їх. Зауважимо, що при такому алгоритмі буде побудована неопукла тріангуляція смуги точок.

Одним з найважливіших параметрів алгоритму тріангуляціі стовпця точок є вибір кількості смуг, який здійснюється виходячи з мінімізації числа наступних перебудувань пар сусідніх трикутників. Якщо припустити, що всі N вихідних точок розподілені в прямокутній області шириною а і висотою b, то число смуг обчислюється як т = √sNa/b, де s - коефіцієнт розбиття [8].

На практиці значення s слід взяти ≈ 0,11 - 0,15.

Трудомісткість даного кроку буде в середньому O(N) за умови вибору оптимальної кількості смуг.

3.3.1. Алгоритм опуклого смугового злиття. Покрокова схема роботи алгоритму опуклого смугового злиття схематично зображено на рис. 29 а-г. Основна його ідея полягає в побудові опуклих смугових тріангуляції і подальшого застосування будь-якого алгоритму злиття, використаного в алгоритмі «Розділяй і володарюй».

Рис. 29. Алгоритм опуклого смугового злиття (а-г - кроки роботи алгоритму, д – добудова опуклості)

Крок 3а. Виконується обхід всіх граничних вузлів P_і часткових тріангуляцій. Аналізуються сусідні до P_i вздовж границі вузли P_і+1 і Р_і-1 . Якщо Z.P_і-1P_іP_і+1<180°, то в точці Р_і - порушується умова опуклості тріангуляції і необхідно побудувати ΔР_і-1Р_іР_і+1, а подальший аналіз граничних вузлів треба продовжити з попереднього вузла P_i (рис. 29 д).

Крок 3б. Далі необхідно послідовно склеїти всі стовпці один з одним, використовуючи алгоритм злиття з алгоритму тріангуляції «Розділяй і володарюй».

В цілому трудомісткість алгоритму опуклого смугового злиття складає в середньому O(N). Однак даний алгоритм робить багато зайвої роботи, так як при побудові опуклої оболонки вузької смуги зазвичай виходять довгі вузькі трикутники, які майже завжди доводиться перебудовувати при злитті. Цей недолік виправляється в наступному алгоритмі неопуклого злиття.

3.3.2. Алгоритм неопуклого смугового злиття. Покрокова схема роботи алгоритму неопуклого смугового злиття схематично зображено на рис. 30а-в.

(а) (б) (в) (г) (д)

Рис. 30. Алгоритм неопуклого смугового злиття (а-в - кроки роботи алгоритму, г - злиття смуг, д - локальне добудовування опуклості)

Крок 3. На вхід алгоритму неопуклого злиття подаються неопуклі смугові тріангуляції. В ході роботи алгоритму перед черговою побудовою з'єднуючого ребра і, відповідно, трикутника проводиться добудова опуклості на деякій відстані від з'єднуючого ребра. Розглянемо це докладніше. Нехай на черговому кроці злиття побудований відрізок Р₁Р₂ (Р₁ - на лівій тріангуляції, Р₂ - на правій). Нехай N₁,N₂ - сусідні точки по границі тріангуляції (наступні нижче Р₁,Р₂). У попередньому алгоритмі на черговому кроці потрібно було вибрати, який трикутник будувати ΔP₁ P₂ N₁ або ΔP₁ P₂ N₂ (Рис - 30г). В алгоритмі опуклого злиття істотно використовується та властивість, що межа першої тріангуляції вище N₂ (починаючи з P₁ і нижче) і границя другої тріангуляції вище N₁ (починаючи з Р₂ і нижче) опуклі. В алгоритмі неопуклого злиття необхідно проаналізувати опуклість границі і визначити першу точку D₁ (D₂), починаючи з P₁ (P₂), де порушується опуклість, і запам'ятати наступну за нею точку С₁ ( С₂). Тоді перед аналізом, який трикутник злиття будувати, проводиться наступна перевірка. Якщо С₁ ( С₂) вище N₂ (N₁), то добудовується опукла оболонка на границі від С₁ до Р₁ (від С₂ до Р₂) і шукаються наступні точки D і С, якщо вони існують (рис. 30д).

При такому підході вдасться помітно зменшити число перебудов, а отже, і час роботи алгоритму. В [8] показано, що алгоритм неопуклого злиття працює приблизно на 10 - 15% швидше, ніж алгоритм опуклого злиття.

4. Алгоритми прямої побудови. У всіх розглянутих алгоритмах на різних етапах по ¬ будови тріангуляції можуть бути побудовані трикутники, які надалі будуть перебудовані у зв'язку з невиконанням умови Делоне.

Основна ідея алгоритмів прямої побудови полягає в тому, щоб будувати тільки такі трикутники, які задовольняють умові Делоне в кінцевій тріангуляції, а тому не повинні перебудовуватися [23].

4.1. Покроковий алгоритм. Покроковий алгоритм [23], відомий також як алгоритм прямого перебору і метод активних ребер, концептуально схожий на алгоритм злиття тріангуляції «Видаляй-і-будуй», описаний вище.

В алгоритмі спочатку вибирається деяка базова лінія АВ, починаючи від якої будуть будуватися всі наступні трикутники (рис. 31). Базова лінія береться як один з відрізків багатокутника опуклої оболонки всіх вихідних точок тріангуляції.

Рис. 31. Вибір чергової точки для включення в тріангуляцію.

Далі для базової лінії необхідно знайти найближчого сусіда Делоне. Процес пошуку можна представити собі як зростання "'бульбашки" від базової лінії, поки не зустрінеться якийсь вузол. "Бульбашка" - це коло, що проходить через точки А і В, з центром на серединному перпендикулярі до базової лінії.

На покроковому алгоритмі для пошуку сусіда Делоне потрібно вибрати серед усіх точок Р_і тріангуляції таку, що AP_іB буде максимальним (наприклад, на рис. 31 буде обрана точка Р₂). Знайдений сусід Делоне з'єднується відрізками з кінцями базової лінії і утворює ΔАР_іВ. Нові ребра АР_і і ВP_i побудованого трикутника позначаються як нові базові лінії і процес пошуку трикутників триває.

Трудомісткість покрокового алгоритму становить О(N²) в середньому і найгіршому випадках. Через настільки велику трудомісткість на практиці такий алгоритм практично не застосовується.

4.2. Покрокові алгоритми з прискоренням пошуку сусідів Делоне. Квадратична складність покрокового алгоритму обумовлена трудомісткою процедурою пошуку сусіда Делоне. У наступних двох алгоритмах пропонуються два варіанти його прискорення.

4.2.1. Покроковий алгоритм з бінарним деревом пошуку. У покроковому алгоритмі з бінарним деревом пошуку спочатку всі вихідні точки тріангуляції поміщаються в будь бінарне дерево (наприклад, k-D-дерево), що дозволяє виконувати регіональний пошук в заданому квадраті зі сторонами, паралельними осям координат.

Рис. 32 Вибір чергової точки в клітинному алгоритмі

Далі при виконанні пошуку чергового сусіда Делоне імітується поступове зростання "бульбашки". Початкова «бульбашка» визначається як коло, діаметром якої є поточна базова лінія.

Надалі, якщо всередині поточної «бульбашки» не знайдено ніяких точок, то розмір «бульбашки» збільшиться, наприклад, у два рази (на рис. 32 цифрами позначені можливі етапи росту «бульбашки»). Для визначення точок, які потрапили в поточну бульбашку, виконується запит до бінарного дерева на пошук усіх точок всередині мінімального квадрата, який охоплює поточну «бульбашку». Серед знайдених в квадраті точок відкидаються всі, які не потрапили в поточну «бульбашку». Далі серед решти точок прямим перебором знаходиться шуканий сусід Делоне.

Трудомісткість даного алгоритму з k-D-деревом в середньому на ряду поширених розподілів становить О(N log N), а в гіршому випадку - О(N²).

4.2.2. Клітинний покроковий алгоритм. У клітинному покроковому алгоритмі пропонується побудувати клітинне розбиття площини, а пошук чергового сусіда Делоне вести, послідовно перебираючи точки в прилеглих до базової лінії клітинах [2]. Для цього на першому етапі вся множина вихідних точок розбивається вертикальними і горизонтальними лініями рівновіддаленими на клітини і всі точки поміщаються в списки, які відповідають цим клітинам. Загальна кількість клітин має бути θ(N).

Далі при виконанні пошуку чергового сусіда Делоне імітується зростання "бульбашки" і перевіряються всі клітини з точками в порядку близькості клітин до базової лінії (на рис. 33 цифрами позначено порядок обходу клітин). Трудомісткість даного алгоритму в середньому на ряді поширених розподілів становить О(N) [2], а в гіршому випадку - O(N²).

Рис. 33. Вибір черговий точки в клітинному алгоритмі

5. Двопрохідний алгоритми. При побудові тріангуляції Делоне ітеративними алгоритмами і алгоритмами злиття для кожного споруджуваного трикутника після побудови повинна бути перевірена умова Делоне. При цьому доводиться проводити перевірки для трьох пар, що відповідають трьом сусіднім трикутникам до цього. Якщо перевірка не витримана, повинні послідувати побудова трикутників і нова серія перевірок. На практиці досить велику частку часу забирають якраз перевірки на умову Делоне і перебудування.

Для спрощення логіки роботи алгоритмів можна за перший прохід побудувати деяку тріангуляцію, ігноруючи виконання умови Делоне, а після цього за другий прохід перевірити те, що отримали і провести потрібні поліпшуючі перебудування для приведення тріангуляції до тріангуляції Делоне. Допустимість такої двопрохідної стратегії встановлюється в теоремі 1.

5.1. Двопрохідний алгоритми злиття. Найбільш вдало двопрохідна стратегія застосовується до алгоритмів злиття. У них доводиться прикладати чимало алгоритмічних зусиль для того, щоб забезпечити роботу з «поточним трикутником» (наприклад, при обході тріангуляції по границі, при злитті, побудові опуклої оболонки), тому що після того, як трикутник побудований, він може тут же в результаті невдалої перевірки на умову Делоне зникнути, а на його місці можуть з'явитися інші трикутники. Крім того, в алгоритмах злиття відразу будується досить багато трикутників, які в подальшому не перебудовуються. Загальна кількість виконуваних перебудов в алгоритмі неопуклого злиття становить близько 35% від загального числа трикутників в кінцевій тріангуляції, в алгоритмі опуклого злиття - 70%, в алгоритмі «Розділяй і володарюй» - 90% i, в той же час в простому ітеративному алгоритмі-140% . Саме тому найбільш добре для двопроходної стратегії підходить алгоритм неопуклого злиття. В алгоритмах «Розділяй і володарюй» опуклого злиття і рекурсивному з розрізанням по діаметру на проміжних етапах будується деяка кількість довгих вузьких трикутників, які зазвичай потім перебудовуються.

На рис. 34 наведено приклад застосування двопроходної стратегії до алгоритму опуклого смугового злиття. В [8] показується, що двоетапні смугові алгоритми і «Розділяй і володарюй» працюють у середньому на 10 - 20% швидше оригінальних алгоритмів. Це зокрема пояснюється деяким спрощенням логіки роботи алгоритмів.

5.2. Модифікований ієрархічний алгоритм. Для ітеративних алгоритмів двопрохідна с стратегія, як правило, не годиться, тому що відразу ж утворюються вузькі довгі трикутники, які в подальшому діляться на інші ще менші і ще більш вузькі.

(а) (б) (в) (г) (д)

Рис. 34. Двопрохідний алгоритм опуклого смугового злиття (а-г - побудова деякої тріангуляції, д - повне перебудовування)

Проте, в [24] описується модифікований ієрархічний алгоритм, що є, по суті, є звичайним ітеративним алгоритмом, що виконується за два проходи.

Як і для оригінального простого ітеративного алгоритму, трудомісткість даного становить в гіршому випадку O(N²), а в середньому - O(N^3/2). На практиці цей алгоритм працює значно повільніше початкового. Тим не менш, він використовується для побудови спеціальних ієрархічних тріангуляції, що застосовуються для роботи з великими наборами вихідних даних.

5.3. Лінійний алгоритм. Лінійний алгоритм (алгоритм лінійного замітання площини) можна представити як окремий випадок двопрохідного алгоритму опуклого злиття з однією смугою. В даному алгоритмі спочатку всі вихідні точки площини сортуються по вертикалі (рис. 35а). Потім, послідовно перебираючи точки зверху вниз, з'єднуються в одну неопуклу тріангуляцію (рис. 35б). Далі тріангуляція добудовується до опуклої (мал. 35 в). І на закінчення виконується повна перебудова тріангуляції для виконання умови Делоне (рис. 35 г).

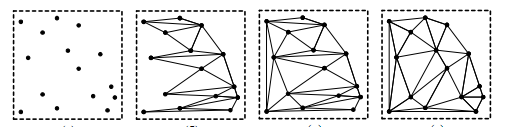
(а) (б) (в) (г)

Рис. 35. Лінійний алгоритм (а - вихідні точки, б - неопукла тріангуляція, в – добудова до опуклої, г - перебудова тріангуляції)

Трудомісткість такого алгоритму становить в середньому О(N). Проте, на практиці цей алгоритм працює істотно повільніше повноцінного алгоритму смугового злиття.

5.4. Віяловий алгоритм. У віяловому алгоритмі тріангуляції (алгоритмі радіального замітання площини) спочатку з вихідних точок вибирається та, яка знаходиться якомога ближче до центру мас усіх точок. Далі інших точок обчислюється полярний кут відносно вибраної центральної точки і всі точки сортуються по цьому куті (рис. 36б). Потім всі точки з'єднуються ребрами з центральною точкою і сусідніми в відсортованому списку (рис. 36в). Потім тріангуляція добудовується до опуклої (рис. 36 г). І на закінчення виконується повна перебудова тріангуляції для виконання умови Делоне (рис. 36 д).

Трудомісткість такого алгоритму складає в середньому О(N). Алгоритм працює приблизно з тією ж швидкістю, що і попередній лінійний алгоритм.

5.5. Алгоритм рекурсивного розщеплення. Алгоритм рекурсивного розщеплення працює в два проходи [19]. Другий прохід аналогічний всім двопрохідним алгоритмам тріангуляції, а перший схожий на рекурсивний алгоритм з розрізанням по діаметру, але розрізання відбувається не одним відрізком, а деякою ламаною.

Перед початком роботи алгоритму обчислюється опукла оболонка всіх вихідних точок. На кожному кроці рекурсії для заданої множини точок та їх оболонки (не обов'язково опуклої) виконується поділ всіх точок на дві частини. Для цього на оболонці знаходяться протилежні точки Р₁ і Р₂ , які ділять багатокутник оболонки приблизно навпіл (рис. 37а).

Рис. 36. Лінійний алгоритм (а - вихідні точки, б - кругове сортування, в - неопукла тріангуляція, г - добудова до опуклою, д - перебудова тріангуляції)

Рис. 37. Алгоритм рекурсивного розщеплення (а - вибір напрямку та коридору, б-г – кроки розщеплення, д - перебудова тріангуляції)

(а) (б) (в) (г) (д) Рис. 38. Смуговий алгоритм (а - розбиття на смуги, б - побудова в смугах ламаних, в - злиття смуг, г - добудова до опуклості, д - перебудова тріангуляції)

Потім знаходяться всі точки Si серед заданих, не потрапляють на оболонку і знаходяться від прямої P₁P₂ не більше ніж на заданій відстані λ, тобто потрапляють в деякий коридор розщеплення (рис. 37а). Потім точки P₁, S_i і Р₂ послідовно з'єднуються в ламану, яка розбиває вихідну множину точок на дві частини. Розділяюча ламана при цьому потрапляє в обидві множини (рис. 37б). Крім того, оскільки оболонка неопукла, то необхідно виключити випадки можливого перетину побудованої ламаної з оболонкою. Якщо отримані множини не є трикутниками, то до них знову рекурсивно застосовується даний алгоритм (рис. 37 в). Після побудови тріангуляції окремих частин виконується їх з'єднання вздовж розділеної ломаної.

Теоретично даний алгоритм рекурсивного розщеплення має трудомісткість О(N log N) в середньому і гіршому випадках [19]. Однак на практиці процедура розщеплення є складною для реалізації, повільною в роботі і в цілому алгоритм працює істотно повільніше будь-яких двопрохідний алгоритмів злиття.

5.6. Стрічковий алгоритм. Ідея стрічкового алгоритму запропонована Ю.Л. Костюком. Деякі елементи цього алгоритму схожі на алгоритм неопуклого злиття.

На першому кроці всі точки розбиваються на смуги (рис. 38 а). Потім точки сортуються всередині смуг і послідовно з'єднуються в ламані (рис. 38 6). Потім всі смуги склеюються між собою, використовуючи процедуру злиття з алгоритму неопуклого смугового злиття (рис. 38 в). Після цього отримана тріангуляція добудовується до опуклої (рис. 38г) і проводиться повна перебудова тріангуляції для виконання умови Делоне (мал. 38 д).

В даному алгоритмі використовується процедура злиття, що з'єднує ламані-ребра майбутньої тріангуляції. Тому найбільш зручно цей алгоритм реалізується на структурі даних «Вузли, ребра і трикутники», що представляє ребра в явному вигляді.

Трудомісткість даного алгоритму становить в середньому O(N).

Висновок. Підводячи підсумки даного огляду алгоритмів побудови тріангуляції Делоне, приведемо порівняльну таблицю розглянутих алгоритмів. У ній для кожного алгоритму наводяться трудомісткості в гіршому і середньому випадках, тривалість роботи на 10 000 точок у відносних одиницях та авторська експертна оцінка простоти реалізації за п'ятибальною системою (чим більше зірочок, тим алгоритм краще). Всі наведені оцінки часу отримані автором при реалізації алгоритмів в одному стилі (на структурі даних «Вузли й трикутники»), в одному програмному середовищі (Borland Pascal) і на одній апаратній платформі (Intel). Деякі з алгоритмів автором не реалізовані, тому в таблиці там стоять прочерки. Зауважимо, що оцінки часу достатньо умовні; мабуть, вони будуть істотно відрізнятися в різних реалізаціях. Більш детальні результати порівнянь окремих алгоритмів наведено в [8].

Загалом з усієї безлічі представлених алгоритмів з досвіду автора найкраще себе зарекомендували алгоритм динамічного кешування. Приблизно так само добре працює алгоритм пошарового згущення. Що важливо, обидва ці алгоритму легко програмуються на будь-яких структурах даних. З інших хороших алгоритмів слід зазначити двопрохідний алгоритм неопуклого смогового злиття і стрічковий алгоритм, але вони дещо складніші в реалізації.