Введение в многомерный статистический анализ / page14-58 / ander2_2_1

(45)

(46)

положителен. Поэтому (для невырожденных распределений, см. § 2.4).

В качестве особого случая изложенной теории мы рас­смотрим двумерное нормальное распределение. Среднее зна­чение вектора равно

(47)

ковариационная матрица может быть записана следующим образом:

(48)

где является дисперсией Х₁ ,— дисперсией Х₂ и — коэффициентом корреляции между Х₁ и Х₂ . Легко про­верить, что обращение (48) есть

(49)

Плотность вероятности Х₁ и Х₂ равна

. (50)

Ниже будет показано, что если = 0, то Х₁ и Х₂ незави­симы; если > 0, то между Х₁ и Х₂ существует положи­тельная связь; и если < 0, то между Х₁ и Х₂ — отрица­тельная связь.

Отметим, что плотность вероятности (43) в р-мерном евклидовом пространстве постоянна на эллипсоидах

(51)

для каждого положительного значения с. Центром каждого эллипсоида является точка. Форма и положение эллип­соида определяются значением, а размеры (при фикси­рованном )— значением с.

Рассмотрим подробно двумерный случай плотности вероят­ности (50). Преобразуем координаты посредством равенства (i = 1, 2) так, чтобы центры линий, на кото­рых плотность распределения постоянна, находились в начале координат. Эти линии определяются уравнениями

(52)

Отрезки, отсекаемые на осях у₁ и у₂, равны между собой. Если > 0, то большая ось эллипса наклонена под углом 45° к оси х и ее длина равна, а длина малой оси равна . Если < 0, то большая ось эллипса наклонена под углом 135° к оси х и ее длина равна , а длина малой оси равна .В рас­сматриваемом случае мы можем считать, что плотность рас­пределения графически изображается поверхностью над пло­скостью. Контуры равных плотностей аналогичны контурам равных высот на топографической карте; они показывают форму «холма» (или вероятностной поверхности). Если > О, то эта поверхность простирается вдоль линии с положитель­ным наклоном; большая часть «холма» в этом случае нахо­дится в первом и третьем квадратах. При обратном переходе к координатам мы растягиваем каждый контур, в раз в направлении i-й оси и переносим центр в точку

Численные значения функции распределения одномерной нормальной случайной величины могут быть получены из таблиц, приводимых в большинстве учебников по статистике. Численные значения для

(53)

где и можно найти у Пирсона [2], [3]. Пирсон также показал, что

(54)

где так называемые четырехклеточные (тетрахорические) функции табулированы у Пирсона [2], [3] до Кэндалл [2] показал, что выражение (54) может быть рас­пространено на F(x₁ ,..., х_n).

2.4. Распределение линейной комбинации нормально

распределенных величин; независимость величин;

частные распределения

Одной из причин изучения многомерных нормальных рас­пределений является то, что частные и условные распреде­ления, полученные из многомерных нормальных распределе­ний также нормальны. Более того, линейные комбинации нормально распределенных величин также распределены нор­мально. Сперва мы покажем, что в результате невырожден­ного линейного преобразования вектора, совместное распре­деление компонент которого нормально, мы получаем вектор, совместное распределение компонент которого также нор­мально.

Теорема 2.4.1. Пусть р-мерный вектор X распре­делен .

Тогда

Y = CX . (1)

распределен для невырожденных С.

Доказательство. Плотность распределения Y полу­чается из плотности распределения X путем за­мены х на у такое, что

(2)

и умножением на определитель преобразования (2), который равен Этот определитель можно представить в виде

(3)

Квадратичная форма в показателе плотности есть

(4) Преобразование (2) переводит Q в

(5)

так как согласно свойству транспонирован­ных матриц, и СС ^-1 = I . Таким образом, плотность распре­деления вероятностей Y будет

Теорема доказана.

Пусть теперь рассматриваются два множества случайных величин

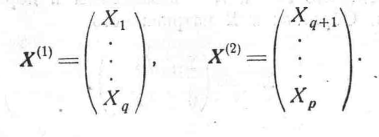
Х₁, ..., X_q и Х_q+1, ..., X_р, заданные в виде век­торов

(7)

Эти случайные величины образуют случайный вектор

(8)

Предположим теперь, что р величин имеют совместное нормальное распределение со средними значениями

(9) и ковариациями

(10)

(11)

(12)

Мы говорим, что случайный вектор X был расчленен в (8) на подвекторы так, что вектор

(13)

был расчленен подобным же образом на подвекторы и что матрица

(14)

была таким же образом расчленена на подматрицы

Покажем, что X ⁽¹⁾ и X⁽²⁾ независимы и нормально рас­пределены. Обратная к матрица

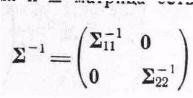⁽¹⁵⁾

Таким образом, квадратичная форма в показателе плотности есть

где

(17)

Отметим также, что Плотность распре­деления X может быть записана следующим образом:

(18)

Частная плотность распределения X ⁽¹⁾ дается в виде интеграла

Таким образом, частное распределение Х⁽¹⁾ будет ; точно так же частное распределение X ⁽²⁾ будет .Значит, совместная плотность распределения Х₁ , ...., X_p является произведением плотности частного распределения

Х₁,…, X_q и плотности частного распределенияХ_q+1, ..., X_р,, поэтому оба множества величин независимы. Если мы имеем некоторое подмножество множества случайных величин, то мы всегда так можем перенумеровать эти величины, что дан­ное подмножество образует Х⁽¹⁾. Этим доказывается доста­точность условия следующей теоремы.

Теорема 2.4.2. Если совместное распределение ве­личин X_l ,…, Х_р нормально, то необходимым и доста­точным условием того, что некоторое подмножество этих величин не зависит от подмножества, состоящего из остальных величин, является равенство нулю всех ковариаций величин одного подмножества и величин другого.

Необходимость следует из того факта, что если X_i из одного подмножества, а X_j из другого, то для любой плот­ности распределения вероятности (см. § 2.2.3)

Так как и (мы молчаливо предпола­гаем, что невырожденная), то условие эквивалентно тому, что . Таким образом, если одно множество ве­личин некоррелировано с остальными величинами, то оба множества являются независимыми. Следует подчеркнуть, что заключение о независимости величин при равенстве нулю их корреляции делается в предположении, что эти величины нормально распределены, но обратное утверждение всегда верно.

Рассмотрим случай двумерного нормального распределения. Тогда Х⁽¹⁾ = Х₁ , Х⁽²⁾ = Х₂,,

и

Поэтому если X₁ и Х₂ имеют двумерное нормальное распределение, то они независимы тогда и только тогда, когда они некоррелированы. Если они некоррелированы, то частное распределе­ние X_i нормально с математическим ожиданием и диспер­сией Приведенное выше рассуждение доказывает также следующее следствие.

Следствие 2.4.1. Если X распределен и если некоторое множество компонент X некоррелировано с другими, компонентами, то частное распределение этого множества является многомерным нормальным распределением со средними значениями, дисперсиями и ковариациями, определяемыми из соответствующих компоненти .

Теперь покажем, что это следствие справедливо также, если два множества не являются независимыми. Мы расчле­нили как и раньше. Произведем невырожденное линейное преобразование подвекторов

(21) (22)

где Т выбирается так, чтобы компоненты Y⁽¹⁾ были некор­релированы с компонентами

У⁽²⁾ =Х^{2). Матрица Т должна удовлетворять уравнению

(23)

Таким образом, и

(24)

Вектор

(25)