Введение в многомерный статистический анализ / page14-58 / ander2_2_2

является результатом невырожденного преобразования X и поэтому распределен нормально с

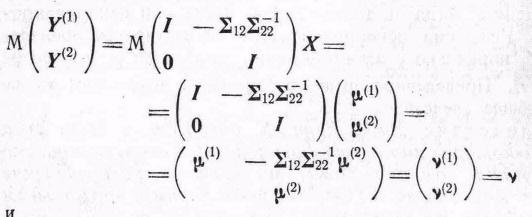(26)

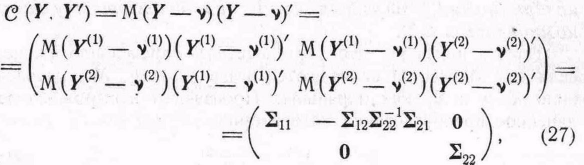
так как

Таким образом, Y⁽¹⁾ и Y⁽²⁾ независимы и, согласно следствию 2.4.1, X⁽²⁾ =Y⁽²⁾ имеет частное распределение Поскольку нумерация компонент X произвольна, мы можем сформулировать следующую теорему.

Теорема 2.4.3. Если X имеет распределение то совместное распределение некоторого множества компонент X является многомерным нормальным рас­пределением со средними значениями, дисперсиями и ко-вариациями, определяемыми из соответствующих компо­нент и .

Рассмотрим преобразование

Z = DX (29)

где Z содержит q компонент, a D — действительная матрица порядка q р. Математическое ожидание Z есть

(30)

а ковариационная матрица есть

(31)

Случай, когда q = р и D не вырождена, был рассмотрен выше. Если q р и D имеет ранг q, то можно найти такую матрицу Е порядка (р—q) p, для которой преобразование

(32)

является невырожденным. Тогда для Z и W существует совместное нормальное распределение и, согласно теореме 2.4.3, частное распределение Z нормально. Таким образом, для матрицы D ранга q (причем X имеет невырожденное распределение, т. е. плотность вероятности) мы доказали следующую теорему.

Теорема 2.4.4. Если X распределен , то Z = DX распределен где D есть матрица порядка q p и ранга q р.

Конец настоящего параграфа посвятим несобственному, или вырожденному, нормальному распределению и распро­странению теоремы 2.4.4 на случай любой матрицы D. Вырожденное распределение есть распределение в p-мерном пространстве, которое концентрируется в подпространстве меньшего числа измерений, т. е. вероятность попадания в мно­жество, не пересекающее подпространства, равна нулю. В слу­чае вырожденного нормального распределения масса сосредо­точена на линейном подпространстве [т. е. на пересечении некоторого числа (р—1)-мерных гиперплоскостей]. Пусть у - множество координат подпространства (число координат равно размерности подпространства), тогда подпространство может быть задано параметрически в виде, где А есть матрица порядка ,а -

p-мерный вектор. Предположим, что Y нормально распределен в q-мерном подпространстве; тогда мы скажем, что

(33)

имеет несобственное, или вырожденное, нормальное распре­деление в p-мерном пространстве. Если MY=v, то. Если , то

Следует заметить, что если р> q, то матрица выро­жденная и не имеет обратной, и поэтому мы не можем написать нормальную плотность для X. В самом деле, X совсем не может иметь плотность распределения, так как из равен­ства нулю вероятности попадания в любое множество, не пере­секающее q-мерного пространства, следует, что плотность распределения вероятностей равна нулю почти всюду.

Теперь заметим, что, наоборот, если среднее значение X равно и ковариационная матрица имеет ранг r, то X можно записать в виде (33) (за исключением нулевой вероят­ности), где X имеет произвольное распределение и Y, состоящий из r (p) компонент, имеет соответствующее распределение. Если имеет ранг r, то имеется невырожденная матрица В порядка такая, что

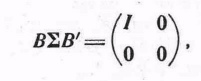(34)

где тождественная матрица имеет ранг r (см. теорему 6 приложения 1).

Преобразование '

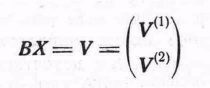(35)

определяет случайный вектор V, ковариационная матрица которого есть (34), а среднее значение

(36)

Так как дисперсии компонент V⁽²⁾ равны нулю, то с вероят­ностью единица .Теперь расчленим так:

(37)

где С состоит из r столбцов. Тогда (35) принимает вид

(38)

Таким образом, с вероятностью единица

(39)

что имеет вид (33) (где С заменяет A, V⁽¹⁾ заменяет Y и заменяет ).

Дадим теперь определение нормального распределения, которое включает и случай вырожденного распределения.

Определение 2.4.1. Говорят, что р-мерный слу­чайный вектор X с и нормально распределен (или распределен), если существует преобразование (33), в котором число строк матрицы А равно р, а число столбцов равно рангу r матрицы и r-мерный .вектор Y имеет невырожденное нормальное распределение с плотностью распределения

(40)

Ясно, что если имеет ранг р, то А можно взять равным I и равным 0; в этом случае X=Y и определение 2.4.1 согласуется с изложенным в § 2.3.

Теорема 2.4.5. Если X распределен , то Z = DX распределен .

Эта теорема включает случаи как невырожденного, так и вырожденного распределения X, a D может быть невыро­жденной и иметь ранг, меньший q. Так как X может быть выражен формулой (33), где Y имеет невырожденное распре­деление , то мы можем написать

, (41)

где DA — матрица порядка . Если ранг DA равен r, то теорема доказана. Если же ранг DA меньше r, например s, то ковариационная матрица величины Z

(42)

имеет ранг s. Согласно теореме 6 приложения 1, существует невырожденная матрица

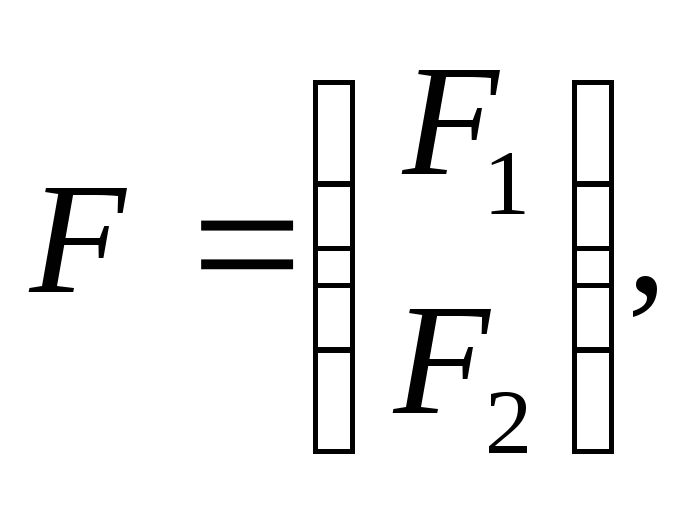(43)

такая, что

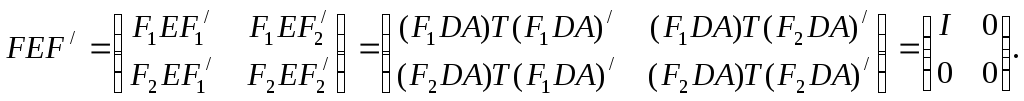(44)

Таким образом, матрица F₁DA имеет ранг s согласно теореме 1, обратной к теореме 1 приложения 1, и матрица F₂DA = 0, так как каждый диагональный элемент (F₂DA) T(F₂DA)' есть квадратичная форма относительно элементов соответствующей строки F₂ DA с положительно определенной матрицей Т. Поэтому ковариационная матрица величины FZ есть (44) и

(45)

Ясно, что U₁имеет невырожденное нормальное распределение. Пусть F ^-1(G₁,G₂). Тогда

(46)

что имеет вид (33). Таким образом, теорема доказана.

Все выводы настоящего параграфа можно проиллюстриро­вать, рассматривая введенную в предыдущем параграфе гео­метрическую интерпретацию. Плотность распределения вероят­ностей величины X постоянна на эллипсоидах (51) § 2.3. Так как преобразование (2) является линейным преобразова­нием (т. е. изменяет оси координат), то плотность распреде­ления Y постоянна на эллипсоидах

(47)

Частное распределение X⁽¹⁾ является проекцией массы распре­деления X в q-мерное пространство первых q координатных осей. Поверхности, на которых плотности распределения постоянны, также являются эллипсоидами. Ясно, что проекция массы на любую прямую нормально распределена.

2.5. Условные распределения и множественный

коэффициент корреляции

2.5.1. Условные распределения. В этом параграфе мы покажем, что условные распределения, полученные из сов­местного нормального распределения, также нормальны. Условные распределения имеют особенно простую природу, так как средние значения зависят от значений фиксированных случайных величин только линейно, а дисперсии и ковариации вообще не зависят от значений фиксированных случайных величин. Теория частной и множественной корреляции, рас­сматриваемая в этом параграфе, была первоначально изложена Пирсоном [1] для трех величин и далее разработана Юлом [1], [2].

Пусть вектор Х_п имеет распределение ( не вы­рождена) и разбит, как и раньше, на два подвектора

(1)

с q и (р — q) компонентами соответственно. Применим здесь алгебраические результаты, изложенные в § 2.4. Совместная плотность распределения вероятностей и есть

Плотность распределения вероятностей X⁽¹⁾ и X⁽²⁾ тогда может быть определена из этого выражения путем подстановки вместо y ⁽¹⁾ и x ⁽²⁾ вместо y ⁽²⁾ (определитель этого преобразования равен 1). Совместная плотность распре­деления вероятностей X⁽¹⁾ и X⁽²⁾ равна

где

(3)

Эта плотность вероятности должна быть . Условная плотность вероятности X⁽¹⁾ при данном значении X⁽²⁾ =x ⁽²⁾ равна частному от деления (2) на значение частной плотности вероятности величины X⁽²⁾ в точке x⁽²⁾, которое равно , т. е. второму множителю в (2). Тогда частное будет равно

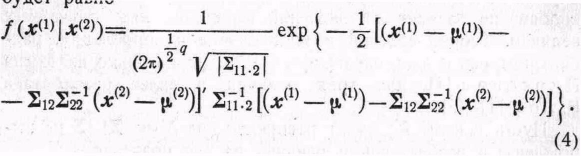
Ясно, что x⁽²⁾ состоит из р — q компонент. Плотность вероят­ности f(x⁽¹⁾|x⁽²⁾) является

q-мерной нормальной плотностью со средним значением

, (5)

и ковариационной матрицей

(6)

Следует заметить, что среднее значение X⁽¹⁾ при данном х⁽²⁾ является просто линейной функцией x⁽²⁾ , а ковариационная матрица Х⁽¹⁾ при данном x⁽²⁾ вообще не зависит от x⁽²⁾.

Определение 2.5.1. Матрица называется матрицей коэффициентов регрессии Х ⁽¹⁾ на x⁽²⁾ .

Элемент i-и строки и j-го столбца матрицы часто обозначается через

Вектор часто называют функцией регрессии.

Пусть является элементом i-й строки и j-го столбца матрицы .Мы назовем его частной ковариацией.

Определение 2.5.2. Выражение

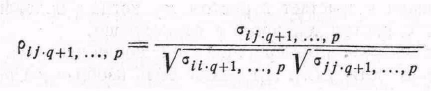(7)

называется частным коэффициентом корреляции между X_i и Xj при фиксированных X_q+l, ..., Х_р.

Нумерация компонент X и число q произвольны. Следо­вательно, это определение