
Введение в многомерный статистический анализ / page14-58 / ander2_3
.docслужит для нахождения условного распределения любых q компонент случайного вектора X, если даны другие р — q компонент. Действительно, можно рассматривать частные распределения некоторых r компонент вектора X и определить условное распределение некоторых q компонент, если даны другие r — q компонент.
Теорема
2.5.1.
Пусть
компоненты вектора X
разделены на две группы, образующие
подвекторы X(1)
и
X(2)
. Допустим,
что среднее значение
![]() подобным
же образом разделено на
подобным
же образом разделено на![]() (1)
и
(1)
и
![]() (2),
и
предположим далее, что ковариационная
матрица
(2),
и
предположим далее, что ковариационная
матрица
![]() вектора
X
разбита на
вектора
X
разбита на![]() 11,
11,
![]() 12,
12,
![]() 22,,которые
являются ковариационными матрицами
соответственно векторов X(1);X(1)
и
X(2);X(2)..
Тогда,
если распределение X
нормально, то условное распределение
Х(1)
при данном X(2)
=
х(2)
также нормально со средним значением
22,,которые
являются ковариационными матрицами
соответственно векторов X(1);X(1)
и
X(2);X(2)..
Тогда,
если распределение X
нормально, то условное распределение
Х(1)
при данном X(2)
=
х(2)
также нормально со средним значением
![]() и
ковариационной матрицей
и
ковариационной матрицей
![]() .
.
В
качестве примера рассмотрим двумерное
нормальное распределение и найдем
условное распределение X1,
при данном Х2
= х2.
В
этом случае
![]()
Таким
образом, матрица порядка (1
![]() 1)
коэффициентов регрессии есть
1)
коэффициентов регрессии есть
![]() и матрица порядка (1
и матрица порядка (1
![]() 1)
частных ковариаций есть
1)
частных ковариаций есть
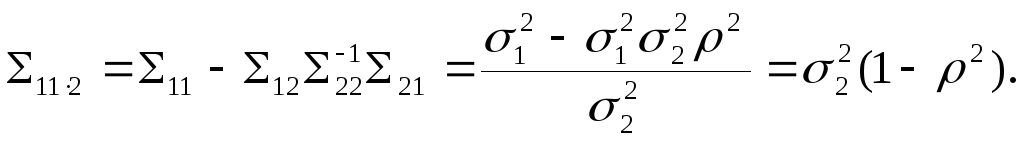 Итак,
плотность распределения
Итак,
плотность распределения
вероятностей Х1 при данном х2 будет
![]()
Следует
отметить, что среднее значение этого
условного распределения возрастает с
ростом х2,
когда
![]() положителен,
и убывает с ростом х2,
когда
положителен,
и убывает с ростом х2,
когда
![]() отрицателен.
отрицателен.
Геометрическая
интерпретация этой теории известна.
Плотность вероятности
![]() может
быть изображена поверхностью
может
быть изображена поверхностью
![]() над
плоскостью (x1
,x2
).
Если
пересечь эту поверхность плоскостью
х2
= с, мы
получим кривую
над
плоскостью (x1
,x2
).
Если
пересечь эту поверхность плоскостью
х2
= с, мы
получим кривую
![]() над
прямой х2
= с
на плоскости (x1
,x2).
Ордината этой кривой пропорциональна
условной плотности распределения
вероятностей Х1
при
данном х2
=
с,
т.
е. она пропорциональна ординате
кривой одномерного нормального
распределения. В более общем случае
удобно рассматривать эллипсоиды
постоянной плотности распределения
вероятностей в р-мерном
пространстве. Поверхности постоянной
плотности распределения
над
прямой х2
= с
на плоскости (x1
,x2).
Ордината этой кривой пропорциональна
условной плотности распределения
вероятностей Х1
при
данном х2
=
с,
т.
е. она пропорциональна ординате
кривой одномерного нормального
распределения. В более общем случае
удобно рассматривать эллипсоиды
постоянной плотности распределения
вероятностей в р-мерном
пространстве. Поверхности постоянной
плотности распределения
![]() являются
пересечениями поверхностей постоянной
плотности
являются
пересечениями поверхностей постоянной
плотности
![]() и гиперплоскостей xq+l
= cq+l
,
..., хр
= ср;
они
также являются эллипсоидами.
и гиперплоскостей xq+l
= cq+l
,
..., хр
= ср;
они
также являются эллипсоидами.
Эти понятия становятся более ясными, если рассматривать реальные совокупности как идеализированно нормально распределенные. Рассмотрим, например, совокупность пар отец — сын. Если эту совокупность разумно считать однородной, то величины роста отцов и величины роста их сыновей приближенно распределены нормально в определенных границах. Условное распределение может быть получено, если рассматривать сыновей, рост отцов которых, скажем, 5 футов и 9 дюймов (в пределах точности измерений); величины роста этих сыновей приближенно распределены нормально. Среднее значение этого нормального распределения отличается от среднего роста сыновей, рост отцов которых, скажем, 5 футов и 4 дюйма, но дисперсии обеих совокупностей равны.
Мы можем также рассматривать тройки наблюдений: рост отца, рост старшего сына и рост второго сына. Распределение величин роста двух сыновей при росте их отцов в 5 футов 9 дюймов является условным распределением двух случайных величин; корреляция между величинами роста старших и вторых сыновей характеризуется частным коэффициентом корреляции. Закрепление роста отцов на постоянном уровне исключает влияние наследственности отцов; однако следует ожидать, что частный коэффициент корреляции будет положительным, так как наследственность по материнской линии и факторы окружающей обстановки вызывают одинаковое изменение роста братьев.
Как
было отмечено выше, любое условное
распределение, полученное из нормального
распределения, также является нормальным
со средним значением, являющимся линейной
функцией фиксированных значений
случайных величин, и постоянной
ковариационной матрицей. В случае, если
распределение не подчинено нормальному
закону, условное распределение одного
множества случайных величин относительно
другого обычно не обладает вышеуказанными
свойствами. Однако можно так построить
распределения величин, не являющихся
нормальными, что некоторые условные
распределения будут обладать этими
свойствами. Это можно сделать, если
взять за плотность распределения X
произведение
![]() где
f(x(2))
—произвольная плотность распределения.
где
f(x(2))
—произвольная плотность распределения.
2.5.2.
Множественный коэффициент корреляции.
Мы
опять рассмотрим вектор X
, разбитый
на Х(1)
и
X(2)
.
Рассмотрим некоторые свойства
![]() Поскольку мы интересуемся только
функциями от ковариации, мы можем
положить
Поскольку мы интересуемся только
функциями от ковариации, мы можем
положить
![]() (т.
е.
(т.
е.
![]() можно
заменить на X).
Выберем
компоненту Хi
вектора
Х(1).
Тогда
можно
заменить на X).
Выберем
компоненту Хi
вектора
Х(1).
Тогда
(8)
(9)
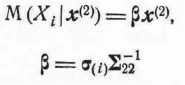
и
![]() есть
i-я
строка
есть
i-я
строка
![]() ,
определяемая из матрицы
,
определяемая из матрицы
![]() (10)
(10)
Рассмотрим
теперь линейную функцию случайного
вектора
![]() Поскольку ковариация между
Поскольку ковариация между
![]() и X(2)
равна
и X(2)
равна
![]() ,
(11)
,
(11)
то
эти две величины независимы. Определим
теперь линейную функцию
![]() ,для
которой
,для
которой
![]() имеет
минимальную дисперсию. Так как MZ2
= MZZ'
для
скаляра Z,
имеет
минимальную дисперсию. Так как MZ2
= MZZ'
для
скаляра Z,
то дисперсия, в силу (11), равна
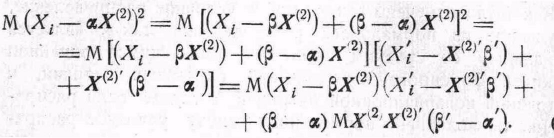 (12)
(12)
Полученный в (12) результат равен
![]() (13)
(13)
Поскольку
![]() положительно определена, то второе
слагаемое в (13) неотрицательно и достигает
минимума (то есть 0), когда
положительно определена, то второе
слагаемое в (13) неотрицательно и достигает
минимума (то есть 0), когда
![]() .
Таким образом, регрессия, является
функцией Х(2)
такой,
что дисперсия
.
Таким образом, регрессия, является
функцией Х(2)
такой,
что дисперсия
![]() минимальна.
минимальна.
Покажем
теперь, что максимум корреляции между
Xi
и
![]() достигается
при
достигается
при
![]() .Известно,
что
.Известно,
что
![]() (14)
(14)
для
некоторых с
и
![]() .
Отсюда
.
Отсюда
![]() (15)
(15)
Таким образом,
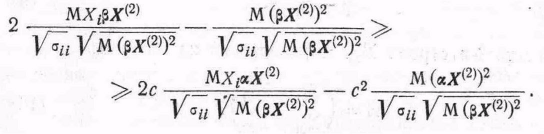 (16)
(16)
Пусть теперь
![]() (17)
(17)
Тогда (16) может быть представлено следующим образом:
![]() (18)
(18)
Этим закончено доказательство следующей теоремы.
Теорема
2.5.2.
Пусть
X
распределен
![]() ;
;
![]() и
и
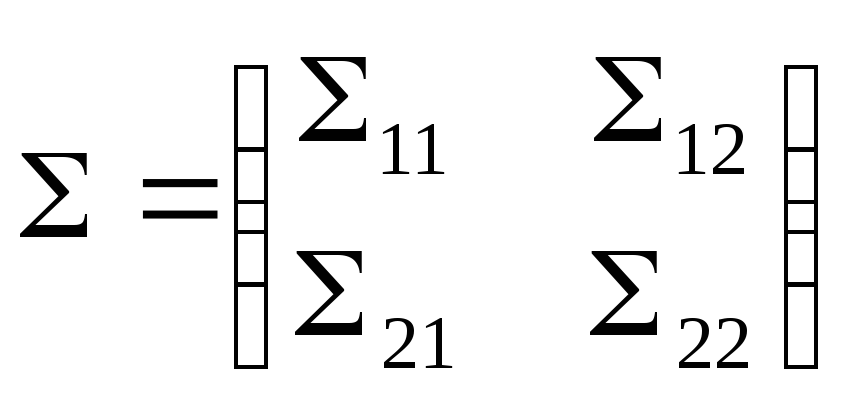 ,а
,а
![]() обозначает
i-ю
строку
обозначает
i-ю
строку
![]() .Из
всех линейных комбинаций
.Из
всех линейных комбинаций
![]() линейная,
комбинация
линейная,
комбинация
![]() дает минимум дисперсии
дает минимум дисперсии
![]() и
максимум корреляции между Хi
и
и
максимум корреляции между Хi
и
![]() .
.
Определение
2.5.3.
Максимальное
значение корреляции между Xi
и линейной комбинацией
![]() называется множественным коэффициентом
корреляции между Xi
и Х(2)
и
обозначается через
называется множественным коэффициентом
корреляции между Xi
и Х(2)
и
обозначается через
![]() .
Из
этого определения следует
.
Из
этого определения следует
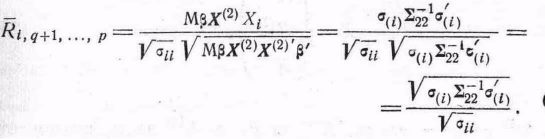 (19)
(19)
Полезна формула
![]() '
(20) где
'
(20) где
![]() (21)
(21)
Поскольку
![]() ,
(22)
,
(22)
отсюда следует, что
![]() . (23)
. (23)
Это,
между прочим, показывает, что никакая
условная дисперсия компоненты X
не
может быть больше ее безусловной
дисперсии. Действительно, из формулы
(23) видно, что с увеличением
![]() уменьшается
условная дисперсия.
уменьшается
условная дисперсия.
2.5.3. Некоторые формулы для частных коэффициентов корреляции. Рассмотрим теперь отношения между несколькими условными распределениями, полученными фиксированием нескольких различных множеств случайных величин. Эти отношения полезны, поскольку они позволяют определить одно множество параметров условного распределения по другому. Частным случаем является
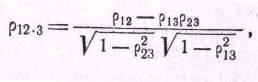 (24)
(24)
это следует из (7), когда р = 3 и q = 2. Получим теперь обобщение этого результата. Вывод довольно скучный, но он дается здесь для полноты изложения. Пусть
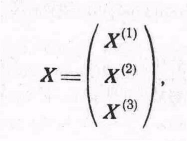 (25)
(25)
где
X(1)
состоит
из р1
,
Х{2)
из
р2
, а
Х
(3)
из
р3
компонент.
Допустим, что нам задано условное
распределение X
(1)
и
X
(2)
при
данном X(3)
=
x(3)
;
как найти условное распределение Х(1)
при
данных Х(2)
= х(2)
и Х(3}
=
x(3).
Нам известно, что условное среднее
значение и ковариация
![]() будут
будут
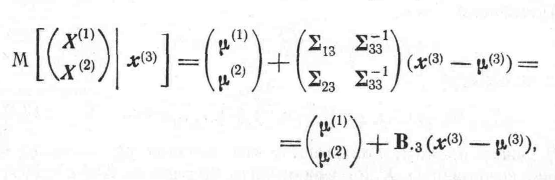 (26)
(26)
и
 (27)
(27)
Подобным же образом
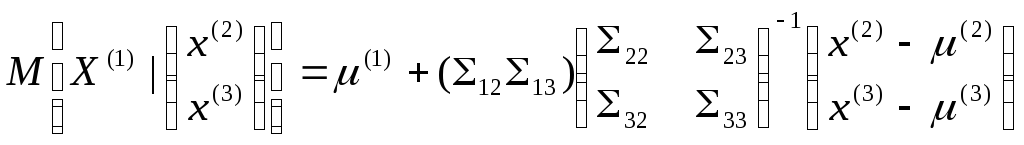 .
(28)
.
(28)
 .
(29)
.
(29)
Выразим теперь (28) и (29) в обозначениях (26) и (27).
Будем
рассматривать распределение
![]() при
данном х(3)
при
данном х(3)
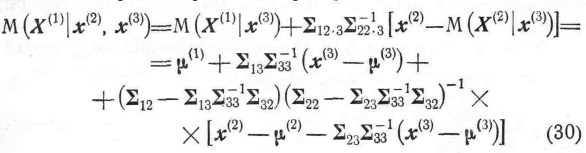 как
многомерное нормальное распределение.
Мы знаем, что
как
многомерное нормальное распределение.
Мы знаем, что
и
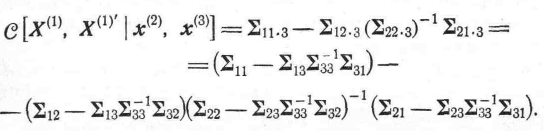 (31)
(31)
Известно, что формулы (28) и (30), а также формулы (29) и (31) являются одними и теми же. Это можно проверить также алгебраически.
В частности, при p1=q, p2=1 и р3 = р – q - 1 мы получим
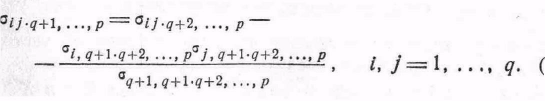 (32)
(32)
Поскольку
![]() ,
(33)
,
(33)
мы получим
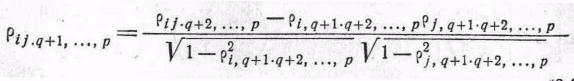 (34)
(34)
Это полезная формула для последовательного определения
![]() по
по
![]() .
.
2.6. Характеристическая функция; моменты
2.6.1. Характеристическая функция. Характеристическая функция многомерного нормального распределения имеет вид, подобный плотности распределения вероятности. Моменты и семиинварианты легко вычисляются по характеристической функции.
Определение 2.6.1. Характеристическая функция
![]() (1)
(1)
случайного вектора X определена для каждого действительного вектора t.
Для разъяснения этого определения следует сперва дать представление о математическом ожидании комплексной функции случайного вектора.
Определение 2.6.2. Пусть комплексная функция g (х) записана в виде
g (х) = g1(х)+ ig2 (х), где g1 (х) и g2(x) — действительные функции. Тогда математическое ожидание g(X) равно
Mg(X) = Mg1(X) + iMg2(X). (2) В частности,
![]() (3)
(3)
Для оценки характеристической функции вектора X часто бывает удобно применить следующую лемму:
Лемма
2.6.1.
Пусть![]() .
Если X(1)
и Х(2)
независимы
и
.
Если X(1)
и Х(2)
независимы
и
![]() то
то
![]() . (4)
. (4)

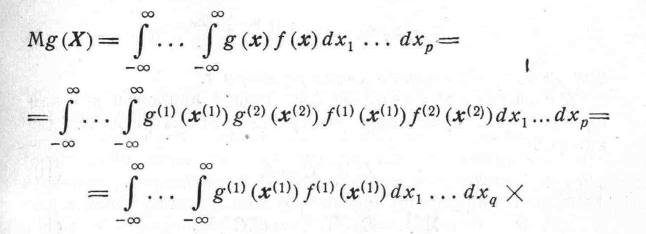
(5)
Если g(x) комплексна, то
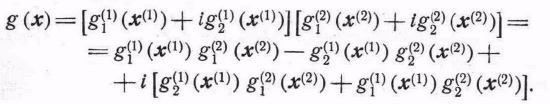 (6)
(6)
Тогда
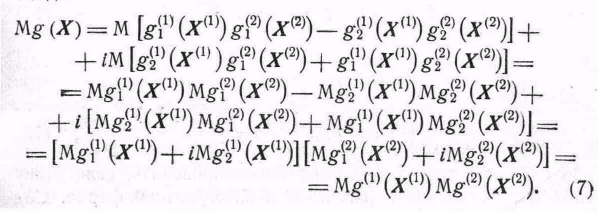
Если
применить лемму 2.6.1 к
![]() ,
то
получится Лемма 2.6.2. Если
компоненты X
независимо распределены, то
,
то
получится Лемма 2.6.2. Если
компоненты X
независимо распределены, то
![]() (8)
(8)
Найдем теперь характеристическую функцию Нормально распределенного случайного вектора.
Теорема
2.6.1.
Характеристическая
функция вектора X,
распределенного![]() ,
равна
,
равна
![]() (9)
(9)
для любого действительного вектора t.
Доказательство. Из следствия 4 приложения 1 нам известно, что существует невырожденная матрица С, для которой
![]() (10)
Тогда
(10)
Тогда
![]() (11)
(11)
Пусть
![]() (12)
(12)
Тогда Y распределен N(0, I).
Характеристическая функция Y равна
![]() (13)
(13)
Поскольку
![]() распределена
распределена
![]() то
то
![]() (14)
(14)
Таким образом,
 ,
(15)
,
(15)
ибо
![]() ;
третье равенство легко проверить, если
написать обе части этого равенства
в интегральной форме. Согласно (11),
получим
;
третье равенство легко проверить, если
написать обе части этого равенства
в интегральной форме. Согласно (11),
получим
![]() (16)
(16)
что доказывает теорему.
Характеристическая функция нормального распределения очень полезна. Ясно, что мы можем применить указанный метод доказательства для получения результатов § 2.4. Если
Z = DX, то характеристическая функция Z есть
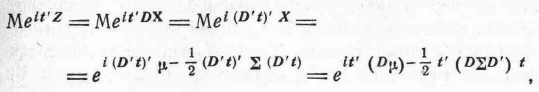 (17)
(17)
что
является характеристической функцией
![]() (согласно
теореме 2.6.3).
(согласно
теореме 2.6.3).
Интересно использовать характеристическую функцию для того, чтобы показать, что только для многомерного нормального распределения любая линейная комбинация случайных величин распределена нормально. Рассмотрим p-мерный вектор Y с плотностью распределения вероятностей f(y) и характеристической функцией
 (18)
(18)
и
допустим, что среднее значение Y
есть
![]() и
ковариационная матрица есть
и
ковариационная матрица есть
![]() .
Допустим также, что величина u'Y
нормально
распределена для каждого и.
Тогда
характеристическая функция такой
линейной комбинации будет
.
Допустим также, что величина u'Y
нормально
распределена для каждого и.
Тогда
характеристическая функция такой
линейной комбинации будет
![]() (19)
(19)
Пусть
теперь t=l.
Поскольку
правая часть (19) является характеристической
функцией
![]() ,
то доказательство завершено (см. теорему
2.6.3).
,
то доказательство завершено (см. теорему
2.6.3).
Теорема 2.6.2. Если всякая линейная комбинация компонент вектора Y распределена нормально, то Y также распределен нормально.
Можно
было бы мимоходом заметить, что для
справедливости теоремы 2.6.2 существенно,
чтобы всякая
линейная
комбинация была распределена нормально.
Например, если
![]() и
Y1
и
Y2
не являются независимыми, то каждая
из Y1
и Y2
может иметь частное нормальное
распределение, а распределение Y
может
не быть нормальным. Легче всего это
проиллюстрировать на геометрическом
примере.
и
Y1
и
Y2
не являются независимыми, то каждая
из Y1
и Y2
может иметь частное нормальное
распределение, а распределение Y
может
не быть нормальным. Легче всего это
проиллюстрировать на геометрическом
примере.
Пусть совместное распределение Х1, Х2 нормально со средним значением, равным нулю. Переместим ту же массу в границах рис. 1 от прямоугольника А к С и от В к D. Мы увидим, что результирующее распределение F таково, что частные распределения Yl и Y2 такие же, как и частные распределения соответственно Х1 и Х2, которые являются нормальными, и тем не менее совместное распределение Yl и Y2 не нормально.
Этот пример может быть использован также для доказательства того, что две величины
Yl и Y2 могут быть некоррелированными, и частное распределение каждой из них может быть нормально, но совместное распределение Y1 и Y2 не обязательно нормально и эти величины не обязательно независимы. Чтобы показать это, надо выбрать прямоугольники так, чтобы для результирующего распределения математическое ожидание Yl Y2 было равно нулю. Геометрически ясно, что это может быть сделано.
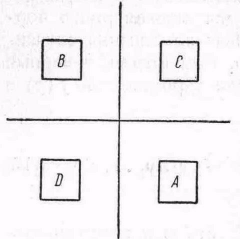 Рис.
1.
Рис.
1.
Для будущего мы установим две полезные теоремы, относящиеся к характеристическим функциям.
Теорема
2.6.3. Если
случайный вектор X
имеет плотность распределения вероятностей
f
(х) и характеристическую функцию
![]() ,
то
,
то
 (20)
(20)
Отсюда видно, что характеристическая функция однозначно определяет плотность распределения вероятностей. Если же плотность вероятности для X не существует, то характеристическая функция однозначно определяет распределение вероятности для любого «интервала непрерывности». В одномерном случае интервал непрерывности—это интервал, в котором функция распределения не имеет разрывов на концах.
Теорема
2.6.4.
Пусть
![]() -последовательность
функций распределения, a
-последовательность
функций распределения, a![]() —последовательность
соответствующих характеристических
функций. Необходимым и достаточным
условием сходимости
—последовательность
соответствующих характеристических
функций. Необходимым и достаточным
условием сходимости
![]() к
функции распределения
к
функции распределения
F
(х) является сходимость
![]() к
к
![]() для каждого t,
где
для каждого t,
где
![]() непрерывна
при t
=0. Если это условие соблюдается, то
предел
непрерывна
при t
=0. Если это условие соблюдается, то
предел
![]() есть
характеристическая функция для
предельного распределения F(x).
есть
характеристическая функция для
предельного распределения F(x).
С доказательством этих двух теорем читатель может ознакомиться по книге Крамера [2], §§ 10.6, 10.7.
2.6.2. Моменты и семиинварианты. Моменты величин X1, ..., Xp с совместным нормальным распределением могут быть получены из характеристической функции (9). Среднее значение равно
![]() (21)
(21)
Второй момент есть
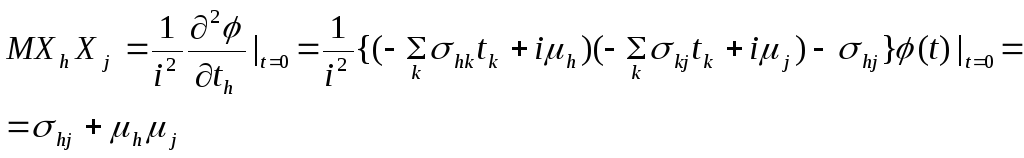 (22)
(22)
Таким образом,
![]() (23)
(23)
![]() (24)
(24)
Любой третий центральный момент равен
![]() (25)
(25)
Четвертый центральный момент равен
![]() (26)
(26)
Определение 2.6.З. Если все моменты распределения существуют, то семиинварианты равны коэффициентам k в разложении
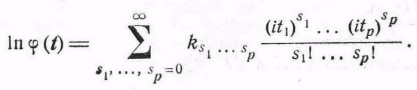 (27)
(27)
В случае многомерного нормального распределения
![]()
Семиинварианты,
для которых![]() ,
обращаются в нуль.
,
обращаются в нуль.
ЛИТЕРАТУРА
§ 2.2. Кен да л л [3], стр. 19—22, 79—81, 104—105; Колмогоров [1]; Крамер [2], стр. 260—270, 291—297; Муд [2], стр. 74—86, 102—103; Уилкс [10], стр. 5—40.
§ 2.3. Дэвид [3]; К е н д а л л [2], [3], стр. 22, 79—80, 89 133-134, 376-378; Кэдуел [1]; Муд [2], стр. 165-170, 176-180; К. Пирсон [6], [7]; Плакетт [2J; Пойа [1]; Уилкс [10], стр. 59—68.
г § 2.4. Крамер [2], стр. 312-313; Муд [2], стр. 181; Уилкс [10], стр. 68—71.
§ 2.5. К е н д а л л [3], стр. 334—335; 368—376, 380—381; Крамер [2], стр. 305-308, 314-316; Муд [2], стр. 181-184; К Пирсон [1]; Уилкс [10], стр. 40—46; 71; Юл [1], [2].
§ 2.6. К е н д а л л [3], стр. 79—80; Крамер [2], стр. 100—103, 310-311, 376-378; Кук [1], [2]; Муд [2], стр. 184-186
Ко всей главе 2. Бирнбаум [1]; Вашвани [1]; Гне-денко [1]; Джонсон [1]; Камат [1]; Кансадо [11; Мак-Фа дден И]; Мор а н [2]; Набейя[1]; ОбергП]; Скито-вич[1]; Филлер, Льюис и Пирсон [1].
