3.3.2. Распределение параметров

Хотя требуемая плотность p(х) неизвестна, предположим, что она имеет известную параметрическую форму. Единственно, что предполагается неизвестным, это величина параметрического век­тора . Тот факт, что р(х) неизвестна, но имеет известный парамет­рический вид, выразим утверждением, что функция p(x|) полно­стью известна. При байесовском подходе предполагается, что неизвестный параметрический вектор есть случайная переменная. Всю информацию о до наблюдения выборок дает известная апри­орная плотность p(). Наблюдение выборок превращает ее в апо­стериорную плотность p(|), которая, как можно надеяться, имеет крутой подъем вблизи истинного значения .

Основная наша цель—это вычисление плотности p(x|), до­статочно достоверной для того, чтобы прийти к получению неиз­вестной p(х). Это вычисление мы выполняем посредством интегри­рования объединенной плотности р(х, |) по . Получаем

=

причем интегрирование производится по всему пространству пара­метра ⁶. Теперь р(х, |) всегда можно представить как произве­дение р(х, |). Так как х и выборки из получаются независимо, то первый множитель есть просто p(x|). Распределе­ние величины х, таким образом, полностью известно, если известна величина параметрического вектора. В результате имеем

p(x|) = (14)

Это важнейшее уравнение связывает «условную по классу» плот­ность p(x|) с апостериорной плотностью p(|) неизвестного па­раметрического вектора. Если вблизи некоторого значения функ­ция p(|) имеет острый пик, то p(x|)  p(x|), так что решение может быть получено подстановкой оценки в качестве истинной величины вектора параметров. Вообще, если существует большая неопределенность относительно точного значения , это уравнение приводит к средней плотности p(x\) по возможным значениям . Таким образом, в случае, когда неизвестные плотности имеют из­вестный параметрический вид, выборки влияют на p(x\) через апостериорную плотность р(|).

3.4. Обучение при восстановлении среднего значения нормальной плотности

3.4.1. Случай одной переменной: p(|)

В данном разделе мы рассмотрим вычисление апостериорной плотности p(|) и требуемой плотности р(x|) для случая, когда р(x |)~N(,), а вектор среднего значения есть неизвестный вектор параметров. Для простоты начнем с одномерного случая, при котором

р(x |)~N(,), (15)

где единственной неизвестной величиной является среднее значение . Предположим, что любое исходное знание, которое мы можем иметь о, можно выразить посредствомизвестной априорной плот­ности р(). Кроме того, можно предположить, что

p()~N(,), (16)

где и известны. Грубо говоря, величинаесть наше лучшее исходное предположение относительно, аотражает неуверен­ность в отношении этого предположения. Предположение о том, что априорное распределение для нормальное, в дальнейшем упростит математические выражения. Однако решающее предположение за­ключается не столько в том, что априорное распределениенор­мально, сколько в том, что оно существует и известно.

Выбрав априорную плотность для , можно представить ситу­ацию следующим образом. Вообразим, что величина , получена из множества, подчиняющегося вероятностному закону р(). Будучи однажды получена, эта величина представляет истинное значение и полностью определяет плотность для х. Предположим теперь, что из полученного множества независимо взято п выборок x₁, . . . , x_n. Положив ={x₁, . . . , x_n}, воспользуемся байесовским правилом, чтобы получить выражение

(17)

где — масштабный множитель, зависящий от , но не зависящий от . Из этого уравнения видно, как наблюдение выборочного мно­жества влияет на наше представление об истинном значении , «превращая» априорную плотность р() в апостериорную плот­ностьp(|). Так как p(x_k|)N(,) иp()N(,) то имеем

(18)

где множители, не зависящие от , включены в константы и. Таким образом, p(|), представляющая собой экспоненциальную функцию квадратичной функции от , также является нормальной плотностью. Так как это остается в силе для любого числа выборок, тоp(|) остается нормальной, когда число п выборок возрастает, и p(|) называют воспроизводящей плотностью. Если восполь­зоваться p(|)~N(,), то значенияимогут быть найде­ны приравниванием коэффициентов из уравнения (18) соответствую­щим коэффициентам из выражения

p(|) = (19)

Отсюда получаем

(20)

и

, (21)

где m_n есть выборочное среднее

. (22)

Решая уравнения в явном виде относительно и, получаем

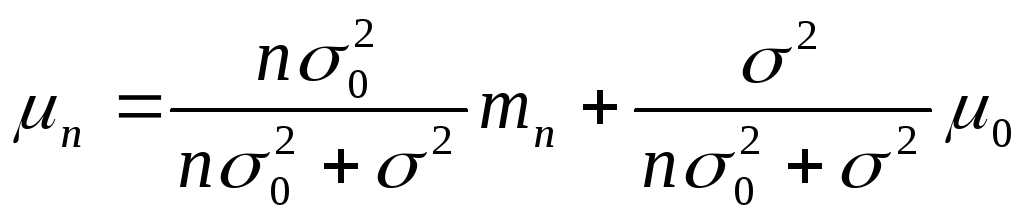(23)

и

. (24)

Из этих уравнений видно, как комбинация априорной информа­ции и эмпирической информации выборок дает апостериорную плот­ность p(|). Грубо говоря, представляет наше лучшее предпо­ложение относительно после наблюдения п выборок, а отражает нашу неуверенность относительно этого предположения. Так как монотонно убывает с ростом n, стремясь к /п при стремлении п к бесконечности, каждое добавочное наблюдение уменьшает нашу неуверенность относительно истинного значения . При возраста­нии п. функция p(|) все более заостряется, стремясь к дельта-функции при n. Такое поведение обычно называется байесов­ским обучением (рис. 3.2).

Рис. 3.2. Обучение среднему при нормальной плотности.

Вообще представляет линейную комбинациюm_n и с неот­рицательными коэффициентами, сумма которых равна единице. Поэтому значение , всегда лежит между m_n и . Приве­личинастремится к выборочному среднему при стремлениип к бесконечности. Если , то получаем вырожденный случай, при котором априорная уверенность в том, что =, настолько тверда, что никакое число наблюдений не сможет изменить нашего мнения. При другой крайности, когда, мы настолько не уве­рены в априорном предположении, что принимаем=m_n , исходя при оценке только из выборок. Вообще относительный баланс ме­жду исходным представлением и опытными данными определяется отношением к , называемым иногдадогматизмом. Если дог­матизм не бесконечен, то после получения достаточного числа вы­борок предполагаемые конкретные значения ине играют роли, астремится к выборочному среднему.