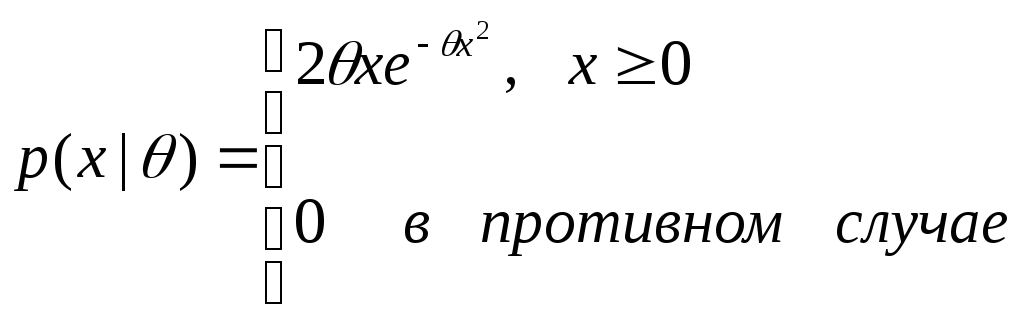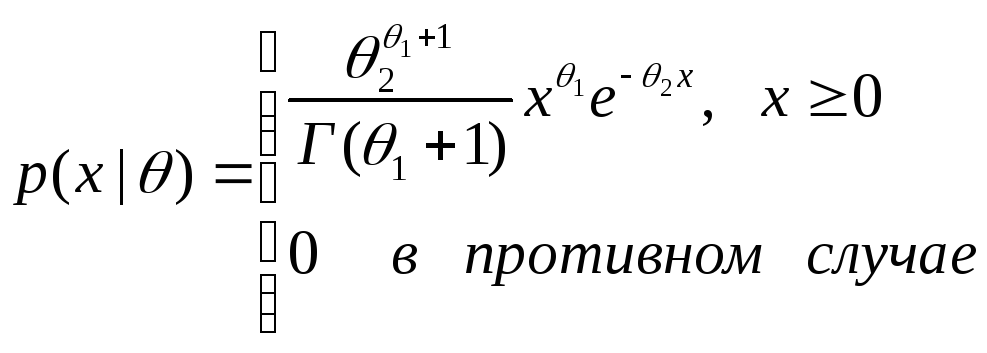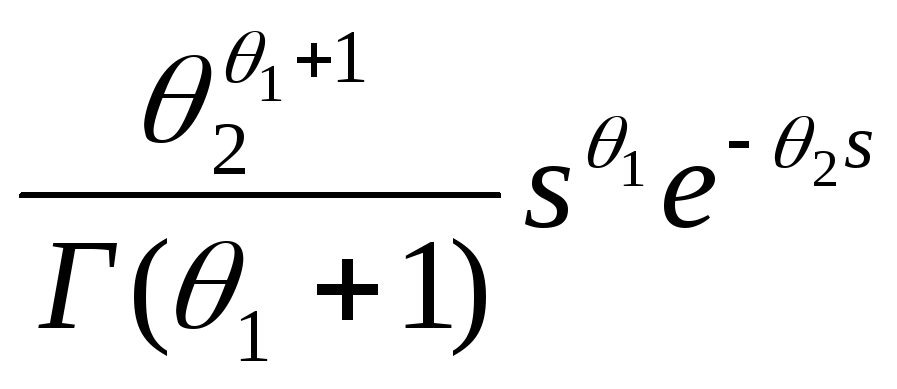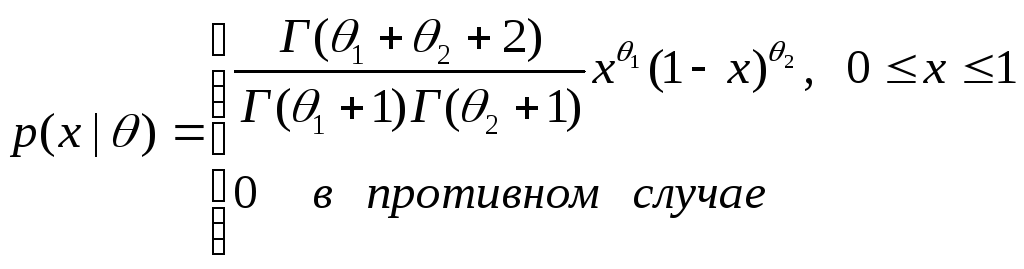3.7. Достаточные статистики и семейство экспоненциальных функций

Рассмотрим применение теоремы факторизации для получения достаточных статистик на примере хорошо знакомого случая нор­мального распределения при p(x|)~N(,). Имеем

В этом разложении первый множитель выделяет зависимость p(|) от , а согласно теореме факторизации, видно, что статистика достаточна для . Конечно, любая взаимно однозначная функция этой статистики также достаточна для , в частности и выборочное среднее

также достаточно для . Исходя из этой статистики, можно написать

g(m_n, )=.

Воспользовавшись формулой (38) или непосредственной подста­новкой, можно получить ядро плотности

Из этого выражения сразу же выясняется, что m_n и есть оценка по максимуму правдоподобия для . Байесовскую апостериорную плотность можно получить из (m_n, ), выполняя интегрирование согласно (39). Если априорная плотность близка к равномерной, то р (|) = (m_n, ).

Такой же общий подход возможен и при определении достаточ­ных статистик для других функций плотности. В частности, он применим к любому из членов экспоненциального семейства, группы функций распределения и плотностей, имеющих простые достаточ­ные статистики. В число членов экспоненциального семейства вхо­дят нормальное, экспоненциальное, релеевское, пуассоновское и многие другие известные распределения. Все они могут быть запи­саны в виде

р(х|) =(x)exp[a()+b()^tc(x)] (40)

Таким образом, получаем

(41)

где можно принять

(42)

g(s, )=exp[n{a()+b()^ts}] (43)

и

. (44)

Выражения функций распределения, достаточных статистик и ненормированных ядер для некоторых обычно встречающихся чле­нов экспоненциального семейства приведены в табл. 3.1.Вывод из этих выражений оценок по максимуму правдоподобия и байесов­ских апостериорных распределений вполне обычная вещь. Выраже­ния, за исключением двух, приведены для случая одной переменной, хотя и могут быть использованы для случаев с многими перемен­ными, если можно допустить статистическую независимость¹¹.

Общий вид распределений из экспоненциального семейства
Наименование	Распределение	Область определе­ния	s		[g (S, )]^1/n
Нормальное, с одной пере­менной		>0
Нормальное, с многими переменны-ми		положи-тельно опреде-лена
Экспоненци­альное		>0
Релея		>0
Максвелла		>0
Гамма		>-1 >0
Бета		>-1 >-1
Пуассона		>0
Бернулли		0<<1
Биномиальное	, x=0,1,. . .,m	0<<1
Полино-миаль­ное		0<<1

Было бы приятно отметить в заключение, что полученные резуль­таты составляют набор средств, достаточный для решения большин­ства задач из области классификации образов. К сожалению, все обстоит иначе. В применении ко многим случаям указанные члены экспоненциального семейства с их плавным изменением и однооб­разием формы не представляют хорошего приближения реально встречающихся плотностей. Часто применяемое упрощающее пред­положение о статистической независимости далеко не всегда ока­зывается справедливым. В случае, когда применение функции из экспоненциального семейства и дает хорошее приближение неиз­вестной плотности, обычно бывает необходимо оценивать множество неизвестных параметров, а в распоряжении имеется только огра­ниченное число выборок. Как мы увидим, это может привести к тому, что оптимальные оценки дадут малоудовлетворительные ре­зультаты, и даже к тому, что «оптимальные» системы будут выпол­нять свои функции хуже, нежели «почти оптимальные».