Дифференциальные уравнения
1. Задачи, приводящие к понятию дифференциального уравнения
При изучении явлений природы, науки и техники приходится решать задачи, в которых устанавливается связь между самой переменной и функцией, переменной и ее производной.
Материальная точка движется со скоростью
,
пропорционально
.
Найти закон движения
.
Из условий задачи
,
где
коэффициент
пропорциональности, следовательно,
получаем
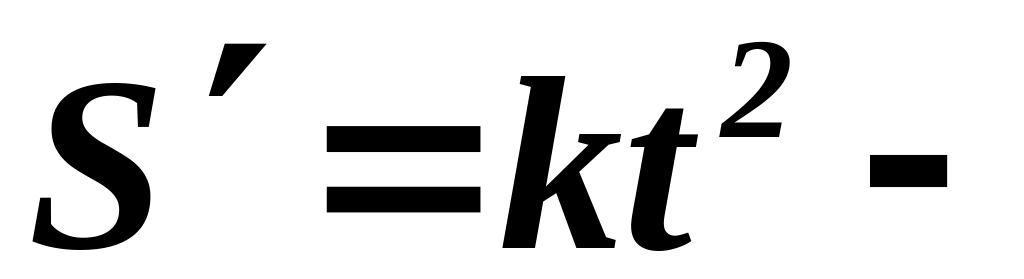дифференциальное
уравнение.Найти кривую, в каждой точке которой угловой коэффициент касательной равен удвоенной абсциссе соответствующей точки.
Если
искомая
кривая, то из геометрического смысла
производной следует, что
дифференциальное
уравнение.
Замечание. Из
дифференциального исчисления известно,
что дифференциалы функции
,
т.е. производная равна отношению
дифференциала функции к дифференциалу
независимой переменной.
Следовательно, можно переписать дифференциальные уравнения в задачах 1) и 2):
к первому примеру: ко второму примеру:
2. Основные понятия дифференциальных уравнений
Определение. Равенство,
которое устанавливает зависимость
между независимой переменной
,
искомой функцией
и ее производной
или дифференциалами, называется
дифференциальным
уравнением.
Пример
1.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной или дифференциала, входящих в это уравнение.
Определение. Степенью дифференциального уравнения называется наивысшая степень старшей производной или дифференциала, входящих в это уравнение.
Пример
2.
уравнение
второго порядка и третьей степени.
Дифференциальное
уравнение п
- го порядка
в общем виде записывается так:
;
(1)
Определение. Функция
называется решением уравнения (1), если
при подстановке ее в это уравнение оно
обращается в тождество относительно
независимой переменной х.
Пример
3.
является
решением уравнения
,
т.е.
верно.
Нетрудно проверить,
что функция
также является решением дифференциального
уравнения. Таким образом, данное уравнение
имеет бесконечно много решений. Основная
задача теории дифференциальных уравнений
найти все решения данного дифференциального
уравнения. Процесс
отыскания решения
называется его интегрированием.
3. Дифференциальные уравнения I порядка
Общий вид дифференциального уравнения I порядка:
(1)
Если уравнение
(1) можно разрешить относительно
производной, то его можно переписать:
(2)
Определение. Функция
,
дифференцируемая по
и непрерывная по
,
где
,
называется общим
решением
уравнения (1), если выполняются условия:
для любого
эта функция является решением (1);когда пробегает весь интервал
,
мы получаем все решения данного
уравнения.
Определение. Частным решением уравнения (1) называется любое его решение, которое получается из общего решения при фиксированном .
Геометрический смысл общего и частного решений
Пусть функция
есть общее решение уравнения (1).
Зафиксируем
,
тогда получим функцию одного переменного
.
График этой функции называется
интегральной
кривой.
Если
изменить, то получим семейство интегральных
кривых.
Вернемся к задачам 1) и 2) и построим интегральные кривые:
общее
решение дифференциального уравнения.
При
,
задавая
,
получим кубические параболы следующего
вида:
общее
решение дифференциального уравнения.
Замечание. Не всегда при интегрировании решение дифференциального уравнения получается в явном виде.
Чаще всего, это решение имеет
в
ид:
и называется общим
интегралом
данного
дифференциального уравнения.