8.3Оценка коэффициентов передаточной функции с помощью гармонических входных воздействий

Гармонические входные воздействия описываются выражением:

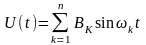, (8.16)

где 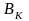, 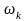– амплитуда и частота к-ой гармонической составляющей (к=1,2….n).

Выходной сигнал Х(t) будет представлять сумму частотных составляющих, отличающихся амплитудой и фазой:

, (8.17)

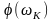где – амплитудная частотная характеристика;

– фазовая частотная характеристика.

Пусть передаточная функция объекта известна и в общем виде представляет собой отношение многочленов:

. (8.18)

Производя замену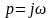 перейдем к комплексной частотной характеристике:

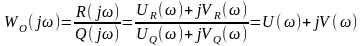. (8.19)

Выделим из этого выражения правую часть:

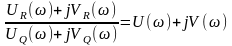. (8.20)

Отсюда определим действительную и мнимую части числителя:

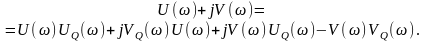. (8.21)

Сравнив действительную и мнимую части, получим два уравнения:

(8.22)

Для решения системы (8.22) необходимо экспериментально определить вещественную и мнимую части частотной характеристики объекта и .

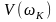Подавая на вход объекта управляющие воздействия 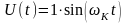, получим выходные сигналы:

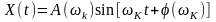. (8.23)

Тогда вещественную и мнимую части можно определить либо через амплитудную и фазовую частотные характеристики

; (8.24)

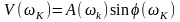, (8.24)

либо с помощью фильтра Фурье, реализованного программно в соответствии с выражениями

; (8.25)

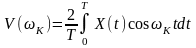, (8.26)

гдеТ – время усреднения результатов вычислений.

В результате экспериментов получим 2n значений, которые используем в системе (8.22). Неизвестные коэффициенты и можно определить путем решения n систем уравнений.

Пример 8.2 Идентификация параметров электромеханической системы по частотным характеристикам

Исходные данные:

1. Передаточная функция объекта:

.

2. Значения постоянных: k = 15, a₀ = 0,03, a₁ = 0,03.

Решение:

1. Составляем структурную схему исследования математической модели с использованием пакета Simulink в среде MATLAB (рис. 8.8).

Рисунок 8.8 – Схема исследования математической модели в пакете MatLabSimulink

Параметры настройки модели:

– Время моделирования – 0,0 ÷ 10,0 с;

– Амплитуда синусоидального сигнала – 1,0;

– Постоянная составляющая (Bias) – 0,0;

– Частота (Frequency) – 1,0; 5,0; 10,0 с^-1;

– Мультиплексор – 2 входа, способ отображения – bar;

Результаты исследований идеальной и реальной переходной характеристики, а также амплитудно-частотной и фазо-частотной характеристик выходного сигнала при различных частотах управляющего сигнала приведены на рис. 8.9–8.11.

Рисунок 8.9 – Идеальная и реальная переходная, амплитудно-частотная и фазо-частотная характеристики выходного сигнала при частоте

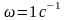
Обработка результатов математического моделирования проводится в следующей последовательности.

Входной сигнал описывается выражением

,

где .

Выходной сигнал Х(t):

.

Отношение этих сигналов определяется передаточной функцией объекта:

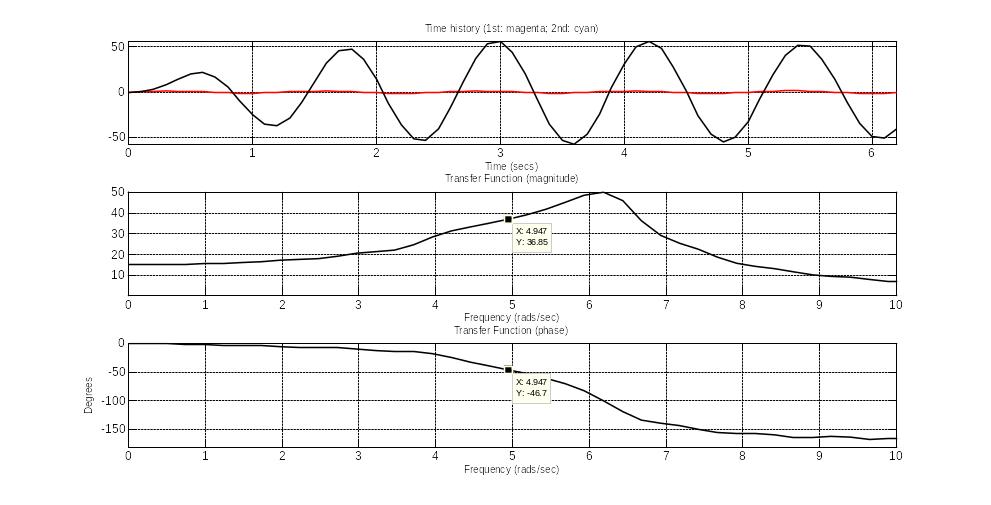
Рисунок 8.10 – Идеальная и реальная переходная, амплитудно-частотная и фазо-частотная характеристики выходного сигнала при частоте

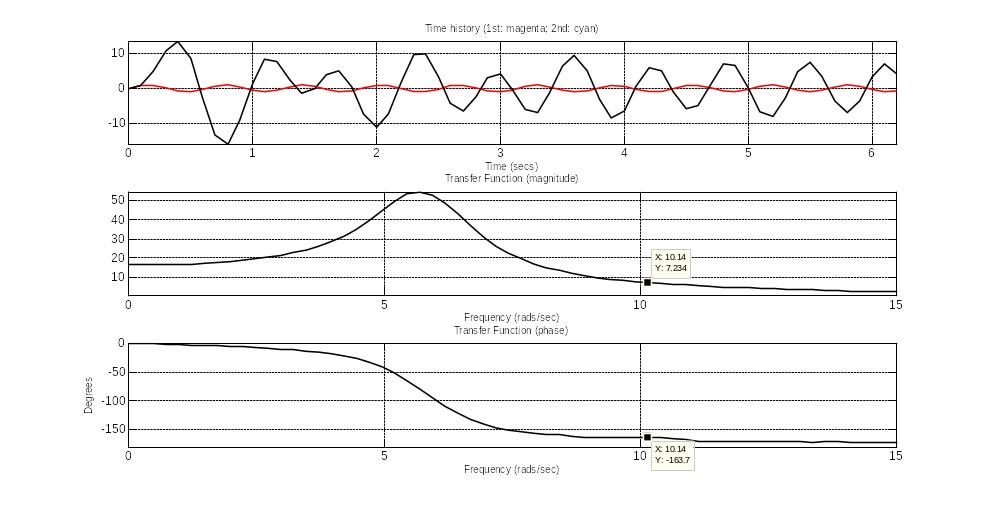
Рисунок 8.11 – Идеальная и реальная переходная, амплитудно-частотная и фазо-частотная характеристики выходного сигнала при частоте

.

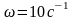
В общем случае передаточная функция при переходе к полярным координатам (амплитудно-фазовой характеристике) описывается отношением комплексных функций числителя (R) и знаменателя (Q) или представляется в комплексной форме следующим образом:

.

Отсюда числитель:

.

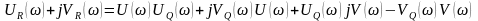После группирования вещественной и мнимой составляющих получим:

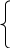
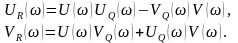
Из графиков на рис. 8.9–8.11 определяем:

1. ₁= 1 с^-1, А₁=15.13, ₁= –3,089;

2. ₂= 5 с^-1, А₂=36.85, ₂= –46.7;

3. ₃= 10 с^-1, А₃=7,234, ₃= –163,7.

Определяем вещественные и мнимые характеристики объекта в этих точках:

1. ₁= 1 с^-1:

,

.

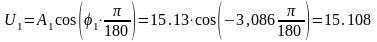2. ₂= 5 с^-1:

,

.

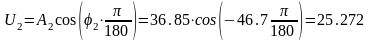3. ₃= 10 с^-1:

,

.

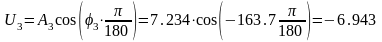Определяем вещественные и мнимые характеристики числителя и знаменателя АФХ объекта:

.

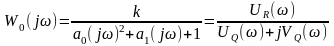Здесь:

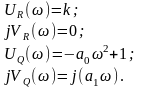
Составляем систему уравнений для каждого из трех экспериментальных результатов:

w₁= 1 с^-1:

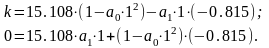
w₂= 5 с^-1:

w₃= 10 с^-1:

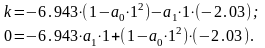
С применением пакета MathCad определяем решение системы уравнений при w₁= 1 с^-1 и w₃= 10 с^-1 относительно k, а₀, а₁:

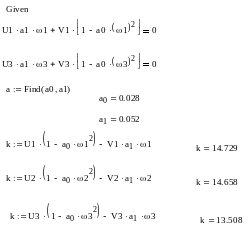
Для построения амплитудно-фазовой частотной характеристики (см. рис. 8.12) в командном окне среды MatLab воспользуемся командой nyquist(sys), а именно

H=tf([15],[0.03 0.03 1])

nyquist(H)

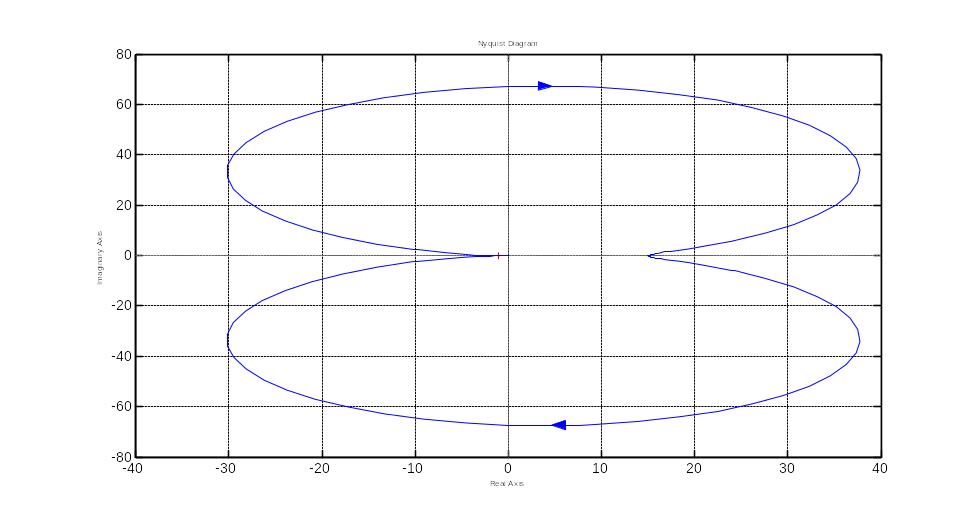
Рисунок 8.12 – Амплитудно-фазовая частотная характеристика математической модели