_Роберт Фишер, Новые методы торговли по Фибоначчи

В данном случае мы не находим в этом отношении асимптотического процесса, потому что деление каждого числа ряда ФИ на его предшествующее значение (например, 4,236-^2,618 или 6,854-Н,236) дает приближенное отношение ФИ = 1,618. Выполнение деления в обратном направлении — а именно деление каждого числа ряда ФИ на следующее значение (например, 2,618^4,236 или 4,236-^6,854) — дает обратное значение константы ФИ, названной нами ранее ФИ' = 0,618. Прежде чем двигатьсядалеепотексту, важно, чтобычитателидоконцапоняли, как получен ряд ФИ из основного ряда суммирования Фибоначчи.

Мы открыли для себя ряд простых чисел, введенных в науку Фибоначчи. Теперь сделаем еще одно краткое отступление прежде, чем использовать ряд суммирования Фибоначчи как основу для разработки торговых инструментов. Сначала рассмотрим, какое отношение имеет ряд суммирования Фибоначчи для окружающей нас природы. После этого останется сделать лишь маленький шаг к выводам, прямо приведущих нас к уместности приложения ряда суммирования Фибоначчи к движению любых международных рынков: валютных или фьючерсных, фондовых или производных.

Мы учитываем уменьшенность колебаний частных вокруг значения 1,618 (или 0,618 соответственно) в ряду Фибоначчи с помощьюболеевысокихилинизкихчисел вволновомпринципе Эллиота, названном Ральфом Нельсоном Эллиотом правилом чередования. И мы представляем инструменты торговли, разработанные нами для самого полного использования магии ФИ. Люди подсознательно ищут божественную пропорцию. Это лишь постоянная и бесконечная борьба за созданиеболеевысокогоуровняжизни.

ОТНОШЕНИЯФИБОНАЧЧИ

Мы — надеемся, и наши читатели — не перестаем удивляться, сколько постоянных значений можно рассчитать с использованием последовательности Фибоначчи, и тому, как отдельные числа, формирующиепоследовательность, повторяютсявстольмногихвариациях. Однаконивкоемслучае нельзя забывать, это не просто игра чисел; это самое важное из когда-либо открытых математических представлений природных явлений. Следующие иллюстрации продемонстрируют некоторые интересныеприложенияэтойматематическойпоследовательности.

Мы подразделили наши наблюдения на два раздела. Сначала кратко пройдемся по отношению Фибоначчи и его присутствию в природных явлениях и архитектуре. Затем кратко опишем, как используютотношениеФибоначчивматематике, физикеиастрономии.

ОтношенияФибоначчивприроде

Чтобы оценить огромную роль отношения Фибоначчи как природной константы, достаточно лишь взглянуть на красоту окружающейнасприроды. Рострастенийвприроде— идеальныйпример общей уместности отношения Фибоначчи и базового ряда суммирования Фибоначчи. Числа Фибоначчиможнонайтивколичестве ответвлений на стебле каждого растущего растения и в числе лепестков.

Можно легко увидеть элементные числа ряда суммирования Фибоначчи в жизни растений (так называемые золотые числа), если пересчитаем лепестки некоторых наиболее распространенных цветов — например, ириса с его 3 лепестками, первоцвета с 5 лепестками, крестовника с 13 лепестками, маргариткис34 лепестками и астры с 55 (и 89) лепестками. Мы должныспросить: случайналиэтамодель(фигура) илимыидентифицировалиопределенныйзаконприроды?

Идеальный пример можно найти в стеблях и цветах тысячелистника (рисунок 1.1). Каждая новая ветвь тысячелистника растет из пазухи, и от новой ветви растут новые ветви. Складывая старые и новыеветви, можнонайтичислоФибоначчивкаждойгоризонтальнойплоскости.

Рисунок1.1 ЧислаФибоначчивцветкахтысячелистника.

При анализе мировых рынков и разработке стратегий торговли мы ищем структуры или фигуры графиков, прибыльные в прошлом (согласно историческим данным). Следовательно, они должны иметь вероятность дальнейшего успеха в будущем. Мы полагаем, что нашли такую структуруилиобщуюфигурувотношенииФибоначчиФИ.

ОтношениеФибоначчиФИиррациональноечисло. Мыникогданебудемзнатьеготочноезначение до последнего знака. Поскольку величина погрешности при округлении отношения Фибоначчи ФИ становитсяменьшепомереростарядасуммированияФибоначчи, мырассматриваем8 каксамоемалое из всех чисел ряда суммирования Фибоначчи, которое может быть с толком использовано для рыночногоанализа(возьмите, кпримеру, частныезначения13-г8 = 1,625 и21-НЗ= 1,615 всравнениис ФИ= 1,618).

В разное время и на различных континентах люди пытались успешно включать в свою работу отношение ФИ как закон точной пропорции. Не только египетские пирамиды построены, согласно отношению Фибоначчи ФИ (более подробное описание см. в книге "Приложения и стратегии Фибоначчидлятрейдеров"), нототжесамыйфеноменнаходимивмексиканскихпирамидах.

Конечно, можно принять во внимание, что египетские и мексиканские пирамиды построены приблизительно в одной и той же исторической эре людьми общего происхождения. Рисунки 1.2а и 1.2ЬиллюстрируютважностьиспользованияпропорцииФибоначчиФИпристроительствепирамид.

Рисунок 1.2а Использование числа ФИ =1,618 в мексиканской пирамиде.

Источник: Mysteries of the Mexican Pyramid, Peter Thomkins (New York: Harper & Row, 1976), pp. 246, 247. Пе-

репечатаносразрешения.

Рисунок1.2Ь Использование числа ФИ =1,618 в мексиканской пирамиде.

Источник: Mysteries of the Mexican Pyramid, Peter Thomkins (New York: Harper & Row, 1976), pp. 246, 247. Пе-

репечатаносразрешения.

Поперечноесечениепирамиды— этоструктура, сформированнаяввиделестницы. Есть16 ступенейвпервомпролете, 42 ступенивовторомиеще68 ступенейвтретьем. ЭтичисласледующимобразомсвязанысотношениемФибоначчи1,618:

Здесь мы находим (хотя и не с первого взгляда) отношение Фибоначчи ФИ в макроструктуре, знакомой всем нам. Наша задача – перенести этот подход из природы и окружающей среды человека в сферу графиков и рыночного анализа. В нашей рыночной среде следует задаться вопросом, сможем ли мы, и если "да", то где обнаружить ФИ столь же полно и наглядно, как в естественнойжизнирастенийиискусственныхпирамидах.

ОтношенияФибоначчивгеометрии

Существование отношения Фибоначчи ФИ в геометрии очень хорошо известно. Однако подходящийдляинвесторовспособпримененияэтогоотношениякакгеометрическогоинструмента к движению биржевых цен с использованием ФИ-спиралей и ФИ-эллип-сов до настоящего времени не публиковался. Чтобы применять ФИ-спирали и ФИ-эллипсы как аналитические инструменты, требуютсяквалификацияпрограммистаисилакомпьютеров.

Поскольку компьютерные мощности сегодня легко доступны, препятствием является отсутствие не железа, а, скорее, некоторых знаний и соответствующего программного обеспечения.

Полностью готовый к работе пакет программ, прилагаемый к данной книге, позволяет каждому заинтересованному читателю/инвестору прослеживать приводимые примеры и генерироватьподобныесигналывторговлеврежимереальноговремени.

ФИ-спираль и ФИ-эллипс имеют необычные свойства, которыевсоответствиисотношением ФибоначчиФИнаходятсявдвухизмерениях: ценаивремя. Весьмавероятно, чтоинтегрирование ФИ-спирали и ФИ-эллипса намного повысит уровень интерпретации и использования отношения Фибоначчи. ДосихпоротношениеФИФибоначчивосновномиспользовалоськакинструментдля измерениякоррекцийирасширенийценовыхколебаний. Прогнозывремениинтегрировалисьредко, потому что они не представлялись столь же надежными, как анализ цен. Но с включением в геометрический анализ ФИ-спиралейиФИ-эллипсовобечасти — иценовой, ивременнойанализ

— могуткомбинироватьсяправильно.

Чтобы лучше понять, как ФИ Фибоначчи геометрически встраивается в ФИ-спирали и ФИ-эллипсы, начнем с описания золотого сечения линии и прямоугольника и их соответствующихотношенийкФИ.

ГреческийматематикЕвклидМегарский(450—370 гг. дон. э.) — первыйученый, написавшийо золотомсечениии, такимобразом, сосредоточившийсянаанализепрямойлинии(рисунок1.3).

ЛинияАВдлинойL разделенанадваотрезкаточкойС. ПустьдлиныАСиСВбудутравныа и b соответственно. Если С являет ся такой точкой, что частное L-т- а равно частному а -s-b, то С золотоесечениеАВ. ОтношениеL -ьаилиа-^ b называетсязолотымотношением.

Рисунок1.3 Золотоесечение линии. Источник: FAM Research, 2000.

Другими словами, точка С делит линию АВ на два отрезка таким образом, что отношения этих отрезков составляют 1,618 и 0,618; мы легко узнаем эти два числа по нашему анализу ряда суммированияФибоначчи, какФИФибоначчииегообратноезначение ФИ'.

Перемещаясь от одной колыбели науки к другой — из Древней Европы в Древнюю Африку или из Древней Греции в Древний Египет, мы узнаем, что в Великой Пирамиде Гизы прямоугольныйэтажпалатыфараонатакжеиллюстрируетзолотоесечение.

Золотое сечение прямоугольника лучше всего продемонстрировать, начертив квадрат, геометрическую конфигурацию, послужившую фундаментом Пирамиды Гизы. Этот квадрат можно затем преобразовать в золотой прямоугольник, как это схематично показано на рисунке

1.4.

Сторона АВ квадрата ABCD на рисунке 1.4 делится пополам. Чертитсядугакругасцентромв точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление DC в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сейразвпропорцияхзолотогопрямоугольника.

Держа в уме представление отношения Фибоначчи ФИ в одномерной (линия) и двумерной (прямоугольник) геометрии, можно перейти к более сложным геометрическим объектам. Они подведутближекинструментам, которыемыхотимприменятьдляанализа параметров времени и ценыфондовыхифьючерсныхрынков.

Рисунок1.4 Золотоесечениепрямоугольника. Источник: FAM Research, 2000.

Единственнойматематическойкривойследующеймоделиестественногоростаявляетсяспираль, выраженная в таких природных феноменах, какSpira mirabilis илираковинанаутилуса. ФИ-спираль называютсамойкрасивойматематическойкривой. Этоттипспираличастовстречаетсявприроде. Ряд суммирования Фибоначчи и золотое сечение, представленное выше как его геометрический эквивалент, оченьхорошоассоциируютсясэтойзамечательнойкривой.

На рисунке 1.5 показана рентгенограмма раковины камерного наутилуса ("кораблика"). Последовательные камеры наутилуса построены, следуя форме ФИ-спирали. По мере роста раковиныразмеркамерувеличивается, ноихформаостаетсянеизменной.

Для демонстрации геометрии ФИ-спирали лучше всего использовать золотой прямоугольник как основание для геометрического анализа. Это показано схематично на рисунке1.6.

Частное от деления длины на высоту прямоугольника ABCD на рисунке 1.6 можно вычислить. Как мы узнали ранее, оно составляет АВ-г-ВС = ФИ-Н = 1,618. Через точку Е, также называемую золотым сечением АВ, проводится линия EF, перпендикулярная АВ, отрезающая от прямоугольника квадрат AEFD. Остающийся прямоугольник EBCF — золотой прямоугольник. Если отделить квадрат EBGH, то остающаяся фигура HGCF также будет золотым прямоугольником. Этот процесс можно повторять неопределенно долго, пока конечный прямоугольникОнестанетнастолькомаленьким, чтобудетнеотличимотточки.

Конечная точка О называется полюсом равноугольной спирали, которая проходит через золотыесеченияD, Е, G, J итакдалее.

Рисунок1.5 ФИ-спираль, представленнаявраковиненаутилуса.

Источник: The Divine Proportion, H. E. Huntley (New York: Dover, 1970), p. iv.

Перепечатаносразрешения.

D

F

J

С

Рисунок1.6 ГеометрияФИ-спирали. Источник: FAM Research, 2000.

Стороны прямоугольника почти, но не полностью касательные кривой.

Отношение ФИ-спирали кряду Фибоначчи очевидно из рисунка 1.6, потому что ФИ-спираль проходит по диагонали через противоположные углы последовательных квадратов, например, DE, EG, GJ и так далее. Длины сторон этих квадратов формируют ряд Фибоначчи. Если самый маленькийквадратимеетсторонудлинойd, смежныйквадратдолжентакжеиметьсторонудлиной d. Следующийквадратимеетсторонудлиной2d (вдвоедлиннееd), следующий 3d (втрое длиннее d), формируярядId, 2d, 3d, 5d, 8d, 13d... которыйявляетсяхорошоизвестнойпоследовательностью Фибоначчи:1—1—2—3—5—8—3—итакдалеедобесконечности.

Спираль не имеет конечной точки. При бесконечном росте наружу (или внутрь) ее форма остается неизменной. Два сегмента спирали идентичны по форме, но отличаются по размеру точно на коэффициент ФИ. Все спирали, чьи темпы роста являются элементами ряда ФИ 0,618- 1,000-1,618-2,618-4,236-6,854-11,090-и так далее, будут в контексте этой книги называться ФИ-спира-лями.

ФИ-спираль — связующее звено между рядом суммирования Фибоначчи, вытекающим из негоотношениемФибоначчиФИ, иволшебствомприроды, котороемывидимвокругнас.

В дополнение к ФИ-спирали, в природе можно встретить и другиеважныегеометрические кривые. Изнихнаиболеесущественные для цивилизации — горизонт океана, след метеора, парабола водопада, дуга перемещения солнца, полумесяц и, наконец, полет птицы. Многие из этих естественных кривых могут быть геометрическисмоделированысиспользованиемэллипсов.

Эллипс — математическое выражение овала. Каждый эллипс можно точно описать с помощьювсеголишьнесколькиххарактеристик(рисунок1.7).

S,S2 на рисунке 1.7 — длина большой оси эллипса. S3S4 — длина малой оси эллипса. Эллипс теперьопределяетсяуравнением

Для нас представляет интерес (в контексте анализа Фибоначчи) отношение главной и малой осиэллипса, выраженноенаматематическомязыкевследующейформуле

Рисунок 1.7 Геометрия ФИ-эллипса. Источник: FAM Research, 2000.

Эллипс превращается в ФИ-эллипс во всех тех случаях, где отношение большой оси к малой оси эллипса является элементным числом ряда ФИ 0,618-1,000-1,618-2,618-4,236-6,854- и так далее. Круг— специальныйтипФИ-эллипса, вкоторома= Ьиотношениеа-=-Ь= 1.

ФИ-эллипсы предпочтительнее всех других возможных эллипсов (с отношениями главных осей, деленных на малые оси, иными, чем числа ряда ФИ), поскольку эмпирические исследования показали, что люди находят приближения ФИ-эллипсов визуально значительно болееудовлетворительными.

Когда участники исследовательского проекта сталкивались с различными формами эллипсов и их спрашивали об уровне комфорта, пробное эмпирическое исследование дало результаты, показанныевТаблице1.1.

Три наблюдателя из четырех предпочли эллипсы, имеющие оси, чьи отношения равны отношению ФИ-эллипса (1,618) или так близко приближены к ФИ-эллипсу, чтобы были почти отнегонеотличимы.

После этого оптимистического обзора перейдем ко второй главной части нашего теоретического представления основных инструментовФибоначчи.

К каким выводам можно прийти после того, что мы уже рассказали? И какие выводы сделал Эллиот, чтобы интегрировать ряд суммирования Фибоначчи и ФИ Фибоначчи с силами, которые двигаютмеждународныерынки?

Таблица1.1	Предпочтения ФИ-эллипсов
Отношение
Главнаяосьмалаяось a-b	Процентнаядоляпредпочтения
1,000	1,2
1,205	0,6
1,250	8,3
1,333	14,7
1,493	42,4
1,618	16,7
1,754	13,1
2,000	1,6

Источник: The Divine Proportion, H. E. Huntley (New York: Dover, 1970) p. 65.

Перепечатаносразрешения.

ВОЛНОВОЙПРИНЦИПЭЛЛИОТА

Ральф Нельсон Эллиот (1871—1948) начал свою карьеру инженером, а не профессиональным аналитиком рынка. Оправившись от тяжелойболезнив30-хгодах, онпереключилсвойинтерес на анализценакций, сосредоточившисьнаИндексеДоу-Джонса.

После нескольких замечательно успешных прогнозов в 1939 году Эллиот опубликовал ряд крупных статей в журнале "Файнэншл уорлд" (Financial World), в которых впервые показал, что ИндексДоу-Джонсадвижетсявопределенномритме.

Рыночная теория Эллиота основана на следующем факте: каждое явление на нашей планете движется по тому же принципу, что и приливы: за приливом следует отлив, за действием — противодействие. Время не влияет на эту схему, потому что структура рынка в своей полноте остаетсяпостоянной.

В этом разделе кратко рассмотрены и проанализированы концепции Эллиота. Однако важно обсудить его идеи, объясняющие фундаментальные концепции и использованные нами в анализе инструментов Фибоначчи. Не будем погружаться в особые детали; большинство фактов подробно описано в книге "Приложения истратегииФибоначчидлятрейдеров".

Наше внимание будет сфокусировано на главных аспектах работы Эллиота, имеющих длительное значение. Даже если мы не соглашаемся с некоторыми открытиями Эллиота, его идеи достойны восхищения. Мы знаем, насколько трудно создавать новые концепциирыночного анализабезтехническойподдержки, доступнойсегодня. КогдамыначалиизучатьработыЭллиотав 1977 году, былооченьтруднодостатьвседанныедляглубокогоанализа. Насколькожетруднееэто должно было быть для Эллиота в те годы, когда он начинал свою работу! Компьютерная технология, доступная сегодня, позволяет быстро тестировать и анализировать, но все же для того, чтобыначать, необходимоиметьвсвоемраспоряженииидеиЭллиота.

Эллиот писал: "Закон природы охватывает наиболее важный изо всех элементов выбор времени. Закон природы не система или метод игры на рынке, а феномен, похоже, отмечающий прогресс всех видов человеческой деятельности. Его применение в прогнозировании революционно".*

Эллиот опирался в своем открытии на закон природы: "Этот закон, стоящий за рынком, можно увидеть только тогда, когда рынок рассматривается в надлежащем свете и затем анализируется с использованием этого подхода. Проще говоря, фондовый рынок создание человека, следовательно, онотражаетхарактерныеособенностичеловека" (с. 40).

Перспектива предсказывать движение цен с использованием принципов Эллиота побуждает легионы аналитиков трудиться день и ночь. Мы сосредоточимся на самой возможностипредсказанияипопробуемответитьнавопрос, возможнолиэто.

Эллиот выразился очень определенно, когда представлял свою концепцию волн: "Любая человеческая деятельность имеет три отличительные особенности: модель (фигура), время и отношение, ивсеониподчиняютсярядусуммированияФибоначчи" (с. 48).

После того, как волны интерпретированы, это знание может применяться к любому движению, потому что одни и те же правила применяются к ценам акций, облигаций, зерновых и других фьючерсов.

Наиболее важный из трех этих упомянутых факторов — модель (ценовая фигура). Модель всегдаразвивается, формируясьвновьивновь. Обычно, хотяиневсегда, можнозаранееувидеть соответствующий тип модели. Эллиот описывает этот рыночный цикл как "...разделенный, прежде всегона'бычийрынок' и'медвежий рынок'" (с. 48).

•The Complete Writings of R. N. Elliott with Practical Application from J. R. Hill, by J. R. Hill, Commodity Research Institute, NC, 1979 (последующихссылкитакжесделанынаЭллиота), р. 84.

Бычий рынок может быть разделен на пять "главных волн", а медвежий рынок — на три главные волны. Главные волны 1, 3 и 5 бычьего рынка подразделены на пять "средних волн" каждая. Затем волны1, 3 и 5 каждой средней волны подразделены на пять "малыхволн"

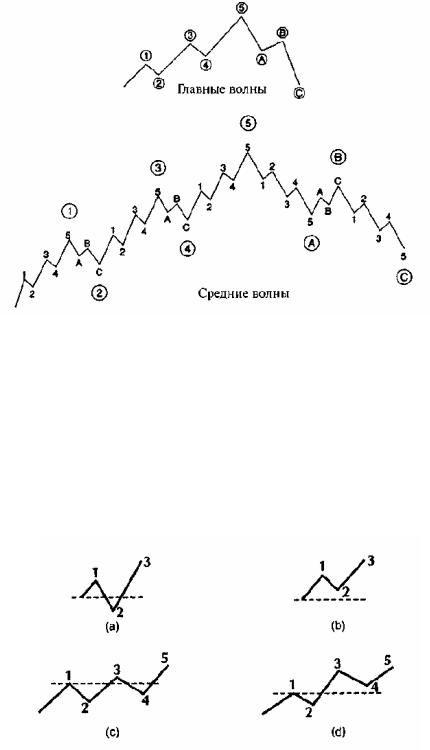
Рисунок 1.8 "Идеальный" цикл фондового рынка по Эллиоту. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 13. Перепечатано с разрешения

Беда с этой общей рыночной концепцией в том, что в большинстве случаев регулярных (правильных) колебанийс5 волнаминебывает. Регулярноеколебаниес5 волнамилишьисключениеиз правила, котороеЭллиотпыталсядовестидоумавведениемвконцепциюсложныхвариаций.

Эллиот представил ряд рыночных моделей (фигур), применимых почти к каждой ситуации рыночногоразвития. Еслиритмрынкаправильный, волна2 небудетвосстанавливаться(retrace) до началаволны1, аволна4 небудеткорректироваться(correct) нижевершиныволны1 (рисунок1.9). Втехслучаях, когдатакоепроисходит, следуетпересчитатьволны.

Рисунок 1.9 Подсчет (а) ошибочен в восходящем движении с 3 волнами; (Ь) правилен в восходящем движении с 3 волнами; (с) ошибочен в восходящем движении с 5 волнами; (d) правилен в восходящем движении с 5 волнами. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 14. Перепечатано с разрешения.