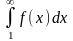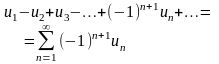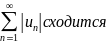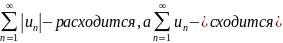- •13.Ряды
- •13.1. Числовые ряды Основные понятия числового ряда
- •Геометрическая прогрессия
- •Свойства сходящихся рядов
- •Знакоположительные ряды Достаточные признаки сходимости
- •Знакочередующиеся ряды
- •Знакопеременные ряды. Абсолютная сходимость. Остаток ряда и его оценка.
- •Исследования знакочередующегося ряда на абсолютную (условную) сходимость.
Исследования знакочередующегося ряда на абсолютную (условную) сходимость.







ряд знакочередующийся
Составим ряд и исследуем его по признакам
сходимости знакопложительных рядов
(необходимый,сравнения, Коши, Даламбера)
нет
да
ответ
Ряд исследуем по признаку
Лейбница
Ряд сходится?
Ряд сходится
да
нет
ряд сходится абсолютно
ряд сходится
условно
ряд расходится
Сводная таблица основных понятий и формул по теме «Числовые ряды»
Ряд |
Сходимость |
Знакопостоянный
u1+u2+u3+¼+un+¼= =
|
ничего о сходимости ряда сказать нельзя, надо применять достаточные признаки. |
2.Признак сравнения. Даны ряды
а). сх ← сх расх → расх б). оба ряда сходятся и расходятся одновременно. |
|
а) при q < 1 ряд сходится; б) при q > 1 ряд расходится; в) при q = 1 признак не работает.
|
|
а) при q < 1 ряд сходится; б) при q > 1 ряд расходится; в) при q = 1 признак не работает. |
|
Если несобственный интеграл
сходится, то и ряд сходится, а если интеграл расходится, то и ряд расходится. |
|
Геометрическая прогрессия
|
|
Ряд Дирихле
|
|
Знакочередующийся
|
Признак Лейбница. Если абсолютные величины членов знакочередующегося ряда удовлетворяют условиям: 1) un>un+1, 2) , то ряд сходится, его сумма положительна и не превсходит первого члена.
|
Знакопеременный
|
Достаточный признак 1)Сходится абсолютно, если
2)Сходится условно, если
( например, по теореме Лейбница). |
ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАЧ
Тема «Знакопостоянные ряды»
В примерах 1 -13 исследовать ряды на сходимость.
Пример 1.
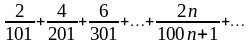
Решение. Воспользуемся необходимым признаком.
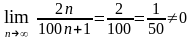 ,
значит, ряд
расходится.
,
значит, ряд
расходится.
Пример
2.
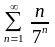 .
.
Решение.
Ясно, что
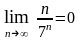 ,
т. е. необходимый признак сходимости
выполняется. Применим признак Даламбера:
,
т. е. необходимый признак сходимости
выполняется. Применим признак Даламбера:
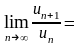
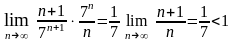 ,
,
значит данный ряд сходится.
Пример
3. Дан ряд
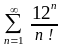 .
.
Решение. Воспользуемся признаком Даламбера
 ,
ряд сходится.
,
ряд сходится.
Пример
4.
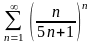 .
.
Решение. Воспользуемся радикальным признаком Коши
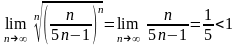 ,
ряд сходится.
,
ряд сходится.
Пример
5.
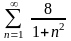 .
.
Решение. Применим интегральный признак Коши. Заменим n на x и вычислим:
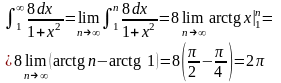
Следовательно, ряд сходится.
Пример
6.
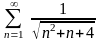 .
.
Решение.
Очевидно, что
 ,
следовательно
,
следовательно
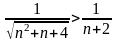 ,
а так как ряд
,
а так как ряд
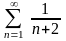 расходится, то и данный ряд расходится.
расходится, то и данный ряд расходится.
Пример
7.
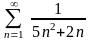 .
.
Решение. Сравним
его с рядом
 ,
который сходится (ряд Дирихле).
,
который сходится (ряд Дирихле).
Воспользуемся замечанием ( формула (13.1.9) и найдём предел отношения:

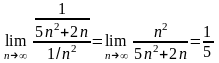 ,
,
значит данный ряд также сходится.
Пример 8.
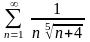 .
.
Решение. Необходимый признак сходимости выполняется, так как
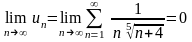 .
.
Следовательно
исследование необходимо продолжить
далее. Воспользуемся достаточным
признаком сравнения. Выберем мажоранту
ряд Дирихле
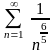 ,
который сходится так как
,
который сходится так как

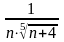 <
<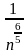
сход ← сход
Пример 9.
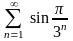 .
.
Решение. Необходимый признак сходимости выполняется, так как
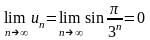 .
.
Сравним с рядом
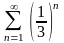 – который представляет собой геометрическую
прогрессию со знаменателем
– который представляет собой геометрическую
прогрессию со знаменателем
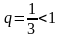 и, следовательно, сходится
и, следовательно, сходится

сход ← сход
Пример
10.
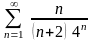 .
.
Решение. По признаку Даламбера
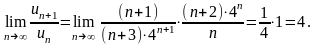
Пример 11.
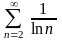 .
.
Решение. Необходимый признак сходимости выполняется так как
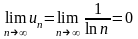 .
.
Далее воспользуемся признаком сравнения
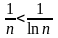 .
.
расход → расход
Пример 12.
1) Какой вывод можно сделать (запишите ответы в пустом эллипсе)
а)

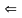
о поведении an
при

б)
о сходимости ряда.
Ответ:
а)
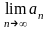 может равняться нулю, а может и не
равняться нулю.
может равняться нулю, а может и не
равняться нулю.
б) ряд с общим членом an может сходиться, а может расходиться.
2 )
Укажите стрелкой, что из чего следует:
)
Укажите стрелкой, что из чего следует:
а)
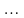
б)
Ответ: а) ←; б) →.
Тема «Знакопеременные ряды»
В примерах 15 – 17 исследовать ряды на абсолютную ( условную ) сходимость.
Пример
13.
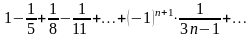
Решение. Проверим условия теоремы Лейбница:
1)
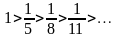 ;
;
2)
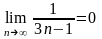 .
.
Оба условия теоремы Лейбница выполнены, значит данный ряд сходится.
Ряд,
составленный из абсолютных величин его
членов расходится: ряд
 ведет себя как гармонический, что можно
установить, воспользовавшись признаком
сравнения. Значит, знакочередующийся
ряд
ведет себя как гармонический, что можно
установить, воспользовавшись признаком
сравнения. Значит, знакочередующийся
ряд
 сходится условно.
сходится условно.
Пример
14.
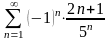 .
.
Решение. Этот ряд сходится по теореме Лейбница. Действительно,
1)
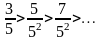 ;
;
2)
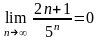 .
.
Ряд
из абсолютных величин данного ряда
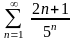 исследуем по признаку Даламбера:
исследуем по признаку Даламбера:
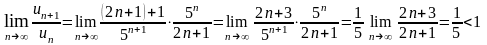 ,
,
значит ряд сходится. Следовательно, данный знакочередующийся ряд сходится абсолютно.
Пример
15.
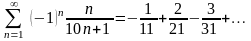 .
.
Решение.
Т. к. второе условие теоремы Лейбница
не выполняется, т.е.
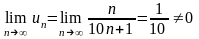 ,
то ряд расходится.
,
то ряд расходится.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
1.Написать простейшую формулу п- го и (п + 1) –го членов ряда по указанным первым членам:
а)
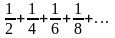 ;
б) 1 +
;
б) 1 +
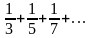 ;
;
в)
1 +
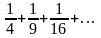 ;
г)
;
г)
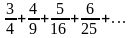 ;
;
д)
7)
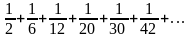 ;
ж) 9) 1 – 1 + 1 – 1 + 1 - …
;
ж) 9) 1 – 1 + 1 – 1 + 1 - …
2. Написать 4 первых члена ряда по известному общему члену:
а)
 ;
б)
;
б)
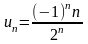 ;
в)
;
в)
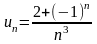 .
.
3.Исследовать знакопостоянные ряды на сходимость:
а)
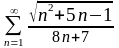 ;б)
;б)
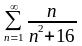 ;в)
;в)
 ;г)
;г)
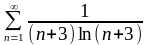 ;
;
д)
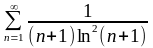 ;
е)
;
е)
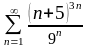 ;
ж)
;
ж)
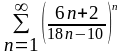 .
.
Ответы. а,б,в,г,е – расходятся; д,ж – сходятся.
4. Исследовать знакочередующиеся ряды на абсолютную, условную сходимость:
а)
 ;
б)
;
б)
 ;
в)
;
в)
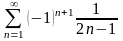 ;
;
г)
 ;
д)
;
д)
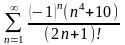 ;
е)
;
е)
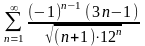 .
.
Ответы. а,г,д,е – абсолютно сходятся, в – сходится условно, б – расходится.

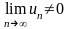
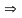 ряд расходится
ряд расходится