7.1. Решето эратосфена

В предыдущей главе отмечалось, что алгоритм представляет собой конечное множество правил для чисто механического решения задач. Первым примером алгоритма в теории чисел будет древний метод нахождения простых чисел, на­зываемый “решетом Эратосфена”, который представляет собой алгоритм опреде­ления простых чисел, меньших заданного целого числа. Проиллюстрируем этот метод, определяя простые числа в интервале от 1 до 100. Прежде всего перечис­лим целые числа от 1 до 100:

Начиная с 2, которая является первым простым числом, выделим жирным шрифтом все числа, кратные 2. Эта процедура очень проста, так как отмеченным должно быть каждое второе целое число, больше 2.

Следующее простое число равно 3. Продолжая процедуру, отметим все чис­ла, кратные 3. Эта процедура также является простой, так как должно быть отмечено каждое третье целое число, больше 3.

Теперь отмечаем все числа, кратные простому числу 5.

Далее отмечаем все числа, кратные простому числу 7.

Поскольку 7 — наибольшее простое число, квадрат которого меньше или равен 100, по теореме 3.41 продолжать процесс нет необходимости. Числа, большие 1 и не отмеченные жирным шрифтом, представляют собой простые числа, которые не превышают 100.

7.2. Метод выделения множителей ферма

Следущая теорема является основой алгоритма разложения на простые множите­ли, названного методом выделения множителей Ферма. Метод используется для определения того, является ли число простым.

ТЕОРЕМА 7.1. Целое нечетное число n > 1 не является простым тогда и только тогда, когда существуют неотрицательные целые числа р и q такие, что n = p² - q², и при этом р - q > 1.

Очевидно, если n можно представить как разность квадратов двух неотри­цательных целых чисел, скажем, n = p² - q², тогда n = (р - q)(p + q). Поскольку р - q > 1, то также р + q > 1; и n не является простым числом.

Обратно, если n = rs где г ≥ s ≥ 1, тогда n можно представить как ((г + s)/2)² - ((г - s)/2)². Поскольку n нечетное, r и s также являются нечетными и, следовательно, r + s и r - s — четные числа. Положив р = (r+s)/2 и q = (r-s)/2, находим, что р и q — целые неотрицательные числа и р - q = s > 1. При n = 1 положим р = 1, a q = 0.

Применение этого метода состоит в попытке найти целые числа р и q такие, что n = р² - q² или, что эквивалентно, р² = n + q², или q² = р² - n. Если используется первое уравнение, полагаем q = 1.2,... до тех пор, пока n + q² не станет полным квадратом. Если до значения q = (n - 1)/2 полный квадрат не достигнут, рассмотрим ситуацию, когда q = (n - 1)/2, что дает n+q² = ((n+1)/2)² и приводит к разложению n на множители n * 1. Поскольку q имеет вид (r - s)/2, где r и s - делители n, то очевидно, что q не может превысить (n - 1)/2. Следовательно, если до значения q = (n - 1)/2 полный квадрат не достигнут, число n является простым.

При использовании второго уравнения, т.е. q² = р² - n, берем в качестве m наименьшее целое число такое, что m² > n, и последовательно полагаем, р = m, m+1,... до тех пор, пока р²-n не станет полным квадратом. Как и прежде, q не может превысить (n - 1)/2, так что если до значения р = (n + 1)/2 полный квадрат не получен, число n является простым. Преимущество использования второго соотношения состоит в том, что проверке на полный квадрат подлежит меньшее количество чисел.

Например, рассмотрим применение записи р² = n+q² для проверки, является ли простым число n = 527. Рассмотрим q = 1,2,..., (n — 1)/2.

Итак, n = 527 является составным, и его делители легко вычисляются:

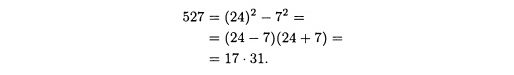
Решение вопроса о том, является ли число п простым, не всегда требует проверки всех значений q от 1 до (п - 1)/2.