Розділ 6. Інтегральне числення функцій багатьох змінних

1. 1. Об'єм циліндричного тіла

Розглянемо в просторі тіло , обмежене зверху поверхнею, заданою рівнянням , збоку – циліндричною поверхнею з твірними, паралельними вісі , знизу областю площини ( – проекція поверхні на площину ). Тіло будемо називати циліндричним з основою (рис. 6.1).

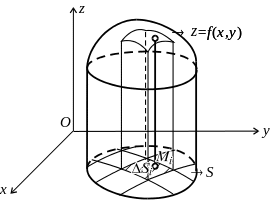
Рис. 6.1.

Для розв'язання поставленої задачі розіб'ємо довільно область на частин: , , ..., і розглянемо циліндричне тіло як сукупність циліндричних стовпчиків з основами , , ..., .

Для визначення об'єму кожного циліндричного стовпчика візьмемо в області довільну точку і побудуємо циліндр із основою і висотою . Такий циліндр обмежений зверху частиною поверхні, рівняння якої . Об'єм цього циліндра можна прийняти за наближене значення об'єму циліндричного стовпчика :

.

Виконуючи обчислення для кожної області ділення і додаючи результати, одержуємо наближене значення об'єму даного циліндричного тіла

.

Отже, отримали об'єм східчастого тіла з основою S, “покритого” зверху частинами площин, рівняння яких

.

Точне значення об'єму циліндричного тіла дорівнює границі, до якої прямує знайдене наближене значення об'єму при необмеженому зменшенні областей ділення, тобто

.

2. 2. Означення подвійного інтеграла

Нехай задана функція , неперервна в деякій плоскій області . розіб'ємо довільно область на частин: , , ..., У кожній замкнутій області виберемо довільну точку . Обчислимо значення функції в обраних точках . Складемо добуток для кожного розбиття. Додамо всі добутки, одержимо суму , яка буде інтегральною сумою для функції в області . Обчислимо границю інтегральної суми функції, за умови, що найбільший діаметр розбиття прямує до нуля. Якщо за цих умов інтегральна сума має скінченну границю, то цю границю називають подвійним інтегралом від функції по області і позначають символами

або .

Таким чином:

. (6.2)

Функція , для якої існує подвійний інтеграл , називається інтегрованою в області .

Геометричний зміст подвійного інтеграла можна пояснити, скориставшись результатом розв'язку розглянутої задачі (рис. 6.1).

Для невід’ємної неперервної в області функції подвійний інтеграл дорівнює об'ємові циліндричного тіла, обмеженого зверху поверхнею з основою у площині .

Якщо ж підінтегральна функція недодатня неперервна в замкнутій області , то подвійний інтеграл дорівнює узятому зі знаком мінус об'ємові циліндричного тіла, обмеженого зверху областю площини , знизу – поверхнею , збоку – циліндричною поверхнею з твірними, паралельними вісі .

Якщо ж неперервна функція є знакозмінною в області , наприклад, додатньою в області і від'ємною в області (рис. 6.2), то подвійний інтеграл дорівнює алгебраїчній сумі об'ємів циліндричних тіл з основами і . У цю суму об'єми тіл, що лежать над площиною , входять зі знаком плюс, а об'єми тіл, що лежать під площиною , входять зі знаком мінус.

Рис. 6.2.

Зазначені поняття використовуються при обчисленні об'ємів тіл за допомогою подвійних інтегралів.