Топологічний простір

Види топологічних просторів

Топологічний простір. Топологія вивчає властивості геометричних фігур, інваріантні щодо всіх взаємно однозначних і взаємно неперервних відображень. Якщо, наприклад, мова іде про поверхню, реалізовану у вигляді гнучкої і розтяжної плівки, то її взаємно однозначними і взаємно неперервними перетвореннями (відображеннями на себе) будуть її розтяг і стиск без розривів і склеювань.

Фундаментальним поняттям топології є поняття топологічного простору, який вводиться таким чином.

Означення:

Множина R, елементи якої називатимемо точками, називається топологічним простором, якщо в ній задано сімейство Ф = { } її підмножин , які називаються відкритими множинами, і притому так, що виконуються наступні аксіоми.

I. Об'єднання будь-якої кількості (скінченної або нескінченної) відкритих множин є відкрита множина.

II. Перетин будь-яких двох відкритих множин є відкрита множина.

3. Порожня множина 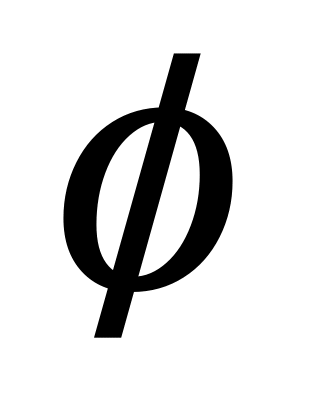і вся множина R є відкритими множинами.

Вважають , що сімейство Ф = { } є топологічною структурою на R, або просто топологією. Таким чином, топологічний простір є пара, яка складається із множини R і введеної на ній топологічної структури Ф. Топологічний простір позначається через (R, Ф) і лише в тих випадках, коли ясно, про яку топологічну структуру Ф йде мова, топологічний простір (R Ф) позначається просто через R.

З аксіоми II слідує, що перетин скінченного числа відкритих множин є відкрита множина.

Розглянемо приклади топологічних просторів.

Приклад I.

У довільній нескінченній множині R відкритими множинами вважатимемо тільки дві множини — порожню множину і саму множину R. Така топологія називається тривіальною.

Приклад 2.

Нехай R — довільна множина. Відкритими множинами вважатимемо всі підмножини множини R, включаючи порожню множину. Така топологія називається дискретною.

Означення:

Околом точки а топологічного простору R називають будь-яку відкриту множину U R, що містить точку а.

Нехай R — топологічний простір, а М — довільна множина точок цього простору. Точка а М називається внутрішньою точкою множини М, якщо існує такий окіл U точки а, що U М. Має місце наступна теорема.

Теорема .

Всі точки відкритої множини є внутрішніми точками. Навпаки, якщо всі точки множини F R топологічного простору (R, Ф) внутрішні, то множина F є відкритою.

Доведення.

Перша частина теореми очевидна, тому доведемо тільки другу частину теореми. Оскільки всі точки множини F внутрішні, то для будь-якої точки а цієї множини існує такий окіл U , що U F. Легко побачити, що F = U_a. Згідно аксіоми І, F — відкрита множина.

Теорема доведена.

Покажемо, що будь-яка підмножина топологічного простору може бути розглянута як топологічний простір. Справді, нехай (R, Ф) топологічний простір, а М підмножина множини R..

Означення:

Відкритою множиною в М назвемо будь-яку її підмножину виду

F' =М F , де F' - будь-який елемент сімейства Ф. Легко переконатися в тому, що при цьому визначенні виконуються всі аксіоми I- III топологічного простору, тому ми говоритимемо, що на множині М індукується (породжується) топологічна структура Ф' = { F' }.

Топологічний простір (М,Ф') називається підпростором топологічного простору (R, Ф)

Метричні простори.

Важливим класом просторів, в яких легко може бути задана топологія, є метричні простори (R, ).

Покажемо, що метричні простори є окремим випадком топологічних просторів; точніше, покажемо, що задання метрики в множині R дозволяє природним чином визначити топологічну структуру в просторі (R, ). Для цього достатньо в (R, ) ввести поняття відкритої множини так, щоб були виконані аксіоми I-III.

Означення:

Кульовим r-околом точки а простору (R, ) назвемо множину всіх точок простору (R, ), що задовольняють умову (позначення: U(а,r)).

Означення:

Відкритою множиною простору (R, ) назвемо або порожню множину, або будь-яку непорожню множину М , що задовольняє умову: для кожної точки а M існує хоч би один кульовий окіл точки а, що цілком

належить множині М. Визначена таким чином топологія Ф називається топологією, що індукується в (R, ) метрикою або просто топологією метричного простору (R, ).

З наведеного визначення слідує, що в топологічному просторі (М, ) порожня множина і сімейство куль {U (а, r )}, де а пробігає все R, а r — всю сукупність додатних чисел, утворює базис простору.

Розглянемо приклади.

Приклад .

У метричному просторі (R, ) будь-який кульовий — r -окіл U ( а, r) є відкритою множиною. Відкритими множинами будуть також перетини кінцевої безлічі кульових околів і об'єднання будь-якої скінченної або нескінченної множини кульових околів.

Приклад .

В евклідовому арифметичному просторі Е₁ інтервал (а,в) є відкритою множиною, а сегмент [а, в] не є відкритим множиною.

Останнє твердження виходить з тієї обставини, що будь-який r — окіл точки а (або в) містить точки, що не належать сегменту [а, в] .

Введемо поняття підпростору метричного простору (R, ). Для цього відмітимо, що будь-яка множина М метричного простору (R, ) сама є метричним простором (М, ), тому метрикою на (М, ) індукується топологічна структура Ф . Таким чином, розглядаючи простори (R, ) і (М, ) як топологічні простори, можна вважати, що (М, ) є підпростором простору (R, ).

Аксіома відокремлення.

Топологічний простір називається хаусдорфовим, якщо виконується наступна аксіома:

Для будь-яких 2х різних точок простору R існують околи, які містять ці точки не перетинаються.

Наприклад, хаусдорфовим є метричний простір. Дійсно, нехай а і b різні точки, а . Кола і очевидно не перетинаються – не мають спільних точок.

Підпростір хаусдорфового простору є хаусдорфовим простором.

Зв’язність.

Топологічний простір R називається незв’язним, якщо існує 2 не порожні множини M і N таких, що M N= і M N=R. Простір R називається зв’язним, якщо він не є незв’язним.

Не порожня відкрита зв’язна множина М R називається областю.

1. Властивість топологічного простору бути зв’язним є топологічним інваріантом.

2. Властивість множини Х топологічного простору бути зв’язною є топологічним інваріантом.

Теорема.

Сегмент є зв’язним топологічним простором.

Доведення. (від супротивного)

Припустимо, що існують відкриті множини U і V, які задовольняють умовам U V=І, U V= .

Розглянемо скалярну функцію скалярного аргументу f: , яка визначається так: f(x)=1, якщо х U і f(x)=-1, якщо х V. Функція f(x) неперервна на І функція. Справді, нехай х₀ будь-яка точка відрізка, припустимо, що х₀ U. Так як U область, то за означенням існує окіл (кругова область) , що цілком належить множині U. Звідси слідує, що у всіх точках інтервалу значення функції дорівнює 1, тобто функція неперервна в точці х₀. Ми дійшли до суперечності з теоремою Коші про проміжне значення.

Простою дугою називають гомеоморфний образ сегменту.

3. Проста дуга є зв’язним топологічним простором.

Топологічний простір, будь-які 2 точки якого можна з’єднати простою дугою називається лінійно зв’язним.

4. Лінійно зв’язний топологічний простір (множина топологічних просторів) є зв’язним.

Доведення. (від супротивного)

R – лінійно зв’язний топологічний простір, для якого існують не порожні множини M і N, які задовольняють умовам M N=R і M N= . Нехай a M, b N, а L – проста дуга, яка з’єднує ці 2 точки. В силу співвідношень L M N, L M = , L N= , і M N L= , множина L незв’язна, що суперечить властивості 3.

5. Кругове кільце не гомеоморфне кругу Q.

Кругове кільце S є множиною точок евклідової площини ТЕ₂, які розміщені між двома концентричними колами С₁ і С₂. Точки, які лежать на С₁ чи на С₂ до S не належать. Кола С₁ і С₂ разом утворюють межу множини S.

Щоб встановити, що множини Q і S не гомеоморфні, міркуємо так: якщо ми з’єднаємо відрізком дві точки, які належать відповідно колам С₁ і С₂ і лежать на одному і тому ж радіусі, і виключимо з S всі точки цього відрізка, то за властивістю 4 множина залишиться зв’язною. Якщо ж ми в Q з’єднаємо відрізком дві будь-які точки його межі С, то після виключення з Q всіх точок цього відрізка множина розпадеться на дві компоненти. Оскільки зв’язність є топологічним інваріантом, то звідси слідує, що множини Q і S не гомеоморфні.

Компактність.

Відкритим покриттям топологічного простору (R, Ф) називається сукупність множин , якщо .

Топологічний простір R називають компактним, якщо із всякого його відкритого покриття можна виділити кінцеве відкрите покриття.

Відкритим покриттям множини М топологічного простру R називається сукупність відкритих множин простору R, якщо М .

Для того, щоб М була компактною множиною, необхідно і достатньо, щоб з будь-якого відкритого покриття множини М в R можна було виділити кінцеве покриття.

Для E_n необхідною і достатньою умовою компактності множини є її замкнутість і обмеженість.

Властивість топологічного простору бути компактним є топологічним інваріантом.