10. Приведение задач к канонической форме. Табличная реализация симплекс-метода.

11. Двойственная задача. Взаимодвойственность.

В силу всеобщности рассмотрим каноническую задачу в виде:

(1)

все выводы справедливы в силу теоремы 4 для произвольной линейной задачи. По параметрам задачи (1) построим некоторую другую линейную задачу:

(2)

Предположим, что у задачи (1) существует – оптимальный базисный план. Построим вектор (3)

Вектор называется вектором потенциалов для плана . Докажем, что он является оптимальным планом задачи (2).

Доказательство. Из (3) вытекает, что и протранспонировав, получим (4)

В силу оптимальности выполняется условие или , или . Протранспонировав, получим:

(5)

Объединяем (4) и (5):

Сравнивая это соотношение с ограничениями задачи (2) видим, что они выполняются (только 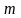из них принимает вид равенств). Подсчитаем на векторе значение целевой функции задачи (2):

(6)

Возьмём произвольный план задачи (2): 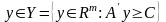и оценим на нём значение целевой функции:

(7)

Из (7) видно, что на произвольном плане задачи (2) целевая функция ограничена снизу числом , а на плане эта нижняя граница достигается (6), следовательно, вектор .

Вывод: если – оптимальный план задачи (1), то соответствующий ему вектор потенциалов – оптимальный план задачи (2).

Ч.т.д.

Задача (2) называется двойственной к задаче (1), а вектора 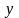– двойственными планами. Задачи (1) и (2) тесно связаны между собой.

12. Соотношения двойственности 1,2.

Соотношение 1 (основное неравенство). Пусть – множество прямых планов, – множество двойственных планов. Для любого справедливо неравенство:

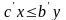(10)

Доказательство. Возьмём произвольную пару и умножим основные ограничения задачи (1) слева на , а основные ограничения задачи (2) слева на имеем (учитывая, что ):

, .

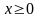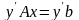Вычитая из неравенства равенство, получим:

Таким образом,

Ч.т.д.

Соотношение 2 (теорема двойственности). Для существования оптимального плана прямой задачи необходимо и достаточно существование оптимального плана двойственной задачи, причём оптимальные значения целевой функции одинаковы:

(11)

Доказательство. Достаточность. Пусть оптимальный план задачи (1). Можно считать, не ограничивая общности, его оптимальным базисным планом (выводы двухфазного метода), тогда оптимальный план задачи (2).

Необходимость. Пусть существует оптимальный план задачи (2). Считая эту задачу прямой и используя достаточность, можно сделать вывод, что у прямой задачи существует оптимальный план.

Ч.т.д.