Лабораторная работа №5

Тема «Симплекс-метод»

Цель. Научиться решать ЗЛП симплекс-методом

Задачи. Решить свой вариант двумя способами

- «вручную» используя основные(неосновные) переменные

- через симплекс-таблицу

Задание для решения

Предприятие производит 3 вида продукции: А1, А2, А3, используя сырье двух видов: В1 и В2. Известны затраты сырья i-го вида на единицу изделия j-го вида а_ij , количество сырья каждого вида b_i (i = 1, 2), а также прибыль, полученная от единицы изделия j-го вида с_j (j = 1, 2, 3).

Сколько изделий каждого вида необходимо произвести, чтобы получить

1) максимум прибыли;

2) максимум товарной продукции?

Обозначения:

в таблице приведена матрица затрат: А = (а_ij),

справа от таблицы значение b_i (i = 1, 2)

и внизу с_j (j = 1, 2, 3).

Варианты заданий

Контрольные вопросы

1. Дайте определение симплекс-разности.

2. Сформулируйте критерий оптимальности в алгоритме симплекс-метода.

3. Сформулируйте критерий отсутствия решений в алгоритме симплекс-метода.

4. Сформулируйте основные моменты, которые должен содержать любой конечный

5. алгоритм решения ЗЛП.

6. Какие ЗЛП не могут быть решены симплекс-методом?

7. Из чего состоит отчет по результатам поиска решения MS Excel?

8. Из чего состоит отчет по устойчивости поиска решения MS Excel?

9. Из чего состоит отчет по пределам поиска решения MS Excel?

Лабораторная работа №6

Тема «Анализ решения задач ЛП на основе отчетов MS Excel»

Цель: Научиться исследовать решение задач ЛП на основе отчетов MS Excel

Задачи:

Изучить теоретический материал по теме «Теория двойственности в линейном программировании»

об использовании отчетов MS Excel

Закончить самостоятельную работу (21.02.2012)

Решить ЗЛП симплекс-методом:

Оформить решение в виде отчета

Лабораторная работа №7

Тема «Использование средств MS Excel для решения задач линейного программирования»

Цель: Изучение способа решения задач линейного программирования с помощью MS Excel и проверка результатов, полученных ранее с помощью графического метода.

Задачи:

• Изучить теоретический материал об использовании средств MS Excel

• Решить ЗЛП из лаб.работы №4 (свой вариант) в MS Excel, используя надстройку «Поиск решения»

• Сравнить результаты, полученные ранее при решении с помощью графического метода, с результатами, полученными программой.

Выполнить задание №1.

Выполнить задание №2.

Лабораторная работа 8

Тема «Транспортная задача. Задача о назначениях»

Цель: Изучение моделей линейного программирования: транспортной задачи и ее частного случая задачи о назначениях. Изучение способа решения данных задач средствами MS Excel.

Задачи:

• Изучить теоретический материал о транспортной задаче и задаче о назначениях.

• Изучить теоретический материал о решении транспортной задачи и задач о назначениях в среде MS Excel.

• Решение практических задач в среде MS Excel.

• Исследовать результаты и составить отчет.

Предоставить

- задачи, рассмотренные на семинаре, а также

Решить:

Задача№1

Пусть имеются 4 поставщика S и 5 потребителей D. Издержки перевозки единицы груза от i-го поставщика в j-й пункт назначения, запасы поставщиков и заказа потребителей даны в таблице. Оптимизировать план перевозок.

	D1	D2	D3	D4	D5
S1	13	7	14	7	5
S2	11	8	12	6	8
S3	6	10	10	8	11
S4	14	8	10	10	15

Организуйте данные так, как показано ниже на рис.1.

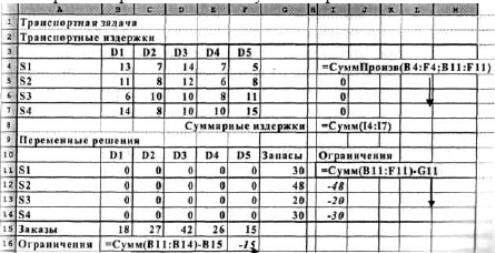
Рис.1 Транспортная задача

1. В ячейках I4-I7 - суммы произведений цены перевозки единицы груза на объем перевозки от i-го поставщика к любому потребителю. В ячейке 18 сумма этих сумм (т.е. двойная сумма) - целевая функция, которую нужно минимизировать.

a) В ячейках I11:I14 — ограничения на количества груза, которые нужно увезти от каждого поставщика.

b) В ячейках B16:F16 - ограничения на количества груза, которые нужно привезти к каждому потребителю.

2. Вызовите "Поиск решения":

a) Целевая ячейка: I8, - Мин

b) Изменяя ячейки: B11:F14

c) Ограничения: B11:F14 ≥ 0 (перевозки неотрицательны)

I11:I14 = 0 (ограничения на количества груза от каждого поставщика)

B16:F16 = 0 (ограничения на количества груза каждому потребителю)

При такой организации данных все перевозки окажутся целыми числами (если целыми являются числа в колонках "Запасы" и строке "Заказы").

Однако не следует требовать явно, чтобы переменные В11-F14 были целыми!

3. Проверьте, что в полученном решении ровно т + п - 1 ненулевых перевозок.

4. Повторите расчет, максимизируя транспортные издержки, чтобы оценить отличие наилучшего варианта от наихудшего.

Задача №2

Фирма, занимающаяся продажей оборудования для компьютерных сетей, имеет 10 специалистов по маркетингу и 10 техников-программистов, которых необходимо объединить в пары (техник - менеджер по маркетингу) - команды по продаже оборудования, соответствующего нуждам конкретного клиента. Менеджер по работе с персоналом провел среди них тест Майера-Бриггса и определил индекс взаимной несовместимости между i-м техником и j-м маркетологом. Индекс варьирует от 20 (выраженная враждебность) до 1 (дружеские отношения). Результаты представлены в таблице индексов несовместимости. Составить команды так, чтобы суммарный индекс был минимальным.

Индексы несовместимости

Менеджер по маркетингу	Техники
	Ваня	Петя	Миша	Коля	Вася	Рома	Майя	Витя	Инна	Гена
Аня	11	8	15	3	9	17	14	6	12	2
Зоя	7	4	13	11	19	2	10	5	18	9
Маша	13	20	19	12	14	11	16	9	15	14
Виталий	5	8	12	6	1	3	4	7	10	12
Люба	16	7	18	9	13	1	2	17	12	3
Даша	12	3	11	17	5	6	18	2	1	4
Руслан	9	1	20	4	7	20	19	1	19	16
Валя	8	6	17	8	11	4	3	4	13	16
Юля	17	2	19	13	14	19	11	3	17	1
Галя	12	1	20	1	2	5	6	4	1	13

Решение

1. Организуйте данные так, как показано на рис.2 "Построение команд".

Отличие от транспортной задачи только в том, что все "Запасы" и "Заказы" равны единице. Сделав первую таблицу, скопируйте ее на новое место, обнулите все значения переменных решения и добавьте строчки ограничений (из единиц). Формулы для левых частей ограничений такие же, как и в предыдущей задаче.

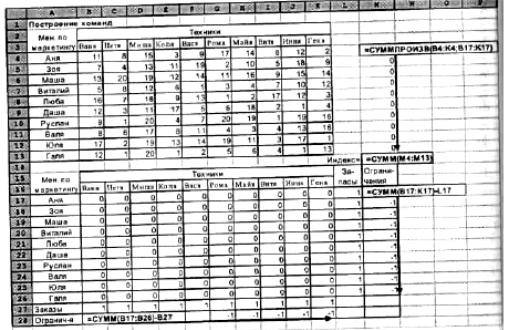
Рис.2 Организация данных в MS Excel «Построение команд»

2. Целевая функция вычисляется как сумма сумм произведений строки с индексами несовместимости и строки переменных решения. Каждая такая сумма произведений это индекс образованной команды. Действительно, в строке переменных все числа равны нулю, кроме одного, которое стоит на пересечении строки с именем маркетолога и столбца с именем техника (см. рис. 3). Это число равно 1, и оно указывает на то, что команда сформирована именно из этих j двух участников. Именно эта единица, будучи умножена на индекс несовместимости участников этой команды, дает значение всей суммы произведений, поскольку остальные произведения в этой сумме - нули.

2. Вызовите "Поиск решения". В отличие от предыдущей задачи все переменные окажутся равными 0 или 1. Однако не следует требовать явно, чтобы они были целыми и меньшими или равными 1!

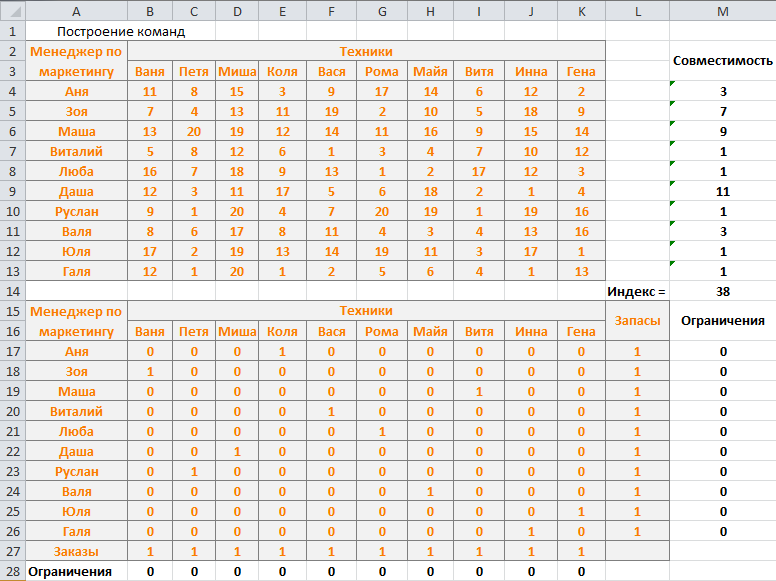
Рис.3. Результаты для примера «Построение команд»

Альтернативные решения Решение задачи, показанное на рис. 3 "вырождено" (различным наборам переменных решения отвечает одно и то же оптимальное значение целевой функции). Цифры над суммарным индексом, дают индексы сформированных команд.

Получить различные наборы этих индексов (соответствующих различным наборам переменных решения) можно повторно запуская "Поиск решения" после нахождения очередного оптимального решения (не обнуляя переменные решения). Особенности алгоритма, используемого MS-Excel, позволяют последовательно получить 3 альтернативных решения без специальных усилий.

Эти решения совершенно одинаковы с точки зрения поставленной оптимизационной задачи. Однако менеджер предпочтет решение, показанное в первом столбце Действительно, при одинаковом суммарном индексе составленных команд - 38 (или среднем индексе 3,8) в этом решении нет совсем уж плохих команд. Наихудший индекс 11 (что можно трактовать как почти нейтральные отношения), в то время как для решений, показанных в первых двух столбцах, есть команды с индексами 13 и 19.

Наличие альтернативных решений полезно для менеджера, поскольку дает возможность выбрать из них наилучшее решение с точки зрения факторов, оставшихся неформализованными. В данном случае неформализованным осталось требование о том, что каждая из команд должна иметь индекс не хуже некоторого заданного числа.

На первый! взгляд нетрудно явно ввести это требование в решение.

Явное ограничение индекса команды

Действительно, просто потребуем, чтобы все числа в ячейках М4-М13 (т.е. индексы образованных команд) были не больше 11. К сожалению, нельзя ограничить их меньшим числом, так как, уникальный техник "Миша" имеет минимальное значение этого индекса, как раз равное 11, и может более или менее уживаться только с маркетологом "Дашей". Таким образом, либо "Мишу" надо уволить, либо согласиться с тем, что наихудшая команда не может иметь индекс меньше 11. Остановимся пока на втором варианте. Решение модифицированной задачи показано на рис. 4 видно, что в нем что-то "катастрофически не так". Переменные решения оказались не целыми. Почему так получилось? Дело в том, что введенное дополнительное ограничение превратило нашу задачу о назначениях (по существу транспортную задачу) в обычную задачу линейного программирования. Для такой задачи специализированные "транспортные" методы решения неприменимы. А как указывалось раньше, только они обеспечивают целочисленные решения без введения явных требований целочисленности. Получившуюся общую ЛП-задачу MS-Excel решают с помощью обычного симплекс-метода, а он отнюдь не гарантирует целочисленности переменных решения. Можно возразить, что целочисленное решение этой ЛП-задачи при добавленном ограничении на индексы команды существует. Соответствующие ему индексы команд изображены на рис. 3 в крайнем справа из трех приведенных столбцов с индексами составленных команд. Почему же "Поиск решения" его не показал? Ответ заключается в том, что сформулированная ЛП-задача тоже вырожденная, т.е. несколько наборов переменных решения соответствует одному и тому же значению целевой функции. Симплекс-метод сводится к одному из решений в зависимости от того, из какой угловой точки области допустимых планов начать процесс поиска. Стандартно этот процесс начинается из начала координат (т.е. все переменные решения первоначально предполагаются равными нулю). В данном случае симплекс-метод выбрал не то решение, которого бы нам хотелось…

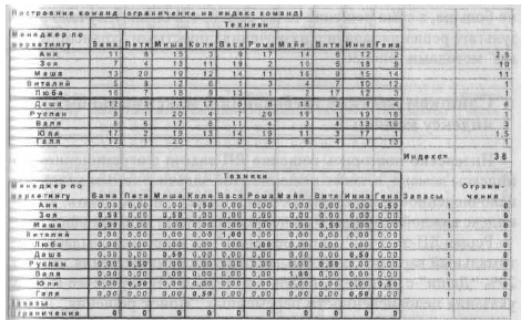
Рис.4. Результаты для примера «Построение команд» при ограничении на индекс команд

Условие целочисленности

Можно, разумеется, явно потребовать, чтобы все переменные решения были целыми. Введем дополнительное ограничение В17:К26- целое. В этом случае процесс решения занимает несколько большее время. "Поиск решения" должен использовать алгоритм целочисленного программирования. Решение находится только после продолжения поиска за установленным по умолчанию пределом допустимых итераций. В середине решения программа выбрасывает окно с вопросом "Достигнуто максимальное число итераций. Продолжить?". Нужно ответить "да". Правда, решение этой гораздо более сложной, чем исходная, задачи тоже занимает всего несколько секунд. Все же заметно, что время решения существенно больше, а само решение то же самое, что было получено в результате решения задачи о назначениях простыми "транспортными" методами.

Слишком жесткие требования к максимальному индексу команд

Интересно повторить решение ЛП-задачи с ограничением на индексы команд, а также решение этой задачи с явным условием целочисленности переменных решения, если потребовать, чтобы индекс каждой команды был не больше 9 (или еще меньше). Решая ЛП-задачу, "Поиск решения", не колеблясь, выдаст "оптимальный вариант" с дробными переменными решения, спарив 20% "Даши" с "Мишей", а 80% - с "Инной". В случае же явного указания целочисленности переменных "Поиск решения" будет решать задачу минут 10, прежде чем ответит, что решения нет.

Мораль

Введение в транспортную задачу или в задачу о назначениях не свойственных им дополнительных ограничений приводит к тому, что эффективные "транспортные" методы решения таких задач (метод "северо-западного угла", циклические перестановки и т.п.) перестают быть применимыми. В этом случае задача будет решаться с помощью общих алгоритмов решения ЛП-задач (например, симплекс-методом). Помимо того что эти методы менее эффективны, они не могут гарантировать целочисленного решения, которое обычно предполагается в транспортной задаче и абсолютно необходимо в задаче о назначениях. Прямое требование целочисленности переводит проблему в разряд моделей целочисленного линейного программирования, которые являются гораздо более трудными для решения и анализа.

Заключение

Постановка транспортной задачи предусматривает задание двух таблиц: таблицы транспортных издержек для перевозок единицы груза c_jj и таблицы объемов перевозок X_ij от i-го поставщика к j-му потребителю. Эти таблицы имеют m строк (по числу поставщиков) и n столбцов (по числу потребителей). Необходимо также задать запасы поставщиков, готовые к вывозу (столбец Si) и величины заказов потребителей (строка Dj).

Транспортная задача обязательно должна обладать свойством сбалансированности: сумма запасов производителей должна быть равна сумме заказов потребителей.

Если это условие в реальности не выполняется, необходимо сбалансировать задачу, а именно:

• если сумма запасов превышает сумму заказов, в таблицы издержек и перевозок нужно ввести лишнюю строку "фиктивного потребителя", который "заказывает" весь реальный избыток запасов поставщиков. При этом транспортные издержки при перевозке запаса от любого реального поставщика к "фиктивному потребителю" должны быть равны нулю. Перевозки, "доставленные" к "фиктивному потребителю" от каждого поставщика, означают, что эти запасы реально остались на складах поставщиков;

• если сумма заказов превышает сумму запасов, в таблицы издержек и перевозок нужно ввести лишний столбец "фиктивного поставщика", который "предлагает" покрыть весь дефицит запасов реальных поставщиков. При этом транспортные издержки при перевозке запаса от "фиктивного поставщика" к любому реальному потребителю должны быть равны нулю. Перевозки, "доставленные" от "фиктивного поставщика" каждому реальному потребителю, означают величину непоставленного запаса этому потребителю.

Сбалансированность и специальная структура ограничений транспортной задачи обусловливают важное свойство оптимального плана перевозок: его следует искать только среди множества опорных планов. Опорным называется такой план, в котором количество ненулевых перевозок равно сумме количеств поставщиков и потребителей минус единица. В связи с этим алгоритм решения транспортной задачи разбивается на две стадии:

• запись какого-нибудь опорного плана;

• переход от одного опорного плана к другому, с меньшими суммарными затратами. И для той и для другой стадии разработаны алгоритмы, гораздо более эффективные, чем обычный симплекс-метод.

Важной особенностью этих алгоритмов является целочисленность оптимального плана перевозок (при условии, что запасы и заказы - целые).

При решении транспортной задачи с помощью MS-Excel "Поиск решения" автоматически выберет специальные эффективные алгоритмы решения и обеспечит целочисленность решения (без специального требования целочисленности!), если организация данных и введенные ограничения соответствуют транспортной задаче.

Задача о назначениях представляет собой частный случай транспортной задачи с числом строк (поставщиков), равным числу столбцов (потребителей). Каждый "поставщик" (это может быть рабочий) предлагает самого себя одному из "потребителей" (это может быть операция, станок или напарник). Поэтому все "запасы" и "заказы" в задаче о назначениях равны 1.

Домашнее задание: Аранович

1. гл.7. Задача из диапазона 7.1-7.5.

Номер задачи = номер студента в списке +5*n

2. гл.8 Задача 8.1-8.2 (четный/нечетный номер в списке)

Лабораторная работа №9

Тема «Матричные игры в чистых стратегиях»

Цель: Изучение и реализация алгоритма нахождения равновесной ситуации в матричной игре с помощью минимаксного метода в чистых стратегиях.

Задачи:

• Изучить теоретический материал о матричных играх в чистых стратегиях.

• Изучить минимаксный метод нахождения равновесной ситуации в матричной игре.

• Разработать алгоритм, реализующий нахождение стратегий двух игроков, приводящих к равновесной ситуации или указывающий об отсутствии равновесной ситуации.

• Реализовать этот алгоритм, для равновесной и неравновесной ситуациям

• Провести моделирование и исследовать результаты

• Подготовить отчет

Вопросы для зачета

1. Дать определение конфликта и охарактеризовать его составляющие

2. Что такое «игра» с точки зрения теории игр.

3. Описать основные понятия теории игр(игра, игроки, стратегия, ситуация, выигрыш)

4. Что такое оптимальное решение в игре, равновесие?

5. Описать основные положения матричной игры, привести пример.

6. Рассмотреть на примере равновесную ситуацию(maxmin, minmax, оптимальная стратегия)

7. Общий алгоритм поиска ситуации равновесия в игре (нижнее/верхнее значение игры, максиминная/минимаксная стратегии)

8. Доказать, что нижнее значение игры всегда ≤ верхнего. Просчитать количество сравнений в платежной матрице в общем алгоритме.

9. Пояснить термины: цена игры, седловая точка, решение матричной игры с седловой точкой. Может ли быть в игре несколько седловых точек?

Лабораторная работа №10

Тема «Матричные игры в смешанных стратегиях»

Цель: Построение решения 2×n и m×2 матричных игр наглядно-графическим методом в смешанных стратегиях

Задачи:

1. Изучить теоретический материал по смешенному расширению матричной игры

2. Изучить наглядно-графический метод решения матричных игр

3. Найти решения игр, предложенных в примерах и

4. Самостоятельно разработать и решить 2×n игру (n=5-7) используя EXCEL для построения графиков

5. Оформить отчет

Х од выполнения

1. Получить формулу среднего выигрыша для смешанного расширения игры «чет-нечет» с матрицей 2×2

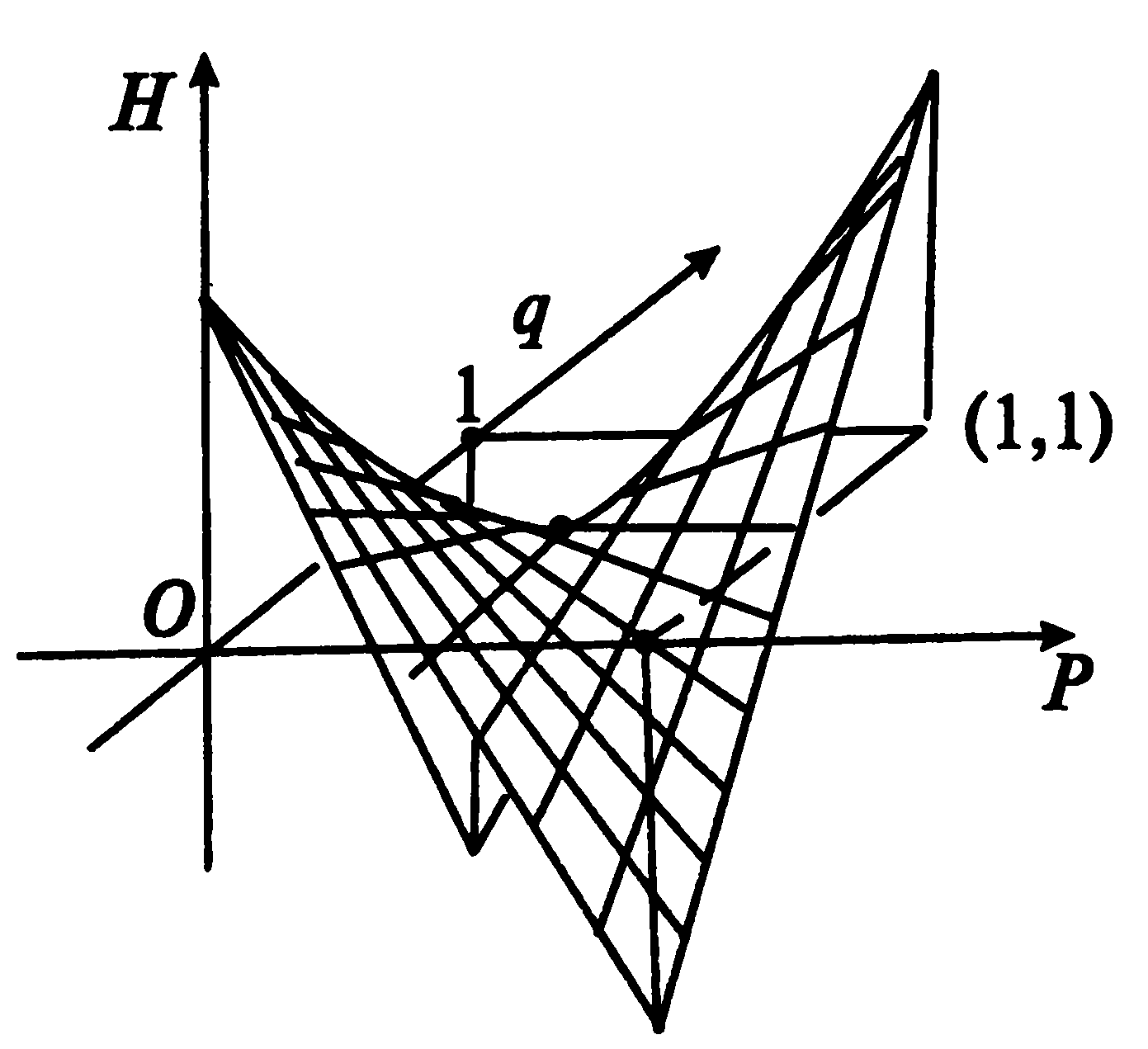
2. Вручную построить график этой функции (гиперболический параболоид),

с седловой точкой

3. Самостоятельно разработать и решить 2×n игру (n=5-7) используя EXCEL для построения графиков. Описать пошагово ход решения, привести графики!!!

Вопросы для зачета

1. При каких условиях переходят к смешанному расширению игры?

2. Определить понятие «смешанная стратегия». Какая связь между чистой и смешанной стратегиями?

3. Как описывается ситуация в смешанных стратегиях, каков средний выигрыш игрока?

4. Рассмотреть смешанное расширение игры «чет-нечет» с 2х2-матрицей

5. Что такое оптимальные смешанные стратегии и как они связаны с равновесной ситуацией? Привести математическую формулировку решения матричной игры в смешанных стратегиях.

6. Сформулировать Основную теорему теории матричных игр (Дж.фон Нейман) : о решении матричной игры в смешанных стратегиях

7. Сформулировать теорему 1 – о роли чистых стратегий при поиске решения матричной игры в смешанных стратегиях

8. Сформулировать теорему 2 – о возможности нахождения min/max мат.ожидания выигрыша игрока в смешанных стратегиях на множестве его чистых стратегий. +Следствие.

9. Сформулировать теорему 3 – о равенстве значения среднего выигрыша игрока для любой положительной вероятности из оптимального набора значению игры. + Следствие.

10. Пояснить положения, лежащие в основе наглядно-графического метода решения матричных игр 2 х n.

11. Описать общую схему решения задачи наглядно-графическим методом матричных игр 2 х n.

12. Показать, как найти полное решение игры (т.е.зная опт.смеш.стратегию игрока А отыскать опт.смеш.стратегию игрока В)

13. Найти решение матричной игры 2 х n (m х 2) наглядно-графическим методом с конкретными значениями платежной матрицы.

Доп.материал(лекционный)

Т.е.

Лабораторная работа №11

Тема «Решение матричных игр методами линейного программирования»

Цель: ознакомиться с методами решения задач матричных игр методами линейного программирования.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

М атричная игра представляет собой антагонистическую игру двух лиц с платежной матрицей c т возможными стратегиями первого игрока и n стратегиями второго игрока. Первый игрок стремится максимизировать выигрыш, второй - минимизировать проигрыш. Если матрица игры имеет седловую точку, т.е. существует элемент, являющийся максимальным в столбце и минимальным в строке, то игра имеет решение в чистых стратегиях. В противном случае игра имеет решение в смешанных стратегиях, которые представляют собой вероятностные распределения на множестве чистых стратегий: - смешанная стратегия первого игрока, ;

с мешанная стратегия второго игрока, .

Использование в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш, не меньший чем при использовании им любой другой стратегии; второму игроку - проигрыш не больший чем при использовании им любой другой стратегии.

С точки зрения 1-го игрока игру можно записать как задачу линейного программирования

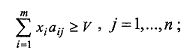
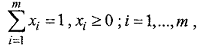
где значение игры V рассматривается как m+1-я переменная, неограниченная по знаку (свободная).

С точки зрения 2-го игрока игру задача имеет вид

Причем обе эти задачи представляют собой пару двойственных задач линейного программирования: решив одну из них, можем найти смешанные стратегии обоих игроков.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Сделать формальную постановку задачи.

2. Определить множество возможных стратегий игроков, при этом по возможности исключить эквивалентные (доминируемые) стратегии.

3. Выписать матрицу игры.

4. Найти оптимальные стратегии игроков, используя симплекс-метод или ЛП в EXCEL.

ЗАДАЧИ ДЛЯ РЕШЕНИЯ