
- •Санкт-Петербург
- •Блок 2. Статистические наблюдения
- •Блок 3. Статистическая информация и статистические показатели
- •Блок 5. Статистические ряды распределения
- •Распределение группы туристов по числу заграничных туров, в которых они побывали
- •Свойства средней арифметической
- •Блок 7. Структурные средние
- •Блок 8. Показатели вариации
- •Блок 9. Изучение формы распределения
- •Ошибки выборочного наблюдения
- •Предельная ошибка выборки
- •Основные виды выборки
- •Блок 11. Малая выборка
- •Характеристики динамики
- •60 Человек на 1 января 2003 г. – это одновременно численность работников фирмы на 31 декабря 2002 г. Поэтому средняя численность работников:
- •Исследование тенденций развития явлений
- •Блок 13. Прогнозирование на основе изучения тренда
- •Агрегатные индексы
- •Блок 15. Индексы средних величин
- •Блок 17. Методы регрессионно-корреляционного анализа связи показателей
- •Критерии согласия
- •Основные формулы
- •Критические значения χ2
- •Перечень вопросов для подготовки к экзамену
- •Список литературы
Критерии согласия
На
практике часто возникает необходимость
произвести оценку близости эмпирических
частот к теоретическим. Такую оценку
можно произвести с помощью критериев
близости, называемых критериями
согласия.
Наиболее часто применяется для этих
целей – критерий
согласия Пирсона
![]() («хи»-
квадрат), который рассчитывается по
формуле:
(«хи»-
квадрат), который рассчитывается по
формуле:
![]()
где f – эмпирические частоты,
![]() -
теоретические частоты.
-
теоретические частоты.
Оценка близости эмпирических частот к теоретическим определяется по вероятности достижения данной величины Р( ) при случайных отклонениях частот. Если вероятность Р( ) значительно отличается от нуля (больше, чем 0,05), то отклонения эмпирических частот от теоретических можно считать случайными. Если Р( )< 0,05, то отклонения нельзя считать случайными, а эмпирическое и теоретические распределения принципиально друг от друга отличаются.
Величина зависит не только от отклонений фактических частот от теоретических, но и от количества групп, на которые разбита совокупность, поэтому таблицы критических значений рассчитаны для различных степеней свободы варьирования эмпирических частот (приложение ). Для нормального распределения число степеней свободы К=n-3, где n – число групп.
Рассмотрим и оценим на примере близость эмпирических и теоретических распределений. Турфирма в течение месяца реализовала 50 путевок. Объем дневной реализации путевок распределился следующим образом (табл.7):
Таблица 7
Число путевок, реализуемых в течение дня |
Фактическая реализация
f |
Теоретическая реализация
|
f- |
(f- )2 |
|
до 3 4 5 6 7 и более
|
5 15 20 7 3 |
4 12 18 12 4 |
1 3 2 -5 -1 |
1 9 4 25 1 |
0,25 0,75 0,22 2,08 0,25 |
Всего: |
50 |
50 |
- |
- |
3,55 |
Таким
образом:
![]() К=5-3=2.
К=5-3=2.
По
таблице критических значений
(приложение ) определяем вероятность
Р(
![]() ,
что значительно превышает 0,05. Это
означает, что отклонения фактических
частот от эмпирических можно считать
случайными, а само распределение
реализации путевок близко к нормальному
распределению.
,
что значительно превышает 0,05. Это
означает, что отклонения фактических
частот от эмпирических можно считать
случайными, а само распределение
реализации путевок близко к нормальному
распределению.
Приложение 1
Основные формулы
Величина равного интервала ,
по формуле Стерджесса .
Средняя арифметическая простая = ,
взвешенная
![]() .
.
Средняя гармоническая простая ͞xh= ,
взвешенная ͞ xh = .
Средняя
квадратическая простая
![]()
взвешенная
 .
.
Средняя
геометрическая
![]() ,
,
Структурные средние:
Мода
Медиана
Показатели вариации:
Размах вариации R= ,
Среднее линейное отклонение для первичного ряда
для вариационного ряда
Среднее квадратическое отклонение для первичного ряда - ,
для вариационного ряда - ,
для
альтернативных признаков -
![]() =
=![]() .
.
Дисперсия для первичного ряда ,
Общая дисперсия по сгруппированным данным
Внутригрупповая дисперсия .
Средняя из внутригрупповых дисперсий .
Межгрупповая дисперсия .
Правило сложения дисперсий .
Коэффициент асимметрии , где - центральный момент третьего порядка определяется как: .
Коэффициент эксцесса , где - центральный момент четвертого порядка.
Средняя ошибка для выборочной средней
Средняя
ошибка выборки для доли
![]()
Темп роста: цепной - ; базисный - .
Темп
прироста: цепной
![]() ;
базисный -
;
базисный -
![]() .
.
Средний
уровень интервального ряда
![]() .
.
Средний
уровень моментного ряда по средней
хронологической
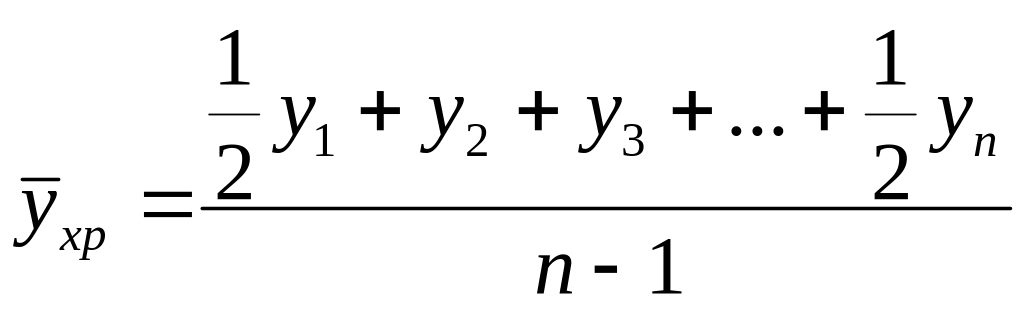 .
.
Индекс физического объема продукции .
Индекс
цен по Пааше 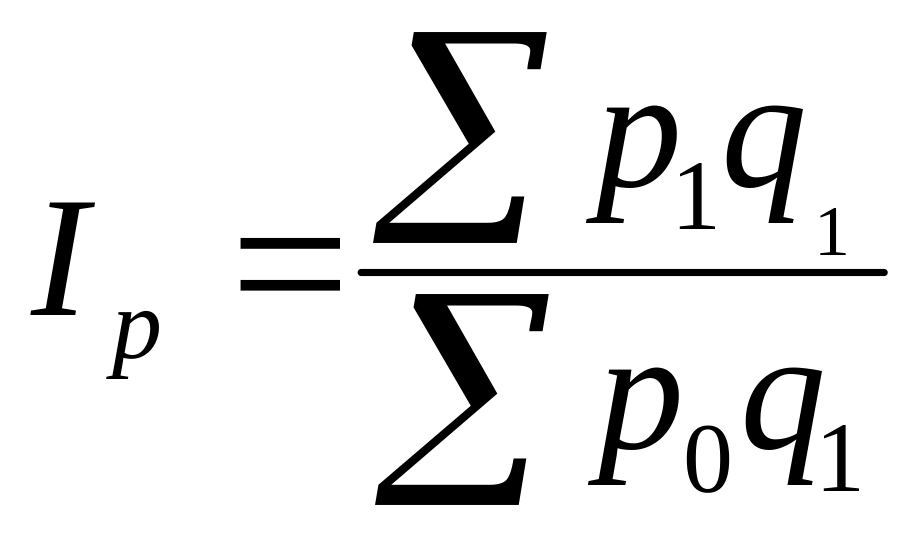 .
.
Индекс цен по Ласпейресу .
Мультипликативная
модель индексов
![]() .
.
Индекс переменного состава : .
Индекс постоянного (фиксированного) состава
Индекс структурных сдвигов .
Соотношение индексов
Уравнение парной линейной регрессии .
Расчет параметров ;
Коэффициент корреляции знаков Фехнера .
Линейный коэффициент корреляции
Индекс корреляции .
Коэффициент
корреляции рангов Спирмена
![]()
Критерий
согласия Пирсона
![]()
Приложение 2
