1.Скалярное произведение векторов

А*В=(a*b)=|a||b|cos(a^b)

Свойство перестановки: a · b = b · a (от перестановки множителей  скалярное   произведение  не меняется);

Свойство распределения: a · (b · c) = (a · b) · c (результат не зависит от порядка умножения);

2.Векторний добуток векторів

A x b=[a.b]= |a||b|sin(a^b)

3.Мішаний добуток векторів

.

Vпар=|(а,в,с)| Vпир= 1/6 |(а,в,с)|

4.Різні типи рівнянь площини

Общее уравнение 

Ax + By + C (  > 0).

Вектор   = (А; В) - нормальный вектор  прямой .

В векторном виде:   + С = 0, где   - радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

5,различные типы прямых на плоскости

А(х-х˳)+В(у-у˳)=0

уравнением первого порядка Ах + Ву + С = 0,

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

6.Расстояние от точки до плоскости.Угол между плоскостями

Пусть Pa = (xa, ya, za)  точка ,  расстояние  от которой необходимо подсчитать.

 Плоскость  можно задать нормалью n = (A, B, C) и одной  точкой  Pb = (xb, yb, zb)

Произвольная  точка  P = (x,y,z) лежит на  плоскости  тогда и только тогда, когда

A x + B y + C z + D = 0

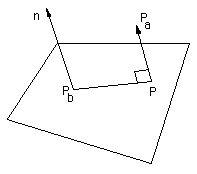
Наименьшее  расстояние  между Pa и  плоскостью  будет равно абсолютной величине выражения

(A xa + B ya + C za + D) / sqrt(A2 + B2 + C2)

Знак самого выражения дает расположение  точки  относительно  плоскости : с какой она стороны.

План решения. Двугранный  угол   между   плоскостями  равен  углу   между  их нормальными векторами   и  . Поэтому  угол     между   плоскостями  определяется формулой

.

Задача 9. Найти  угол   между   плоскостями .

Нормальные векторы заданных  плоскостей

.

Находим

7. Расстояние от точки до прямой в пространстве. Угол между прямыми в пространстве.

Найдём  расстояние  (t) на  прямой  P(x1 ; y1) до плоскости @: Ax + By + C =0

P(x1 ; y1) @ : Ax + By + C = 0 Пусть  точка  M(x0 ; y0) - произвольная  точка  на  прямой . n = {A ; B} - нормальный вектор  прямой  Тогда  расстояние  находится по формуле: d = |Ax1 + By1 + C|/(корень квадратный, под корнем A^2 + B^2)  Расстояние   от   точки  до плоскости:

Найдём d ; P(x1 ; y1 ; z1) до @ : Ax + By + Cz + D = 0

 Расстояние  находится по формуле: d = |Ax1 + By1 + Сz1 + D|/(корень квадратный, под корнем A^2 + B^2 + C^2)  Расстояние   от   точки   до   прямой   в   пространстве :

Найдём  расстояние  (d), P(x1 ; y1 ; z1)  до   прямой  l: (x-x0)/m = (y-y0)/n = (z-z0)/p

Доказ-во: Выберем произволную  точку  M0 (x0 ; y0 ; z0) на  прямой  и начало направляющего вектора S совместим с этой  точкой . На векторах M0P , S построим параллелограмм (M0PCB). ОЧевидно, что (d)- расстояние - это высота M0PCB. - C одной стороны S(площадь)=|S(вектор)| * d - С другой стороны S(площадь)=|S(вектор) х M0P(вектор)|  Расстояние  находится по формуле: d = |S(вектор) х MoP(ан-но)|/|S(вектор)|

Угол   между   прямыми   в   пространстве  равен  углу   между  их направляющими векторами. Поэтому, если две  прямые  заданы каноническими уравнениями вида

 и      косинус  угла   между  ними можно найти по формуле:

8.Расстояние между 2 прямыми в пространстве

 Имеются 4 вектоpа : P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3) и P4(x4,y4,z4), котоpые задают в тpехмеpном  пpостpанстве , соответственно, 4 точки (P1,P2,P3 и P4). Чеpез точки P1 и P2 пpоходит  пpямая  l1, чеpез P3 и P4 - l2. Hужно найти  pасстояние   между  этими  пpямыми  ( то есть, пеpпендикуляp минимальной длины, опущенный из какой-то точки одной  пpямой  на дpугую пpямую ).

l1: x-x0/a1=y-y0/b1=z-z0/c1, l2: x-x1/a2=y-y1/b2=z-z1/c2. a={a1, b1, c1}, b={a2, b2, c2} - направляющие векторы l1 и l2 соответственно, тогда расстояние d между l1 и l2 определяется по формуле d=|(M1M0×a)•b|/|a×b|.

  9.Элипс

 геометрическое место точек MЕвклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

| F1M | + | F2M | = 2a, причем | F1F2 | < 2a. Окружность является частным случаем  эллипса . Наряду с гиперболой и параболой,  эллипс  является коническим сечением иквадрикой.  Эллипс  также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекциюокружности на плоскость.

Оптические

Свет от источника, находящегося в одном из фокусов, отражается  эллипсом  так, что отраженные лучи пересекутся во втором фокусе.

Свет от источника, находящегося вне любого фокусов, отражается  эллипсом  так, что отраженные лучи ни в каком фокусе не пересекутся.

Если F1 и F2 — фокусы  эллипса , то для любой точки X, принадлежащей  эллипсу , угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой(F2X).

Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими  эллипс , всегда будет проходить через центр  эллипса . Это позволяетпостроением с помощью циркуля и линейки легко получить центр  эллипса , а в дальнейшем оси, вершины и фокусы.

Эволютой  эллипса  является астроида.

Точки пересечения  эллипса  с осями являются его вершинами.

Эксцентриситет  эллипса  равен отношению  . Эксцентриситет характеризует вытянутость  эллипса . Чем эксцентриситет ближе к нулю, тем  эллипс  больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

 Эллипс  также можно описать как

фигуру, которую можно получить из окружности, применяя аффинное преобразование

ортогональную проекцию окружности на плоскость

Пересечение плоскости и кругового цилиндра

10.Гипербола

 геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно.  Гиперболу , у которой a = b, называют равнобочной. Равнобочная  гипербола  в некоторой прямоугольной системе координат описывается уравнением

xy = a2 / 2,

при этом фокусы  гиперболы  располагаются в точках (a, a) и (−a,−a).

 Гиперболы , связанные с треугольником

 гипербола  Енжабека — кривая, изогонально сопряженная прямой Эйлера;

 гипербола  Киперта — кривая, изогонально сопряженная прямой проходящей через точка Лемуана и центр описанной окружностиданного треугольника.

Оптическое свойство. Свет от источника, находящегося в одном из фокусов  гиперболы , отражается второй ветвью  гиперболы  таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

Иначе говоря, если F1 и F2 фокусы  гиперболы , то касательная в любой точки X  гиперболы  является биссектрисой угла  .

Для любой точки лежащей на  гиперболе  отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

 Гипербола  обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра  гиперболы .

Каждая  гипербола  имеет сопряженную  гиперболу , для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей  гиперболу . Сопряженная  гипербола  не является результатом поворота начальной  гиперболы  на угол 90°; обе  гиперболы  различаются формой.

]Асимптоты

Две сопряженные  гиперболы (голубая и зеленая) обладают совпадающими асимптотами (красные). Эти  гиперболы  единичные и равнобочные, так как a = b = 1.

 Гипербола , в её каноническом виде, задается парой функций:

имеет две асимптоты

.

11.Парабола

 геометрическое место точек, равноудалённых от данной прямой (называемойдиректрисой  параболы ) и данной точки (называемой фокусом  параболы ).

Каноническое уравнение  параболы  в прямоугольной системе координат:

 (или  , если поменять местами оси).

Квадратное уравнение   при   также представляет собой  параболу  и графически изображается той же  параболой , что и  , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке  , координаты которой вычисляются по формулам:

 где D = b2 − 4ac - дискриминант

Уравнение   может быть представлено в виде  , а в случае переноса начала координат в точку   каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.

12. Цилиндрические поверхности

 поверхность , получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть  поверхности  цилиндра, ограниченная  цилиндрической   поверхностью  называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом граница основания будет по форме совпадать с направляющей. различают эллиптический цилинд р, канонич. уравнение к-рого    мнимый эллиптический цилиндр:    гиперболический цилиндр:    параболическнй цилиндр:   

13. Конические поверхности

  поверхность , с вершиной O и направляющей G, содержащая все точки всех прямых, проходящих через точку O и пересекающихся с кривой G.

Каноническое уравнение круговой  конической   поверхности  в декартовых координатах  .

 множество прямых (образующих), проходящих через данную точку (вершину  конической   поверхности ) и пересекающих данную кривую (направляющую). Если направляющая - окружность, а вершина  конической   поверхности  лежит на перпендикуляре (оси  конической   поверхности ) к плоскости окружности, проходящем через ее центр, то  коническая   поверхность называется круглым конусом; он состоит из двух полостей, соединяющихся в его вершине.

14.Эллипсоида. Однопорожнинний та двопорожнинний гіперболоїд.

 Эллипсоида  вращения планетарного (полуось экваториальная а, полуось вращения с; c< a)

где логарифм натуральный.

 Эллипсоида  вращения удлиненного (полуось экваториальная b, полуось вращения a; а > b)

.

 Эллипсоида  о трех неравных главных полуосях (а > b > с)

F(λ,k) и E(λ,k) суть эллиптические интегралы первого и второго вида:

Однопорожнинний  і  двопорожнинний   гіперболоїди.

При обертанні гіперболи  навколо осі (яка її не перетинає) одержимо поверхню, яка називається однопорожнинним   гіперболоїдом  обертання.            В результаті стиску цієї поверхні по осі  ми отримаємо поверхню, що називається однопорожнинним   гіперболоїдом Через кожну точку  однопорожнинного   гіперболоїда  проходять дві прямі (прямолінійні твірні)     Дійсно, перемноживши два рівняння і скоротивши на, отримаємо  тобто рівняння  однопорожнинного  гіперболоїда . А це значить, що всі точки прямих ліній при всеможливих значеннях  і  лежать на однопорожнинному   гіперболоїді .         Такі ж  міркування можна провести і для сімейства прямих.           Поверхня, що складається із прямих ліній, називається лінійчатою поверхнею. Отже, однопорожнинний   гіперболоїд  – приклад лінійчатої поверхні.             Якщо обертати гіперболу  навколо осі  (осі, яка її перетинає), то отримаємо поверхню, що називається  двопорожнинним   гіперболоїдом  обертання. Рівняння цієї поверхні В результаті стиску цієї поверхні одержимо поверхню з рівнянням Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння вигляду називається двопорожнинним   гіперболоїдом . Двом віткам гіперболи відповідають дві не зв’язані між собою частини поверхні. 

15. Еліптичний та гіперболічний параболоїд

Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння називається еліптичним   параболоїдом  Відмітимо, що перерізи  еліптичного   параболоїда площинами, що перпендикулярні осі представляють собою еліпси, а площинами, що паралельні площинам  та  параболи.

Поверхня, що має в деякій прямокутній декартовій системі координат рівняння

називається  гіперболічним   параболоїдом  . Її ще називають сідлом.

 Гіперболічний   параболоїд  будується таким чином: задаються дві параболи і одна з них переміщується так, щоби її вершина ковзала по другій, причому обидві осі парабол паралельні, параболи знаходяться у взаємно перпендикулярних площинах і їх вітки направлені в протилежні сторони. При такому переміщенні рухома парабола описує  гіперболічний   параболоїд .

Переріз  гіперболічного   параболоїда  площиною, що перпендикулярна осі представляє гіперболу При цьому, якщо дійсна вісь гіперболи паралельна осі а при дійсна вісь гіперболи паралельна осі При гіпербола вироджується в пару прямих, що перетинаються.

 Гіперболічний   параболоїд  теж є лінійчатою поверхнею. Як і однопорожнинний гіперболоїд, він має два сімейства прямолінійних твірних, рівняння яких можна записати у вигляді

Виводяться ці рівняння аналогічно, як це було зроблено для одно порожнинного гіп

ерболоїда.

16. Визначники 2-го та 3-го порядків. Означення. Теореми розкладання та анулювання

17. Матрицы. Действия над матрицами

 система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m × n)- матрице . Обозначения:

        

         или 

        Короче:

Действия над  матрицами . Произведением прямоугольной (m × n)- матрицы  А на число ее называют М., элементы которой получены из элементов aij умножением на число α:

         

         Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть

         

         Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением (m × р)- матрицы  А на (р × n)- матрицу  В будет (m × n)- матрица  С с элементами

         cij = ai1b1j + ai2b2j + ... + aipbpj,

         i = 1, ..., m, j = 1, ..., n.

         Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство AB = BA может не выполняться.  Матрицы  А и В называются перестановочными, если AB = BA. Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой. Справедливы правила:       

18. Обернена матриця. Властивості обернених матриць

Аˉ¹=1\det А(А11 А21 А31

А21 А22 А32

А13 А23 А33)

 — операція обернення є інволюцією.

 — обернення транспонованої  матриці 

 — обернення спряженої  матриці 

 для довільного коефіцієнта 

 — визначник  оберненої   матриці .

 — ранг  матриці  дорівнює розміру  матриці .

Точні методи

Метод Гауса — Жордана

LU розклад  матриці 

де   —

 союзна  матриця .

19.Ранг матрицы.Минор.Элементарные преобразование матриц. Метод элементарных преобразований для нахождения ранга.

Ранг   матрицы  — наивысший из порядков миноров этой  матрицы , отличных от нуля. Обычно  ранг   матрицы  A обозначается   ( ) или  .  Минор  k -го порядка  матрицы  (от лат. minor – меньший) – определитель  матрицы , составленный из элементов данной  матрицы , стоящих на пересечении произвольно выделенных ее k строк и k столбцов с сохранением их порядка, т.е.  минор  k-го порядка есть определитель квадратной  матрицы  размера k x k.

Каждая n x m  матрица  имеет    миноров  k-го порядка.  Минорами  1-го порядка являются элементы  матрицы . Если номера строк, в которых расположен  минор , совпадают с номерами столбцов, то он называется главным  минором .

 Элементарные   преобразования   матрицы  — это такие  преобразования   матрицы , в результате которых сохраняется эквивалентность  матриц . Таким образом, элементарные   преобразования  не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта  матрица .  Элементарными   преобразованиями  строк называют:

перестановка местами любых двух строк  матрицы ;

умножение любой строки  матрицы  на константу  ,  ;

прибавление к любой строке  матрицы  другой строки, умноженной на константу  ,  .

В некоторых курсах линейной алгебры перестановка местами двух строк  матрицы  не вносятся в определение  элементарных   преобразований  так как перестановку местами любых двух строк  матрицы  можно получить используя умножение любой строки  матрицы  на константу  ,   и прибавление к любой строке  матрицы  другой строки, умноженной на константу  ,  .

 Элементарными   преобразованиями   матрицы  называют следующие:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

4. Вычёркивание строки (столбца), все элементы которой равны нулю.

З а м е ч а н и е . 1)  Элементарные   преобразования  не меняют  ранга   матрицы ; 2)  матрицы , полученные одна из другой путём  элементарных   преобразований , называются эквивалентными (обозначаются A ~ В).

Чтобы вычислить  ранг   матрицы  А, путём  элементарных   преобразований  сводим её к ступенчатому виду (в частности к треугольному), выделяя наибольший минор, отличный от нуля.

A~

rangA = rangB= k