24. Сходимость последовательности точек в Rn, ее эквивалентность покоординатной сходимости.

Пусть 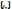– последовательность точек в Rⁿ. Мы говорим, что эта последовательность сходится к точке p0, если числовая последовательность 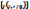имеет предел 0.

Пусть p₁=(x₁,y₁), p₂=(x₂,y₂) ,…- последовательность точек в . Мы скажем, что эта последовательность сходится к точке p₀=(x₀,y₀), если числовая последовательность x₁,x₂,… сходится к числу x₀, а числовая последовательность y₁,y₂,… - к числу y₀.

25. Функция нескольких переменных.

Числовая ф-ция n переменных характеризуется тем, что областью ее определения является подмножество Х пространства Rⁿ, n>1В этом случае значение аргумента х представляет собой точку (х₁,х₂,..х_n) . x – независимые переменные, y – зависимые(функция).

26. Поверхности (линии) уровня функции нескольких переменных.

Ф-ция z=f(x,y); график – поверх-ть в R3. Линией уровня ее назыв линию на пл-ти xOy, во всех точках кот. функция f принимает постоянное значение C. Для заданного с удовлет: f(x,y)=с.

Для ф-ции 3х перем u=f(x,y,z) ур-ние f(x,y,z)=с при фиксир константе с определяет пов-ть в R3, кот назыв пов-тью уровня ф-ции.

При n>2 следует говорить не о линиях, а о множествах уровня. Множество уровня имеет уравнение f( и истолковывается как “ поверхность” в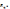

27. Предел функции нескольких переменных.

Пусть на множестве X Rⁿ задана функция f(P) и пусть p₀ – предельная точка для D(f). Число a называется пределом функции f(P) в точке P₀, если для любой сходящейся к p₀ последовательности из D(f), сходящихся к P₀,но отличных от него, справ-во соот-ние: lim k→∞f(P_k)=a, при этом

Lim P→ P₀ f(P)=a.

28. Непрерывность функции нескольких переменных.

Ф-ция n перем-х f(P), определенная на множестве X Rⁿ, называется непрерывной в точке P₀  D(f) , если lim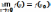 P→ P₀ f(P)=f(P₀), или же, если P₀ – изолир точка множества D(f) . Функция f(P), опред на множестве X Rⁿ, назыв непрерывной на этом множестве, если она. непрерывна в каждой точке множества Х.

29. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.

Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х Rⁿ, то она ограничена на этом множестве.

Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х Rⁿ, то существует точка p1  X, в которой f принимает свое наименьшее значение, и точка p2  X, в которой f принимает свое наибольшее значение на Х. fнаим=f(P1)<=f(P)<= f(P2)=fнаиб.

30. Частные производные функции нескольких переменных.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.

Частные производные функции z=f(x,y) в точке (x₀,y₀) обозначаются так:

z’x , dz/dx , f’x(x₀,y₀) – производная по x;

z’y, dz/dy, f’y(x₀,y₀) – производная по y.

…назыв величина lim Δx→0 (f(x₀+Δx; y₀)-f(x₀; y₀))/Δx= df/dx(d закругл) (x₀; y₀)

31.Диффер-ть функции неск перем-х.

Функция z=f(x;y) называется дифференцируемой в точке (x0,y0), если ее полное приращение можно представить в виде Δz=f(x,y)-f(x₀; y₀)= f’_x(x₀; y₀) Δx+ f’_y(x₀; y₀) Δy+ εp или Δz=dz+ εp, где ε=ε(Δx, Δy) a-ция беск малая при Δx, Δy→0, p=√(Δx)²+ (Δy)². Расстояние от Δx до Δy.

Если функция дифференцируема в точке, то она непрерывна в этой точке.

32. Дифференциал функции нескольких переменных.

Линейная часть полного приращения функции называется полным дифференциалом и обозначается dz:

Δz=f(x₀+Δx; y₀₊Δy)- f(x₀; y₀)-полное приращение ф-ции в т. (x₀; y₀). Роль линейного приближения выполняет полный диф-ал ф-ции. dz= z’_x Δx+ z’_y Δy

33. Достаточное условие дифференц-ти функции нескольких переменных.

Пусть F(x) имеет все частные производные в окрестности точке  х_о  , непрерывные в самой этой точке. Тогда функция дифференцируема в точке  х_о .

Ф-ция z=f(x,y) диф-ма в т. (x₀; y₀), если f’_x и f’_y опред-ны в окр-ти т. (x₀; y₀) и непрер-ны там.

34. Непрерывность дифференцируемой функции.

Функция, дифференцируемая в точке  х_o − непрерывна в этой точке. Док-во: ф-ция диф-ма в т. (x₀; y₀), поэтому Δz=dz+ εp. lim Δx, Δy→0 Δz=lim Δx, Δy→0(z’_x Δx+ z’_y Δy)+ lim Δx, Δy→0 εp=0. Lim Δx, Δy→0 (f(x₀+Δx; y_{0 +} Δy)-f(x₀; y₀))=0 следует они равны.

35. Дифференцируемость сложной функции.

Если ф-ция х=φ(t) и у=ψ(t) дифференцируемы в точке t₀, а ф-ция z=f(x,y) дифференцируема в точке (φ(t₀), ψ(t₀)), то сложная ф-ция F(t)=f(φ(t), ψ(t)) также дифференцируема в t_0. При этом производная сложной ф-ции находится по формуле F’(t₀)=f’_x(φ(t₀), ψ(t₀)) φ’(t₀)+ f’_y(φ(t₀), ψ(t₀)) ψ’(t₀)

36.Производная по направлению.

Производной ф-ции f(x,y) в точке (x₀,y_o) по направлению ℮ называется предел

Справедлива фор-ла: (начало как в фор-ле выше)= f’_x(x₀; y₀)cosа+ f’_y(x₀; y₀)cosb

Скорость изменения ф-ции по направлению е.

37. Градиент. Свойства градиента.

Градиентом ф-ции z= f(x,y) в точке M(x,y) называется вектор, координаты которого равны соответствующим частным производным z’_x ,z’_y , взятым в точке M(x,y).

Свойства:

1)Вектор grad f(M) указывает на направление наиболее быстрого роста функции в точке М, а его длина равна скорости этого роста.

2)В каждой точке градиент перпендикулярен линии (поверхности) уровня, проходящей через эту точку.

df/de(вектор)=(gradf,e)(с векторами)=модуль grad(вектор)модуль e(вектор) cos фи; если cos фи=1, то направления градиента и «е» совпадают.

38.Эластичность функции нескольких переменных.

Δ_x z=f(x₀+Δx; y₀)-f(x₀; y₀) – частн приращ-ие

Эласт-тью ф-ции z=f(x,y) в т. (x₀; y₀) по x называется lim Δx→0((Δ_x z)/z : Δx/x)= E_zx (x₀; y₀). lim Δy→0((Δ_y z)/z : Δy/y)= E_zy (x₀; y₀). E_zx = z’_x x/z = x(lnz)’_x. E_zy = z’_y y/z = y(lnz)’_y.

39.Однородные функции.

XC Rⁿ (x1…xn)принад X, следовательно, (tx1…txn)принад X, t>0, f(x,y) определена на X. Ф-ция f(x,y) называется однородной, если для любого t>0 f(tx,ty)= t^альфаf(x,y).

40. Формула Эйлера для однородной функции.

Пусть дифференцируемая функция f- однородная функция переменных степени , тогда справедлива формула Эйлера:

(общий случай)

(n=2)

41.Частные производные высших порядков.

Частной производной n-го порядка функции многих переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции.

z=f(x,y); f’_x и f’_y - произ 1ого порядка. f’’_xx = (f’_x)’_x и т.д.

42. Теорема о равенстве смешанных производных

Если производные и 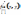сущест­вуют в некоторой окрестности точки М(х₀, у₀) и непрерывны в самой точке М, то имеет место равенство

(М)=(М)

43. Локальные экстремумы функций

нескольких переменных.

Точка М называется точкой локального минимума функции у=f(x), если существует такая окрестность М, что в любой точке Xэтой окрестности выполняется неравенство f(М) <= f(X).

Аналогично точка М называется точкой локального максимума функции y = f (X), если существует такая окрестность М, что в любой точке X этой окрестности выполняется неравенство f(М) >= f(X).

Точки локальных минимумов и максимумов функции у=f(X) называются точками локальных экстремумов данной функции