Симплексный метод решения матричных игр

Если у каждого из игроков больше двух возможных стратегий, то можно решение игры свести к решению задачи линейного программирования.

Рассмотрим игру, матрица которой не содержит седловой точки. Поэтому решение игры представим в смешанных стратегиях:

, ,

где , , .

При оптимальной стратегии игроку 1, обеспечен выигрыш независимо от выбора стратегий 2 игроком, то есть

(при стратегии В₁)

(при стратегии В₂)

(при стратегии В_n)

Цена игры неизвестна, но можно предположить . Последнее условие выполняется, если элементы игровой матрицы неотрицательны, а этого можно достигнуть, прибавляя ко всем элементам матрицы некоторое положительное число. Преобразуем систему ограничений, разделив обе части неравенства на и вводя обозначения: .

В результате получим:

Первый игрок стремится цену игры максимизировать, значит, функция должна принимать минимальное значение. Таким образом, получи-лась задача линейного программирования.

Для определения стратегии 2 игрока задача линейного программирования будет иметь после аналогичных преобразований и замены переменных следующий вид:

, где .

Таким образом, для решения игры имеем пару двойственных задач линейного программирования. Из них удобнее решать задачу на максимум с ограничениями ‘ ’ симплексным методом.

Пример 10. Найти решение игры, определяемой матрицей:

.

Решение. Элементы платежной матрицы имеют отрицательные числа, к каждому элементу матрицы А прибавим единицу и получим следующую матрицу, все элементы которой неотрицательны:

.

Эта игра не содержит седловой точки, решением игры являются смешанные стратегии и c ценой , для определения которых составим теперь пару взаимно-двойственных задач:

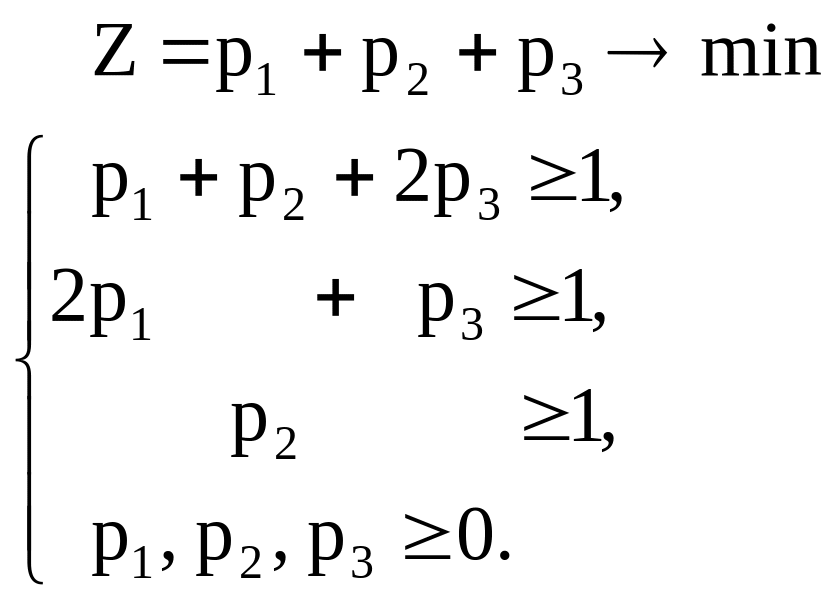
для первого игрока для второго игрока

(при стратегии В₁) (при стратегии А₁)

(при стратегии В₂) (при стратегии А₂)

(при стратегии В₃) (при стратегии А₃)

Решим симплексным методом (см. пример 4) вторую из пары взаимно-двойственных задач на максимум (табл. 25–27), где ограничения имеют знак ‘ ’. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

Линейную функцию F представим в виде

.

Таблица 25

Базисные переменные	Свободные члены	q1	q2	q3	q4	q5	q6	Оценочное отношение
q4	1	1	2	0	1	0	0	∞
q 5	1	1	0	1	0	1	0
q6	1	2	1	0	0	0	1	∞
F	0	– 1	– 1	– 1	0	0	0

Таблица 26

Базисные переменные	Свободные члены	q1	q2	q3	q4	q5	q6	Отношение
q 4	1	1	2	0	1	0	0
q3	1	1	0	1	0	1	0	∞
q6	1	2	1	0	0	0	1
F	1	0	– 1	0	0	1	0

Таблица 27

Базисные переменные	Свободные члены	q1	q2	q3	q4	q5	q6
q2	1/2	1/2	1	0	1/2	0	0
q3	1	1	0	1	0	1	0
q6		3/2	0	0	–1/2	0	1
F	3/2		0	0		1	0

Из последней симплекс–таблицы, определяющей оптимальный план, следует, что F_max = 3/2

при ,

а из соотношений двойственности следует, что

.

Следовательно, цена игры с платежной матрицей А₁

,

а для исходной игры с платежной матрицей А:

.

При этом оптимальные стратегии игроков имеют вид

;

63