
- •Е.Г. Романова Дифференциальная геометрия
- •Содержание
- •1. Векторная функция скалярного аргумента
- •1.1. Определение вектор-функции. Предел. Непрерывность
- •1.2. Дифференцирование вектор-функции
- •1.3. Интеграл от векторной функции по скалярному аргументу
- •2. Сведения из теории кривых
- •2.1. Элементарная кривая
- •2.2. Касательная прямая к кривой
- •2.3. Соприкасающаяся плоскость кривой
- •2.4. Длина дуги как параметр
- •2.5. Кривизна кривой
- •2.6. Кручение кривой
- •2.7. Формулы Френе
- •3. Теория поверхностей в дифференциальной геометрии
- •3.1. Элементарная поверхность
- •3.2. Регулярная поверхность
- •3.3. Кривые на поверхности
- •3.4. Касательная плоскость и нормаль к поверхности
- •3.5. Измерение на поверхности длин, углов, площадей. Первая квадратичная форма поверхности
- •3.6. Площадь поверхности
- •3.7. Вторая квадратичная форма поверхности
- •3.8. Кривизна кривой, лежащей на поверхности
- •3.9. Главные направления и кривизны поверхности
- •3.10. Внутренняя геометрия поверхности
- •Литература:
3.2. Регулярная поверхность
Пусть Ф
– элементарная поверхность, заданная
уравнением
![]() .
.
Определение
3.3.
Поверхность
Ф
называется
регулярной
(k
раз
дифференцируемой),
если функции
x,
y,
z
имеют
непрерывные,
частные
производные до порядка k
включительно,
причём в каждой точке
![]() ранг матрицы
А
=
ранг матрицы
А
=
 равен
двум.
равен
двум.
При k = 1 поверхность называется гладкой.
Замечание 3.2.
Частные
производные
![]() ,
,
![]() и т.д. функций
x,
y,
z
будем
обозначать
и т.д. функций
x,
y,
z
будем
обозначать
![]() .
Таким образом,
.
Таким образом,
![]() ,
,
![]() .
.
Найдём частные
производные радиус–вектора
![]() по u
и v:
по u
и v:
![]() ,
,
![]() .
.
Тогда матрица А
примет вид A
=
![]() и состоит из координат векторов
и состоит из координат векторов
![]() и
и
![]() .
Условие, что ранг A
равен двум
означает, что векторы
и
не коллинеарны. Далее будем рассматривать
только такие векторы.
.
Условие, что ранг A
равен двум
означает, что векторы
и
не коллинеарны. Далее будем рассматривать
только такие векторы.
Как известно,
из курса математического анализа, если
функции x(u,
v)
и y(u,
v)
удовлетворяют условию
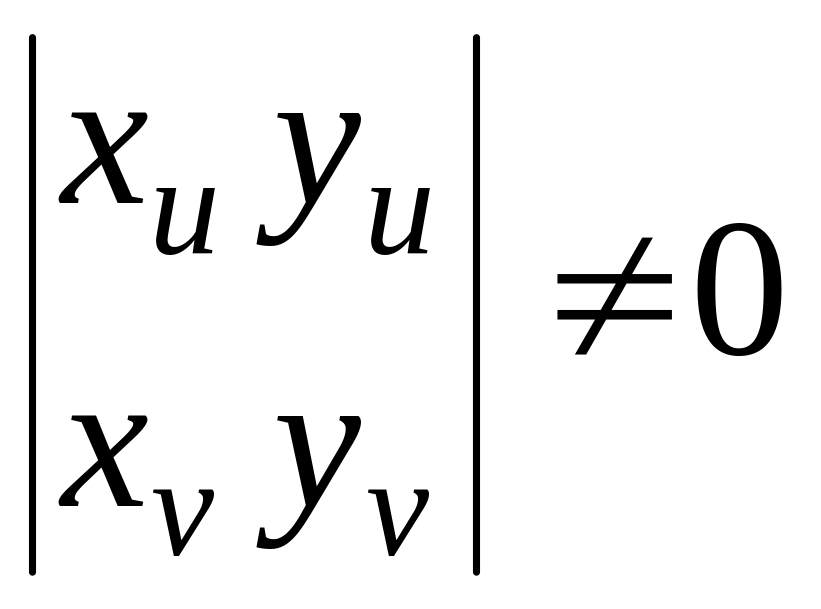 ,
то вблизи данных значении u,
v
и соответствующих им значении x
и y
уравнения x=x(u,
v)
и y=y(u,
v)
могут быть разрешены относительно u,
v.
Таким
образом, u=u(x,
y),
v=v(x,
y)
и получаем
,
то вблизи данных значении u,
v
и соответствующих им значении x
и y
уравнения x=x(u,
v)
и y=y(u,
v)
могут быть разрешены относительно u,
v.
Таким
образом, u=u(x,
y),
v=v(x,
y)
и получаем
![]() или
или
![]() – уравнение поверхности в явном виде.
– уравнение поверхности в явном виде.
3.3. Кривые на поверхности
Рассмотрим
на поверхности F
множество точек, криволинейные координаты
которых определяются уравнениями:
u=u(t),
v=v(t),
где t
– независимая
переменная. Тогда векторная функция
каждой точки поверхности может быть
записана в виде:
![]() .
При изменении параметра, вектор
описывает своим концом некоторую кривую
в пространстве, тем самым кривую
на поверхности
F.
.
При изменении параметра, вектор
описывает своим концом некоторую кривую
в пространстве, тем самым кривую
на поверхности
F.
В параграфе 3.1 построена, так называемая сеть кривых на поверхности или координатная сеть.
3.4. Касательная плоскость и нормаль к поверхности
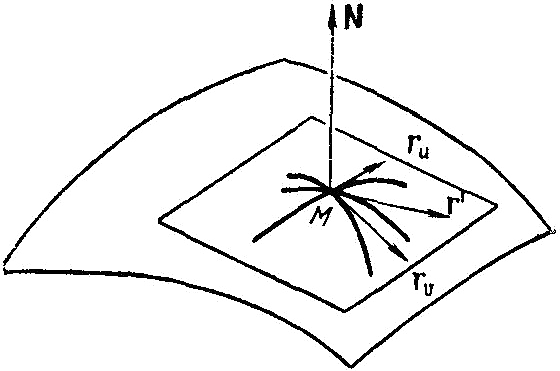
Рисунок
7![]() и
и
![]() лежат
в касательной плоскости, вектор
лежат
в касательной плоскости, вектор
![]() нормален
к ней и уравнение этой плоскости имеет
вид:
нормален
к ней и уравнение этой плоскости имеет
вид:
![]() ,
(3.2)
,
(3.2)
здесь
–
радиус-вектор
точки касания,
![]() –
радиус-вектор
текущей точки касательной плоскости.
–
радиус-вектор
текущей точки касательной плоскости.
Пусть
поверхность задана уравнением
![]() ,
т.
е. в векторной форме
.
Напишем
уравнение касательной плоскости для
такой поверхности. Имеем
,
т.
е. в векторной форме
.
Напишем
уравнение касательной плоскости для
такой поверхности. Имеем
![]() ,
,
![]()
и, следовательно,
![]() .
(3.3)
.
(3.3)
Подставив
в уравнение касательной плоскости (3.2)
вместо
![]() вектор
вектор
![]() ,
а вместо нормального вектора
,
а вместо нормального вектора
![]() его
выражение (3.3), получим уравнение
касательной плоскости
к поверхности
в
точке
его
выражение (3.3), получим уравнение
касательной плоскости
к поверхности
в
точке
![]() :
:
(3.4)
где
значения производных
![]() и
и
![]() берутся
в точке касания
берутся
в точке касания
![]() .
.
Если
поверхность задана неявным уравнением
![]() ,
которое
определяет
,
которое
определяет
![]() как дифференцируемую функцию от x
и
y,
то
как дифференцируемую функцию от x
и
y,
то
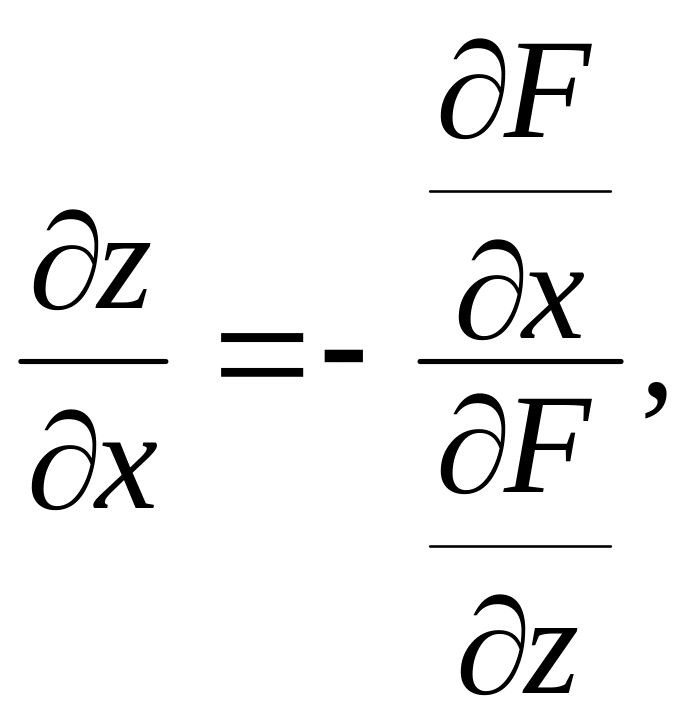
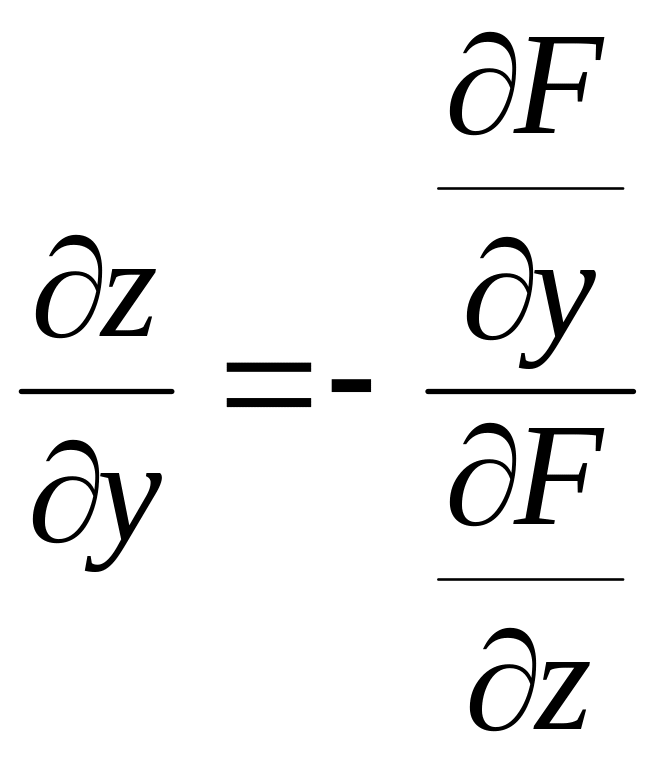 .
.
Подставив эти выражения в уравнение (3.4), получаем уравнение плоскости, касательной к поверхности :
![]() .
(3.5)
.
(3.5)
Здесь
значения![]() ,
,
![]() и
и
![]() берутся
в точке касания
.
берутся
в точке касания
.
Нормаль к поверхности. Пусть F (x, y, z) = 0 – неявное уравнение поверхности. Нормаль к поверхности (перпендикулярная прямая к касательной плоскости в точке касания) имеет вид:
![]() .
.
Вычислим
направляющие косинусы вектора ,
нормального
к поверхности, заданной уравнением
![]() .
Так как
.
Так как
![]() и
и
![]() ,
,
то
вектор
![]() имеет
координаты
имеет
координаты
(3.6)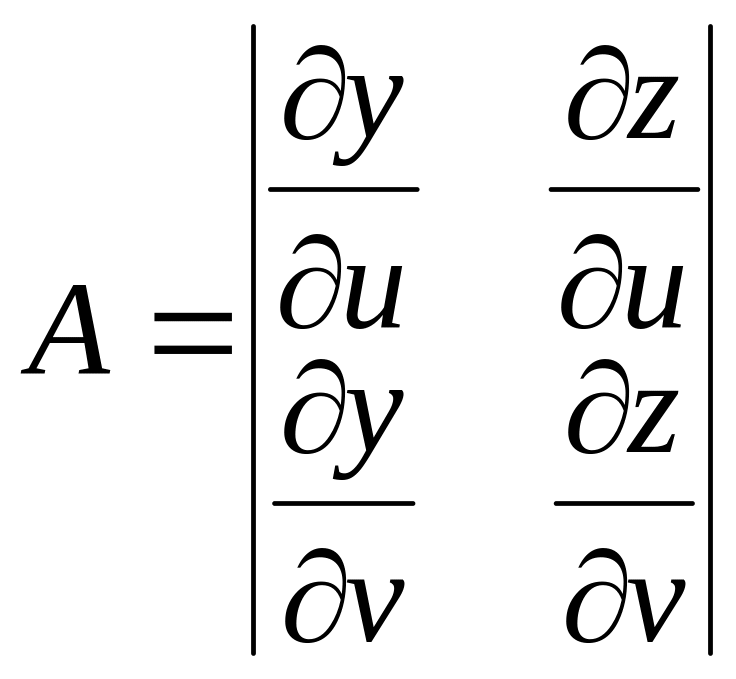
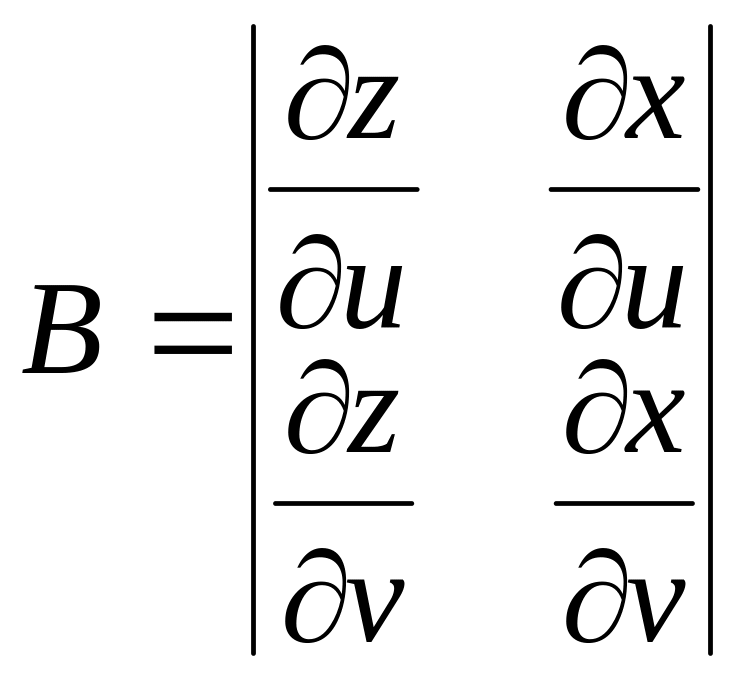 ,
,
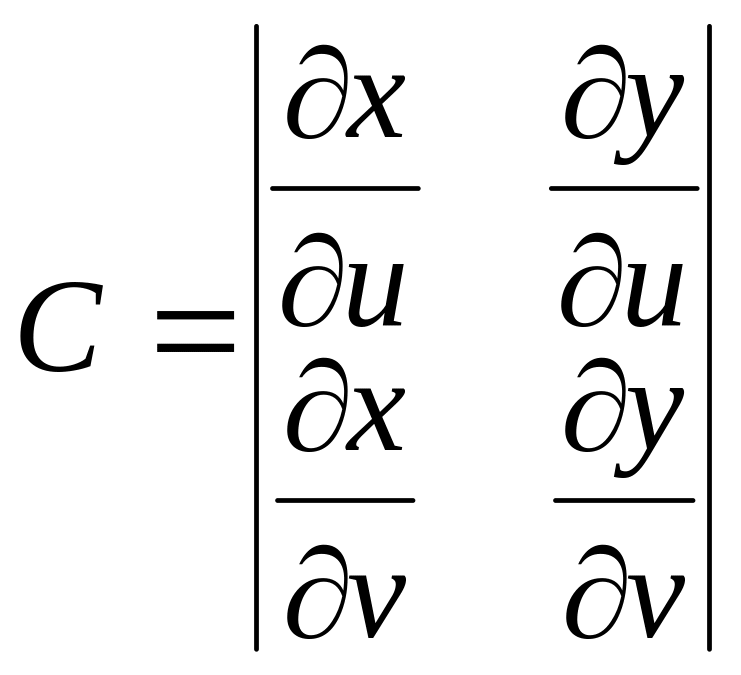 ,
,
а его направляющие косинусы соответственно равны
![]() ,
,
![]() ,
,
![]()
