
2 Интегрирование
Квадратурные формулы Гаусса, определение параметров квадратурных формул, используя ортогональные полиномы. Свойства, погрешность.
Квадратурные формулы Гаусса (формулы наивысшей алгебраической точности) получают из формул Ньютона-Котесса посредством оптимизации распределения узлов.
В общем случае формулы для приближенного вычисления определенного интеграла
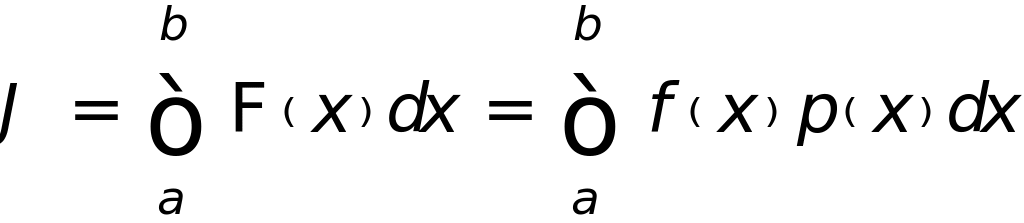
(![]() - весовая функция) получаются заменой
подынтегральной функции интерполяционным
полиномом с последующим аналитическим
интегрированием для вычисления
квадратурных коэффициентов
- весовая функция) получаются заменой
подынтегральной функции интерполяционным
полиномом с последующим аналитическим
интегрированием для вычисления
квадратурных коэффициентов
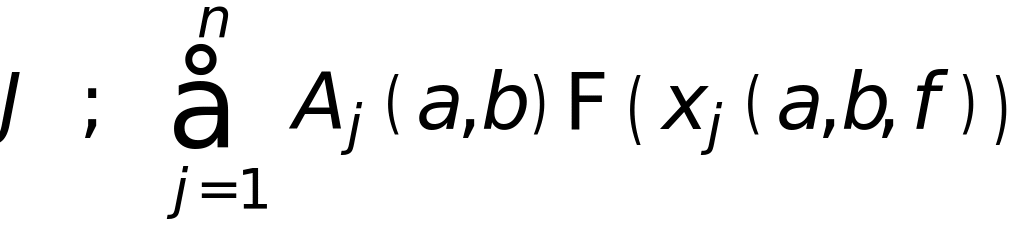
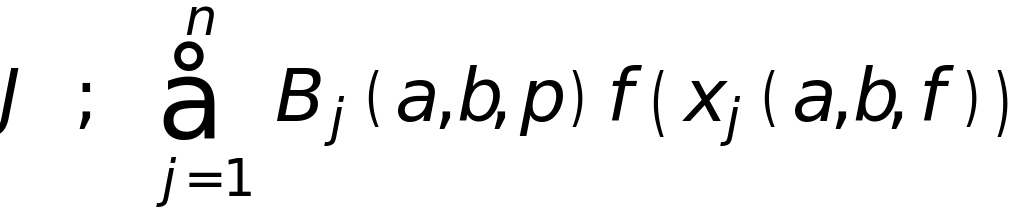
где
![]() - узлы
квадратурной формулы, а
- узлы
квадратурной формулы, а
![]() коэффициенты,
которые не
зависят от подынтегральной
функции и могут быть предварительно
вычислены для каждого распределения
узлов.
коэффициенты,
которые не
зависят от подынтегральной
функции и могут быть предварительно
вычислены для каждого распределения
узлов.
В формулах Ньютона-Котесса выбирается эквидистантное распределение узлов. Оценка погрешности интегрирования
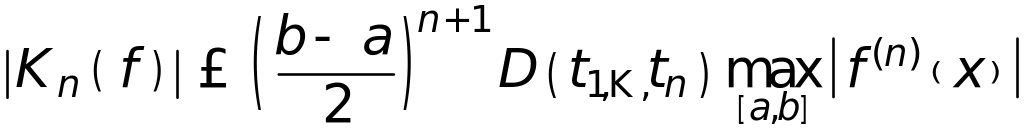
Из формулы следует, что формула Ньютона-Котесса позволяет точно интегрировать полиномы степени
Для кв.формул Гаусса узлы выбираются в корнях ортогональных полиномов. Оценка погрешности
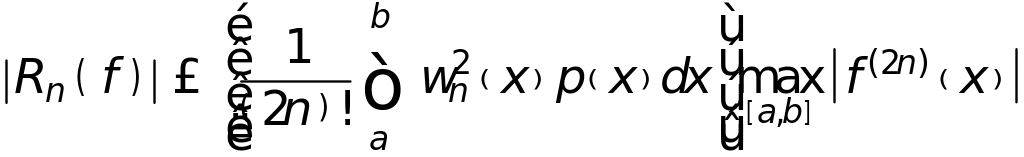
где
![]() - используемый ортогональный полином
с такой нормировкой, что коэффициент
при старшей степени равен 1
- используемый ортогональный полином
с такой нормировкой, что коэффициент
при старшей степени равен 1
т.е. формула Гаусса
позволяет точно интегрировать
полиномы степени
![]()
Обычно
![]()
Построение рабочих кв.формул Гаусса основано
на предположении, что известно как строить формулы Ньютона-Котесса
на двух леммах
■ Если
![]() узлы
квадратурной формулы, точной для всех
многочленов степени
,
то
узлы
квадратурной формулы, точной для всех
многочленов степени
,
то
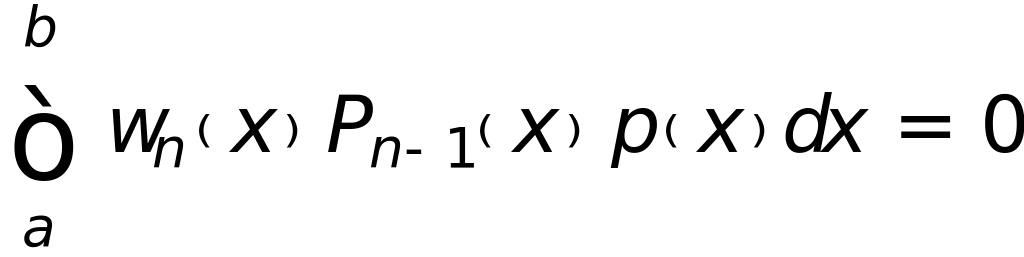
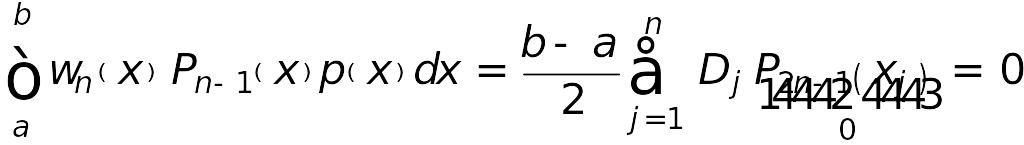
где
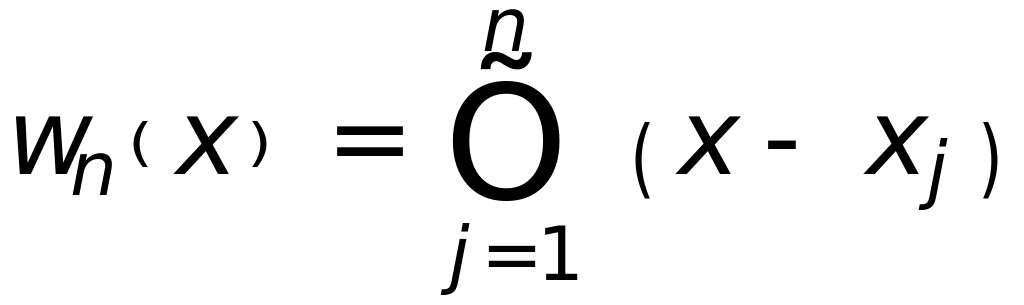 ,
,
![]() - произвольный полином, степени не выше
- произвольный полином, степени не выше
![]()
Соотношение можно использовать как
определение ортогонального полинома.
Весовая функция
![]() определяет его тип и распределение
корней на
определяет его тип и распределение
корней на
■ Пусть нули ортогонального полинома являются узлами квадратурной формулы, точной для полиномов степени (формулы Ньютона-Котесса). Тогда эта формула точна для полиномов степени
Погрешность интегрирования полиномов
степени
![]() есть
есть
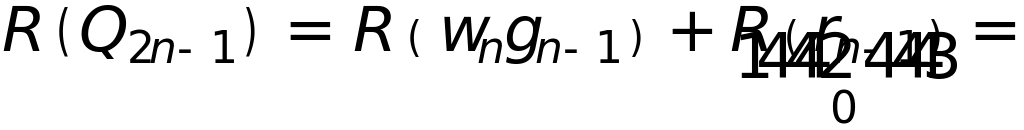
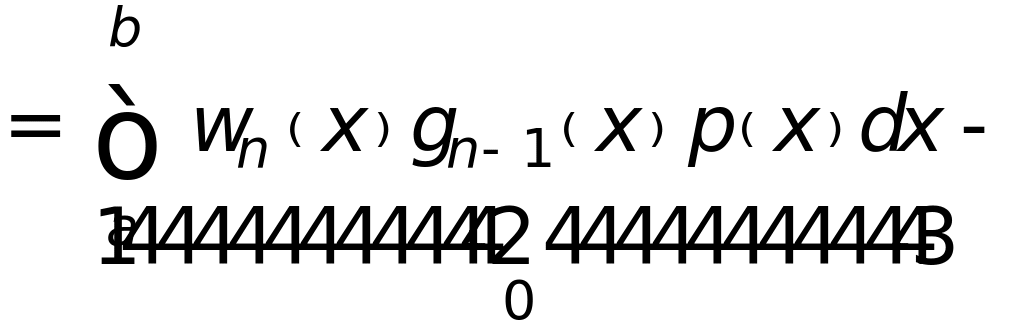 (ортогональность)
(ортогональность)
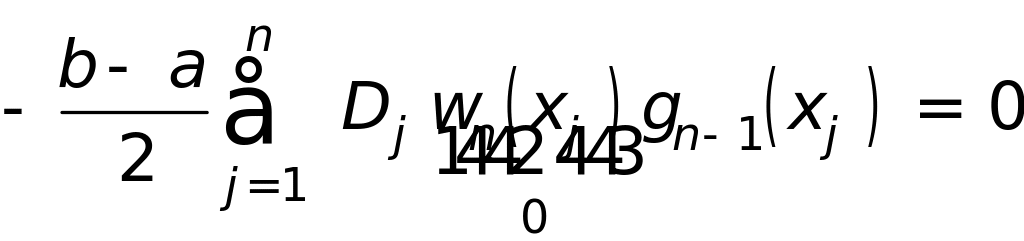 (нуль полинома)
(нуль полинома)
Трудность при построении кв.формул Гаусса заключается в нахождении корней ортогональных полиномов
Достоинства по сравнению с кв.ф-лами Ньютона-Котесса
Точны для полиномов , а не
Все квадратурные коэффициенты положительны
Можно вычислять несобственные интегралы
Наиболее употребительные ортогональные полиномы, используемые для построения квадратурных формул
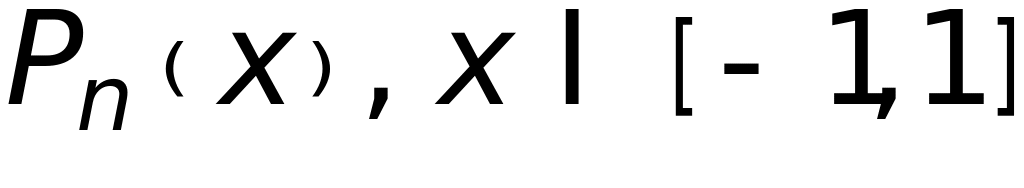 - полиномы
Лежандра
- полиномы
Лежандра
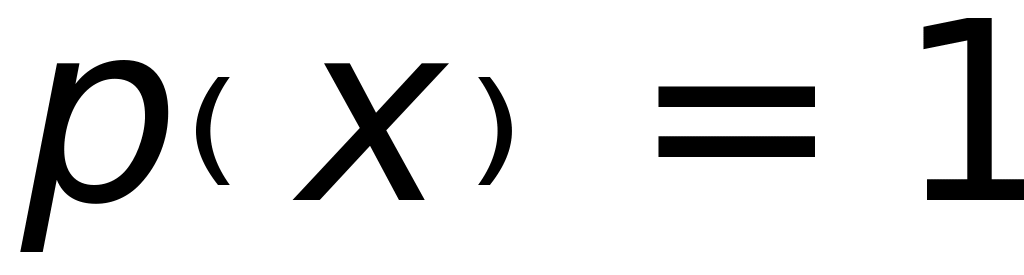
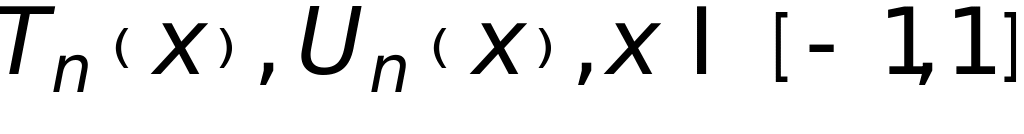 - полиномы
Чебышева I
и II
рода
- полиномы
Чебышева I
и II
рода
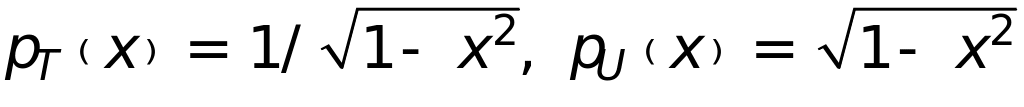
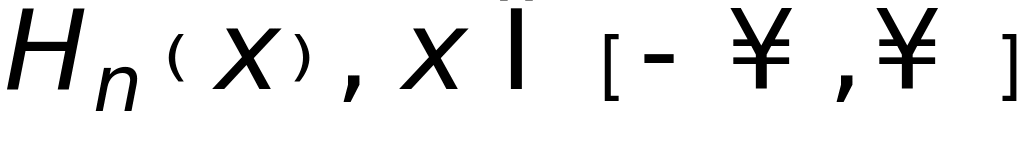 - многочлены
Эрмита
- многочлены
Эрмита
![]()
3 Решение слау
Решение СЛАУ с предварительной факторизацией матрицы, используя неортогональные преобразования. Итерационное уточнение решения СЛАУ
СЛАУ
![]()
используя неортогональные (![]() )
неособенные (
)
неособенные (![]() )
матрицы, преобразуется к виду
)
матрицы, преобразуется к виду
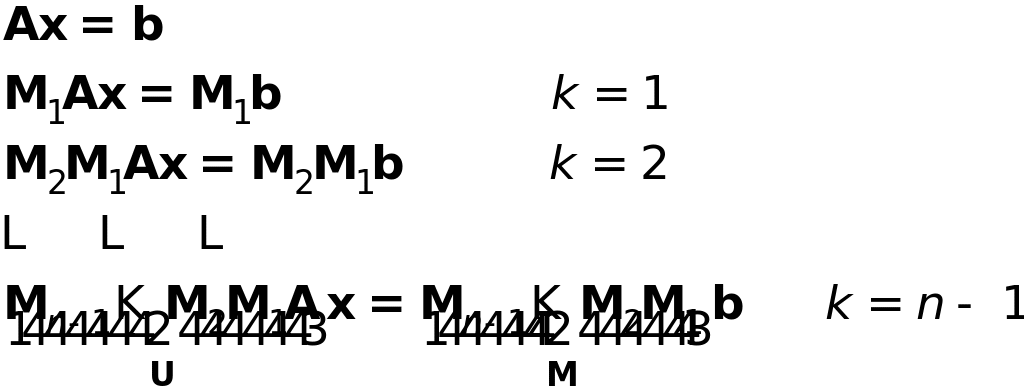
или
![]()
где
![]() - верхнетреугольная по построению,
- верхнетреугольная по построению,
![]() - неособенная нижнетреугольная.
- неособенная нижнетреугольная.
Домножая на
![]() ,
получаем вместо СЛАУ, в которой матрица
,
получаем вместо СЛАУ, в которой матрица
![]() заменена произведением двух треугольных
заменена произведением двух треугольных
![]()
Процесс факторизации матрицы можно выполнить независимо от правой части.
Решение исходной СЛАУ
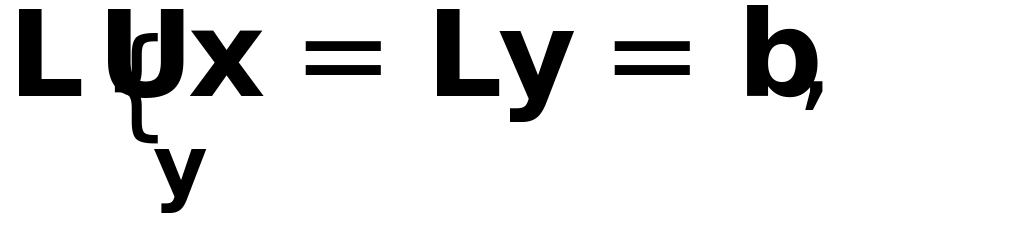 сводится
к решению двух более простых задач
сводится
к решению двух более простых задач
![]() - прямой ход в схеме Гаусса
- прямой ход в схеме Гаусса
![]() - обратный ход
- обратный ход
Для повышения устойчивости вводятся перестановки, которые
не изменяют структуру треугольных матриц
позволяют получить все элементы матриц
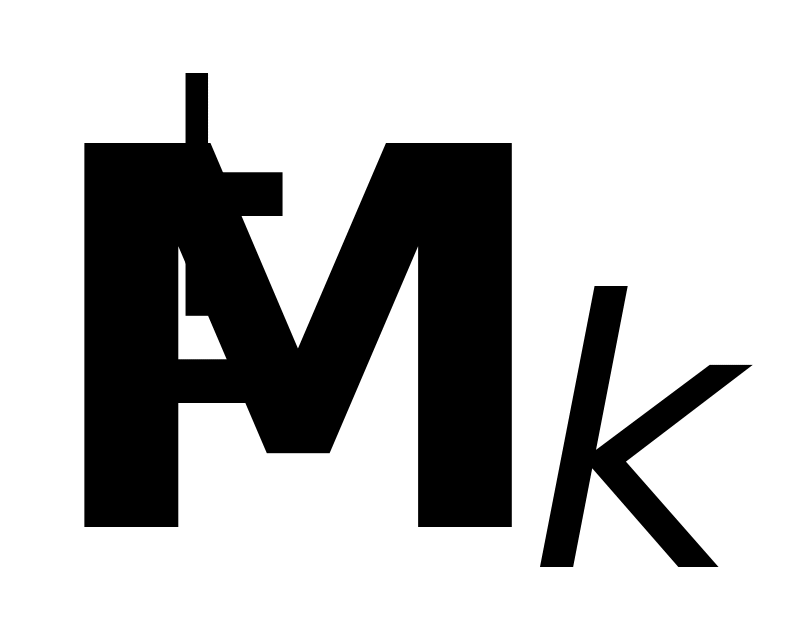 ,
по модулю не превышающих 1
,
по модулю не превышающих 1
![]()
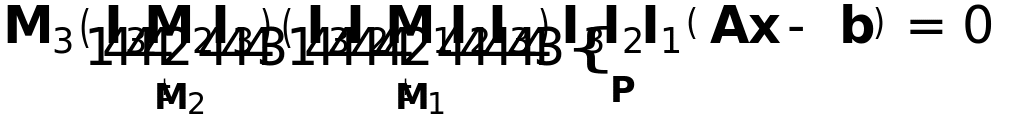
Факторизация с перестановками отличается
от наличием матрицы перестановок
![]()
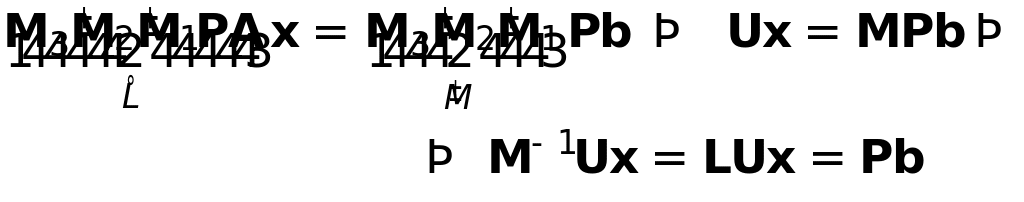
в результате чего двухшаговый процесс решения СЛАУ будет иметь вид
![]() - прямой ход в схеме Гаусса
- прямой ход в схеме Гаусса
- обратный ход
Вычисление определителей
В силу
![]()
определитель факторизованной матрицы
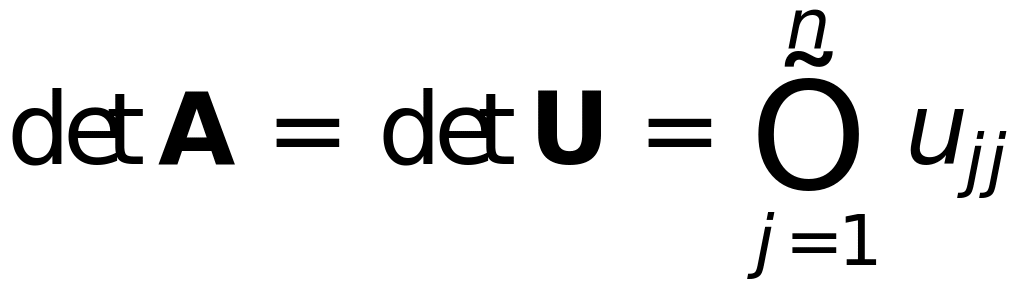
Для того, чтобы избежать переполнения или исчезновение порядка
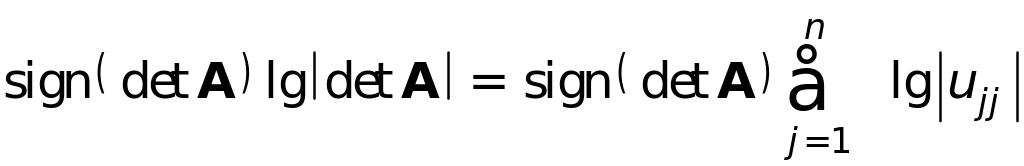
Вычисление обратной матрицы
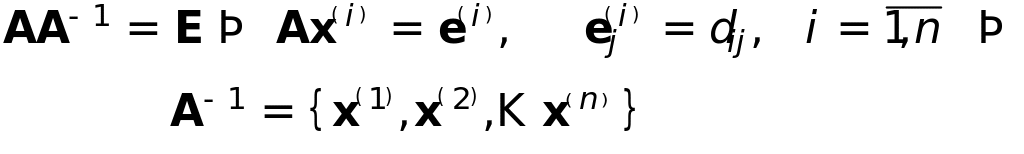
откуда наиболее экономно
![]()
Часто при вычислении обратной матрицы используется алгоритм итерационного уточнения
