
Итерационное уточнение решения слау
◙ Алгоритм
Факторизовать матрицу
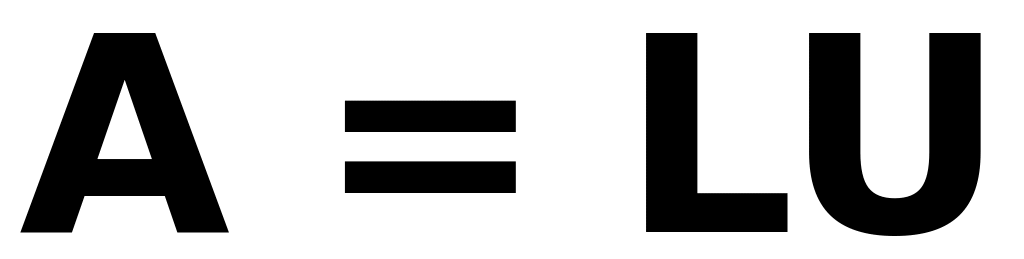 с обычной точностью
с обычной точностьюРешить СЛАУ
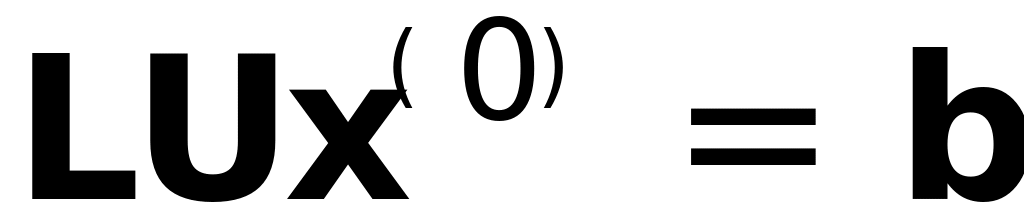 с обычной точностью
с обычной точностьюВычислить для
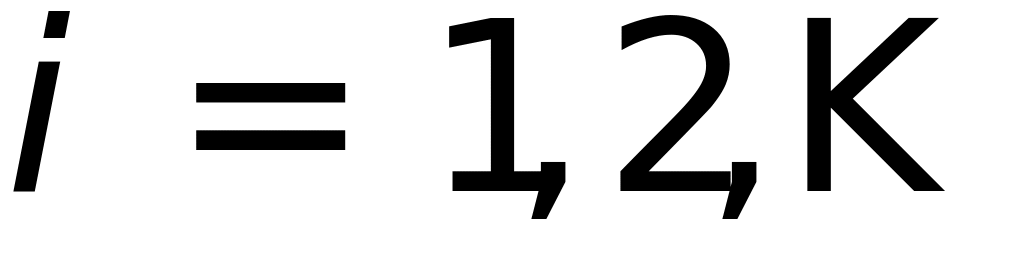 до требуемого уточнения
до требуемого уточнения
невязку
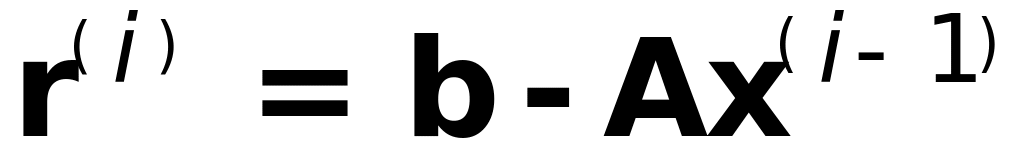 с
повышенной точностью
с
повышенной точностьюрешить СЛАУ
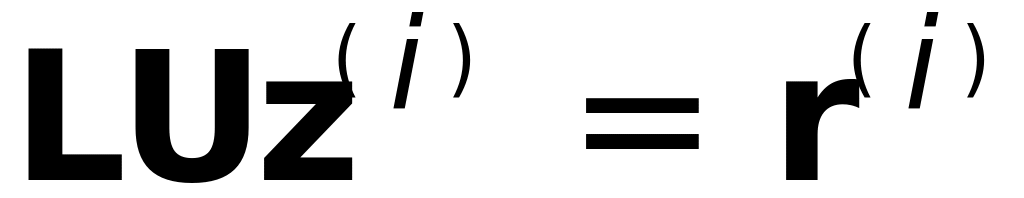 с обычной точностью
с обычной точностьюуточнить решение
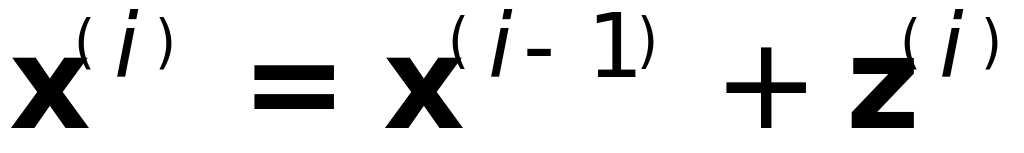 с обыч. точностью
с обыч. точностью
Качественное обоснование

4 Дифференциальные уравнения Задача Коши для оду
Одношаговые методы решения задачи Коши для ОДУ. Сходимость одношаговых методов.
Одношаговые
методы характеризуется
тем, задача Коши на интервале
![]()
![]()
решается последовательным применением
одной и той же (шаговой)
процедуры на подынтервалах
![]() ,
причем для каждого нового подынтервала
используется только одно (последнее)
из ранее найденных значений.
,
причем для каждого нового подынтервала
используется только одно (последнее)
из ранее найденных значений.
Наиболее часто используемым одношаговым методом является метод Рунге-Кутта, основанный на построении формулы приближенного интегрирования для вычисления приращения искомой функции на одном шаге
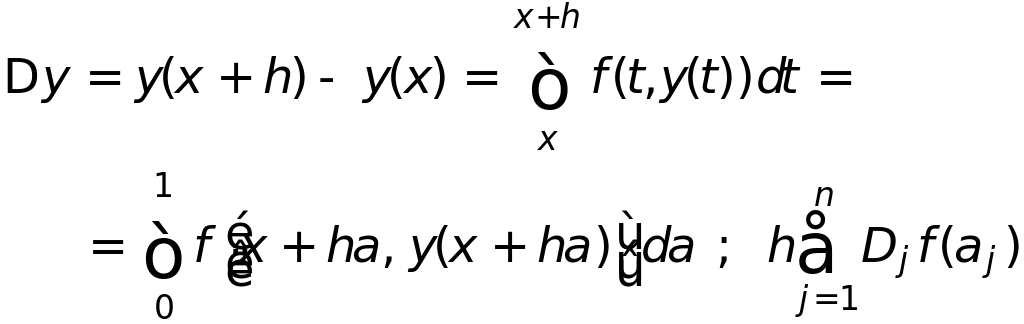
где
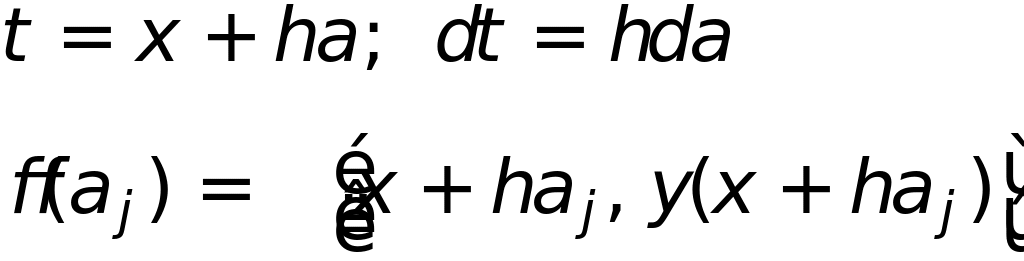
Если аналогична кв.ф-ле Ньютона-Котесса,
то
![]() - есть к-во узлов, и точность приближенного
интегрирования должна расти при
увеличении
.
- есть к-во узлов, и точность приближенного
интегрирования должна расти при
увеличении
.
В отличие от стандартных кв.ф-л, в подынтегральная функция не может быть вычислена непосредственно.
Введем
три набора параметров
![]()
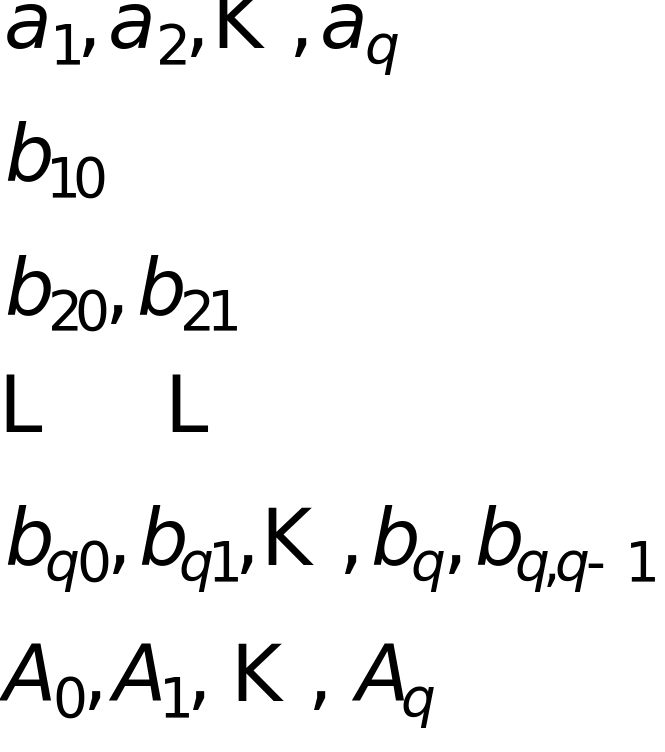
Для построения правила интегрирования вводятся параметризованные функции
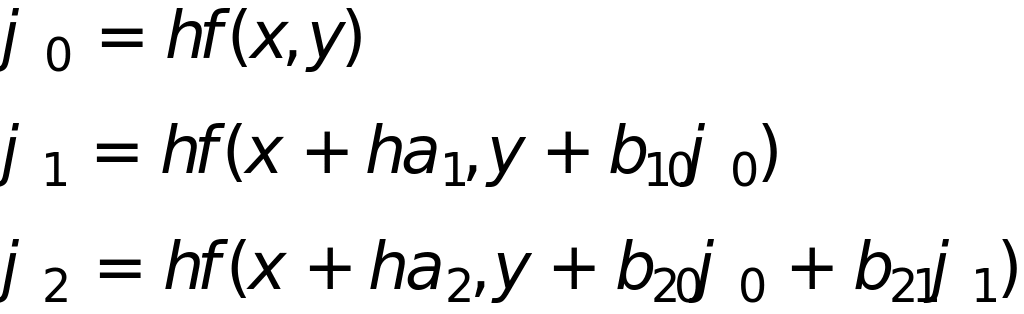
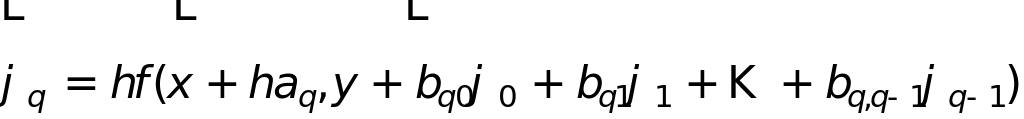
подбирают параметры так, чтобы в сумме можно было заменить
![]()
и рассматривать как квадратурную сумму
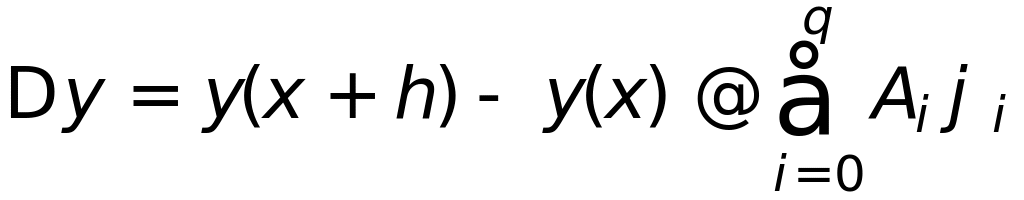
Подбор параметров выполняют так, чтобы
локальная
погрешность вычисления
![]() по правилу была минимальной
для заданного к-ва членов суммы
по правилу была минимальной
для заданного к-ва членов суммы
![]()
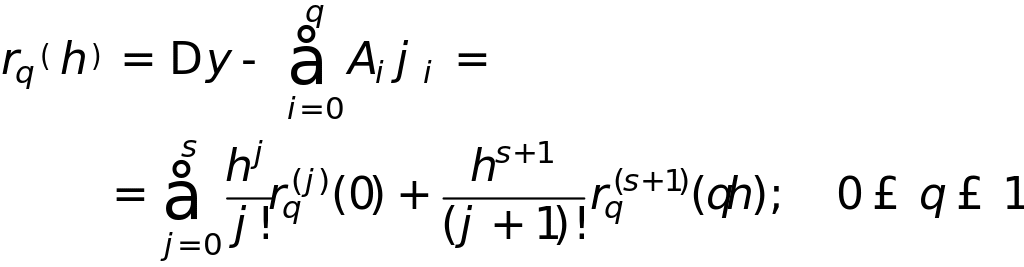
т.е. чтобы выполнялось равенство
![]()
для возможно более высокого , которое называют порядком метода
Обычно такая процедура выбора приводит к недоопределенным системам уравнений и позволяет некоторые параметры задать произвольно. Таким образом получают параметрическое семейство формул одного порядка.
Простейшими формулами Р-К являются
формула Эйлера – метод первого порядка
![]()
с локальной погрешностью
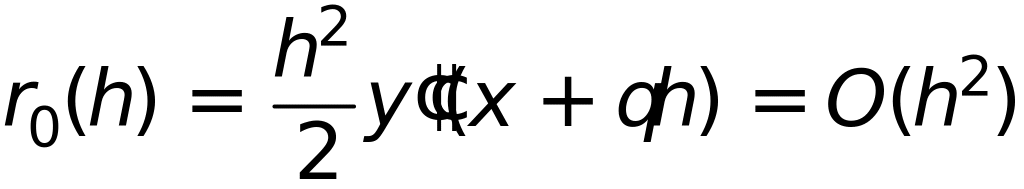
метод второго порядка с параметрами определяемыми из сисстемы уравнений
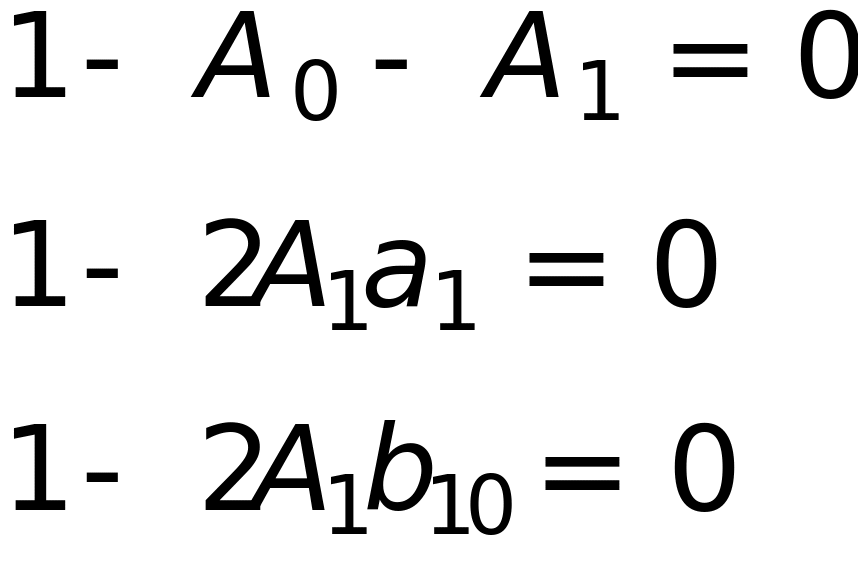
Выбирая произвольно, например,
![]() получим следующее шаговое правило
получим следующее шаговое правило
![]()
![]()
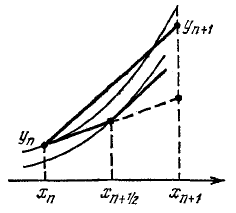
Наиболее употребителны методы четвертого порядка.
Метод р-к с контролем погрешности на шаге
Способ определения априорной погрешности на шаге в виде удобен для вычисления апостериорной оценки погрешности (оценки Рунге) и уменьшению погрешности методом Ромберга
Метод
двойного просчета по формуле порядка
,
используя шаги
![]() и
и
![]()
1) Выполним расчет значения в точке
![]() ,
используя шаг
,
используя шаг
, исходя из известного (можно считать точного) решения в
точке
![]()
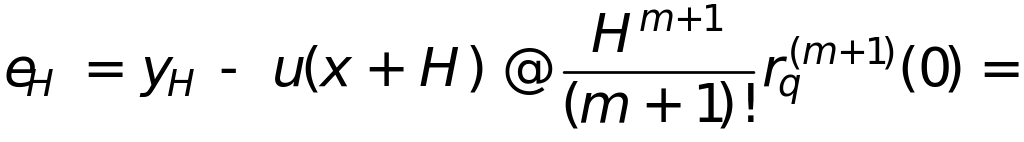
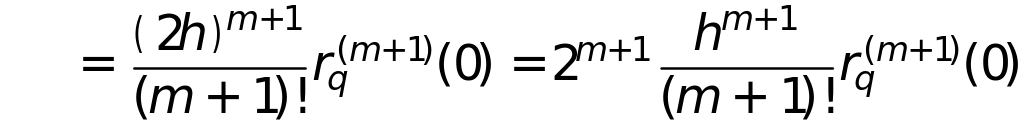
2) Выполним расчет значения в точке
,
используя дважды шаг
![]() ,
,
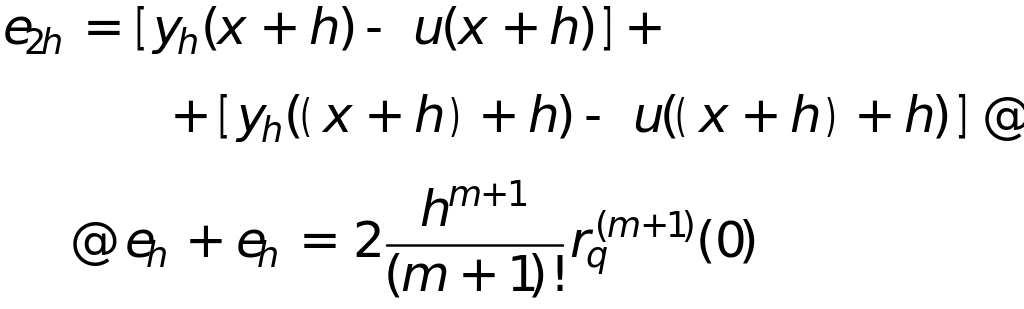
или
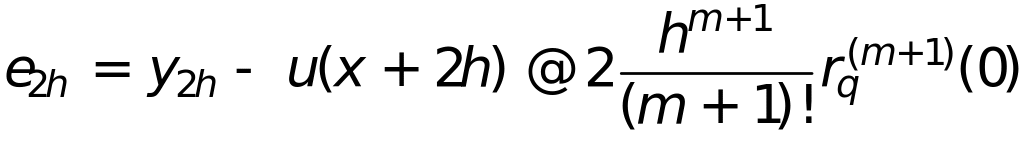
разность -
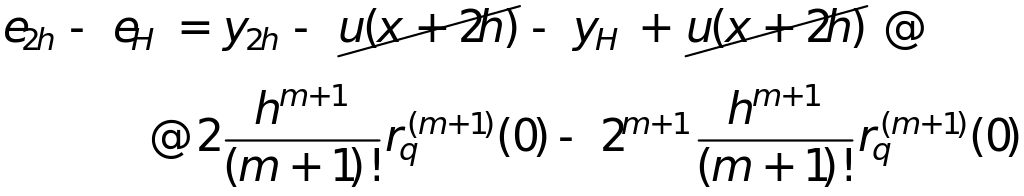
откуда
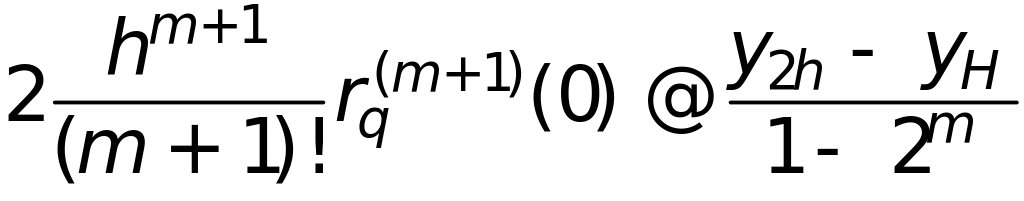
и подставляя в получаем апостериорную оценку погрешности по Рунге
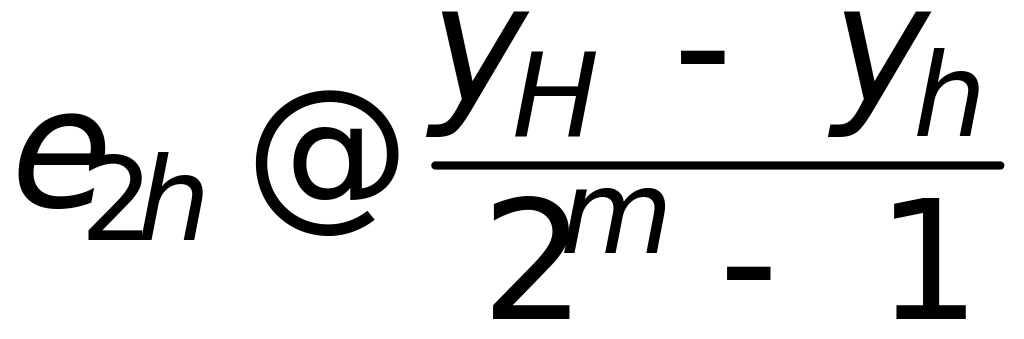
Если в разложении с учетом погрешность представить в виде
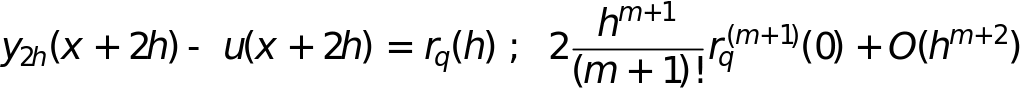 и
учесть, что вычислено приближенное
значение , то
и
учесть, что вычислено приближенное
значение , то
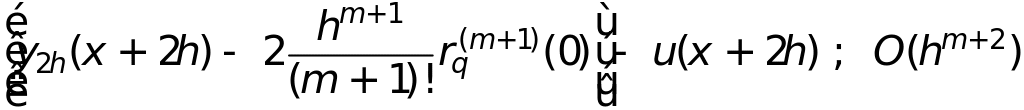
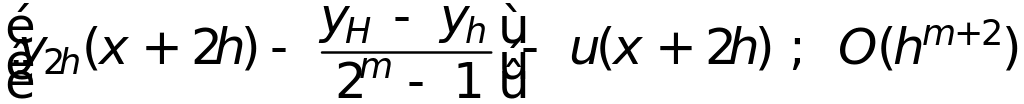
то получим уточненное значение с поправкой по Ромбергу
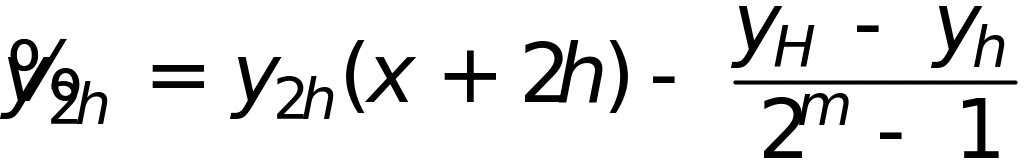
вычисленое с локальной погрешностью
![]()
как если бы использовался метод на единицу по порядку выше, чем исходное правило интегрирования.
