13

МИНИСТЕРСТВО ТРАНСПОРТА И СВЯЗИ УКРАИНЫ

^{_______________________________}

ОДЕССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СВЯЗИ им. А.С. ПОПОВА

Кафедра теории электрической связи им. А.Г. Зюко

Методические указания к выполнению лабораторных работ по дисциплине

“ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ”

для модуля № 4

Кодирование в телекоммуникационных системах

Одесса 2004

Содержание

ЛР 4.1,а Изучение кодирования и декодирования кодами Хэмминга

ЛР 4.1,б Изучение кодирования и декодирование циклическими кодами

Лабораторная работа 2.6,а ИЗУЧЕНИЕ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЕ КОДАМИ ХЭММИНГА

1 Цель работы

1.1 Изучение структуры кодека систематического кода Хэмминга (7, 4).

1.2 Исследование корректирующей способности кода (7, 4).

2 Ключевые положения

2.1 Систематическими называются корректирующие коды, кодовые комбинации которых содержат k информационных и r = n – k дополнительных символов, являющихся линейной комбинацией информационных. Обозначаются систематические коды как (n, k) либо (n, k, d). В данной работе изучаются коды (7, 4) или (7, 4, 3).

2.2 Корректирующие коды с кодовым расстоянием d = 3, позволяющие при декодировании исправлять однократные ошибки, называют кодами Хэмминга [1, с. 149]. Установим связь между параметрами n и k корректирующего кода. Известно, что для любого натурального числа r существует код Хэмминга длины n = 2^r – 1 или k + r = 2^r – 1 [1, с. 149]. Естественно, что эти равенства можно использовать и в виде неравенств k  2^r – r – 1. Последнее соотношение позволяет выбрать n и r при заданном k.

2.3 Матричный способ описания процессов кодирования и декодирования линейных блоковых кодов является наиболее удобным [1, с. 144 …149]. Так, кодирование систематическим кодом (n, k), состоящее во введении в кодовые комбинации дополнительных символов, описываются матричным соотношением

A G = B, (6,а.1)

где A = (b₁ b₂ … b_k) – матрица-строка размером k, соответствующая комбинации простого кода;

B = (b₁ b₂ … b_k b_k+1 … b_n) – матрица-строка размером n, соответствующая комбинации корректирующего кода

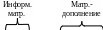
G = – (6,а.2)

порождающая (производящая) матрица размером k  n, элементы которой g_ij принимают значения 1 или 0. Порождающую матрицу можно рассматривать как объединение единичной матрицы порядка k (информационной матрицы) и матрицы-дополнения размером k  r.

Из уравнения (6,а.1) следует, что дополнительные символы связаны с информационными символами соотношением

і = k+1, k+2,…, n . (6,а.3)

Здесь сложение производится по модулю 2. Таким образом, элементы і-го столбца порождающей матрицы определяют і-ый дополнительный символ.

Строки матрицы G должны удовлетворять следующим условиям 2, с.86…88.

1. Расстояние между любыми двумя строками не должно быть меньше d.

2. Каждая строка должна содержать не менее d единиц.

3. Все строки должны быть линейно независимы, т.е. ни одна из строк не может быть получена путем суммирования ( по модулю 2) каких-либо других.

Последнее условие для матрицы (6,а.2) выполняется благодаря тому, что первые k столбцов образуют единичную матрицу. Следовательно, при построении матрицы-дополнения необходимо удовлетворить условия 1 и 2.

2.4 Если кодовое расстояние d = 3, то условия 1 и 2 для строк матрицы-дополнения можно сформулировать так.

1 Расстояние между любой парой строк должно быть не меньше 1 (т.е. достаточно, чтобы строки были несовпадающими.).

2 Каждая строка должна содержать не менее двух единиц.

Поскольку эти условия легко выполнимы, то и порождающая матрица рассматриваемого кода (n, k) может быть легко построена .