Некоторые свойства алгоритма бпф с основанием 2 и прореживанием по времени

Анализ графа на фиг. 6.3 и процедуры последовательного со­кращения вдвое размеров преобразований показывает, что на каждом этапе БПФ (т. е. при каждом сокращении размеров ДПФ) необходимо выполнить N/2 комплексных умножений. Поскольку общее количество этапов равно log₂N, то число комплексных ум­ножений, необходимое для нахождения N-точечного ДПФ, при­близительно равно N/2*log₂N. Слово приблизительно использовано по той причине, что умножения на в действительности сводятся просто к сложениям и вычитаниям комплексных чисел. Так, например, на фиг. 6.3 первый этап БПФ содержит только сложения и вычитания комплексных чисел. Даже на втором этапе используются только сложения и вычитания ком­плексных чисел. Фактически, как следует из направленного гра­фа на фиг. 6.3, вместо ожидаемых 12 (т. е. 4*log₂8) достаточно выполнить всего два нетривиальных умножения. Однако для боль­ших значений М фактическое число нетривиальных умножений хорошо аппроксимируется выражением N/2*log₂N.

Описанный выше алгоритм был назван алгоритмом с прорежи­ванием по времени, поскольку на каждом этапе входная (т. е. вре­менная) последовательность разделяется на две обрабатываемые последовательности меньшей длины, т. е. входная последователь­ность прореживается на каждом этапе. Другая форма алгоритма БПФ (с прореживанием по частоте) будет описана ниже, а сейчас целесообразно обсудить некоторые общие свойства алгоритмов БПФ.

Базовая операция алгоритма с прореживанием по времени (так называемая „бабочка") состоит в том, что два входных числа А и В объединяются для получения двух выходных чисел Х и Y следующим образом:

(6.14)

На фиг. 6.4 изображен направленный граф базовой операции (6.14). Внимательное рассмотрение направленного графа на фиг. 6.3 показывает, что каждый из этапов содержит N/2 базовых операций.

Фиг. 6.4. Базовая операция алгоритма БПФ.

В случае когда множитель — нетривиальный, для каждой базовой операции необходимо выполнить только одно умножение, поскольку величинуBможно вычислить и запом­нить. Таким образом, структура базовых операций такова, что для выполнения БПФN-точечной последовательности, размещен­ной в памяти, достаточно иметь лишь одну дополнительную ячей­ку памяти. Результаты всех промежуточных этапов БПФ можно размещать в те же ячейки памяти, где находились исходные дан­ные. Поэтому для хранения и входной, и выходной последователь­ностей можно использовать один и тот же массив ячеек памяти. Алгоритм, в котором для размещения входной и выходной после­довательностей используются одни и те же ячейки памяти, назы­вается алгоритмом БПФ с замещением.

На фиг. 6.5 алгоритм БПФ с основанием 2 иллюстрируется не­сколько иначе.

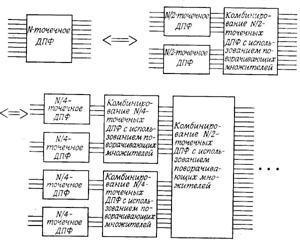
Фиг. 6.5. Типичное разложение для алгоритмов БПФ с основанием 2.

Все ДПФ являются двухточечными и не требуют операций умножения. Однако при объединении двух (N/2)-точеч­ных ДПФ в одно N-точечное ДПФ приходится выполнять около N/2 умножений. Из примера на фиг. 6.3 видно, что N-точечное БПФ состоит из log₂N этапов, причем все операции умножения используются только при объединении результатов ДПФ. По­скольку эти умножения используются во всех алгоритмах БПФ, соответствующие множители получили специальное название поворачивающих множителей (иногда их называют фазовыми множи­телями или множителями вращения).