2.Почленное дифференцирование
Теорема
(для рядов): Пусть
для любого
существует производная
,
пусть
равномерно сх-ся на Х к
,и
пусть сущ.
,
тогда
,
.
Теорема
(для последовательностей): Пусть
для любого
существует производная
,
пусть
равномерно сх-ся на Х к
,и
пусть существует
,
тогда
,
.
24. Тригонометрический ряд фурье
Опр.1
Ряд вида
(1) называется тригонометрическим
рядом.Его
частичные суммы явл-ся лин. комбинациями
ф-й, входящих в систему
cos x, sin x, cos 2x, sin 2x, …, cos nx, sin nx, … . (2)
Опр.2 Множество ф-ий (2) наз-ся тригонометрической системой.
Лемма 1. Тригонометрическая система (2) обладает свойствами:
ортогональность, т.е. интеграл по отрезку [-π, π] от произведения двух
различных функций, входящих в нее, равен нулю
(3)
2)
(4)
Теорема
1. Пусть
(5) и ряд, стоящий в правой части этого
равенства, сходится равномерно на
отрезке [-π,
π].
Тогда
, 
,
n=1,2,
… . (6)
Опр.3 Пусть функция f абсолютно интегрируема на отрезке [-π, π]. Тригонометрический ряд (1), коэффициенты которого задаются формулами (6), называется тригонометрическим рядом Фурье, а числа an и bn – коэффициентами Фурье функции f.
Теорему 1 в этих терминах можно перефразировать следующим образом:
всякий равномерно сходящийся тригонометрический ряд является рядом Фурье своей суммы.
Разложение функции в тригонометрический ряд Фурье единственно
Функция
,
называется
кусочно-гладкой на
,
если как сама функция
,
так и ее производная функция
непрерывны
или кусочно-непрерывны на
.
ТЕОРЕМА (о достаточных условиях сходимости ТРФ)
Если
–периодическая
функция
кусочно-гладкая
на
,
то
1) ТРФ функции
существует; 2) ТРФ сходится всюду;
3)
сумма ТРФ равна
в
каждой точке непрерывности функции
и
равна числу
–
(полусумме значений лево- и правостороннего
пределов функции
)
в каждой ее точке разрыва.
25. Кратні інтеграли (подвійні, потрійні): означення властивості, обчислення, застосування.
Пусть в n-мерном пр-ве Rn задана ограниченная область Ω с кусочно-гладкой границей Г (Ω`=Ω+Г) и на Ω (или Ω`) задана ф-я f(x)=f(x1, …, xn).
наз. мерой мн-ва Ω, а само мн-во Ω наз-ся
измеримым.
Разрежем Ω` на части Ωj,
пересекающиеся разве что по своим
границам, которые будем считать
кусочно-гладкими. Для краткости будем
говорить, что мы произвели разбиение ρ
мн-ва Ω (сп-б разбиения не имеет знач-я).
Введем понятие диаметра множества Ω –
это есть точная верхняя грань
.
Выберем в каждой части Ωj
по произвольной точке ξj=(ξj1.
…, ξjn
) (ξj
Ωj) и составим сумму
,
которую будем наз-ть интегральной
суммой Римана ф-и f,
отвечающей разбиению ρ.
Предел суммы
,
когда максимальный диаметр частичных множеств Ωj стремится к нулю, называется кратным интегралом от функции f на Ω (или по Ω`).
Рассмотрим трехмерное пр-во R3,
в котором определена прямоугольная
система координат (x,
y, z).
В нем задана непрерывная поверхность
z=f(x,
y), (x,
y)
Ω,
где Ω – огр. двумерное мн-во, для кот-го
возможно опр-ть понятие его площади
(двумерной меры). В качестве Ω может быть
взят круг, прямоугольник, эллипс и т. д.
Ставится задача: опр-ть объем тела,
ограниченного сверху поверхностью
z=f(x,
y), снизу плоскостью
z=0 и с боков цилиндрической
поверхностью, проходящей через границу
Г плоского множества Ω, с образующей,
параллельной оси z. Решая
задачу о нахождении объема, проводим
рассуждения, аналогичные приведенным
выше для n-мерного случая.
Приходим в результате к определенному
двойному интегралу (Римана):
.
Пусть теперь в трехмерном пр-ве R3, где определена прямоугольная система координат (x, y, z), задано тело Ω (мн-во) с неравномерно распределенной в нем массой и плотностью распределения m(x, y, z) тела Ω. Решая эту задачу, приходим к определенному тройному интегралу (Римана)
Свойства кратных интегралов:
Св.1:
(Линейность).
,
кроме того
.
Св.2:
.
Св.3: (Аддитивность
интеграла). Пусть
и
- допустимое множества, тога выполняются
следующие импликации:
.
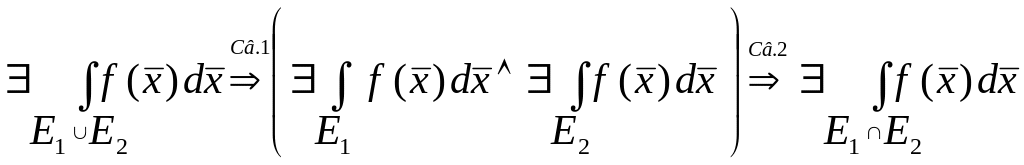Кроме того
.
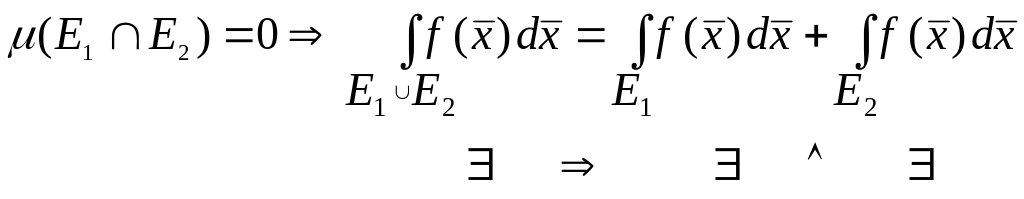Св.4:
.
Св.5:
.
Св.6:
.
Св.7:
.
Св.8:
.
Св.9: (Обобщённая Th(ма) о среднем)
Св.10: (Непрерывный случай Th(мы) о среднем).
Св.11: (Непрерывный случай обобщённой Th(мы) о среднем).
.
Св.12:
.