1.----------------------------------------------------------------------------------------------------------------

Прямоугольная таблица m×n чисел, расположенных в m строках и n столбцах  называется

      прямоугольной (m, n) матрицей или просто матрицей.

      Числа m и n называются порядками или размером матрицы.

      Для обозначения матриц используют квадратные скобки [... ], две вертикальные

      черты ‌ ‌ ... ‌ ‌ или, чаще, круглые скобки (...):

      

       Числа a_{i j} называют элементами матрицы. Иногда матрицу записывают в виде A = {a_{i j}}_mn.

        Две матрицы называются равными, если они имеют одинаковые размеры и равные                              соответственные  элементы:

      A = {a_{i j}}_mn, B = {b_{i j}}_mn, A = B, если m = n, a_{i j} = b_{i j} , i = 1, 2, ..., m, j = 1, 2, ..., n.

  Квадратная матрица A размера 3×3, матрица имеет 3 строки и 3 столбца:

        Элементы матрицы:

a₁₁= 1, a₁₂= 2, a₁₃= 3, a₂₁= 7, a₂₂= −2, a₂₃= 9, a₃₁= 50, a₃₂= −12, a₃₃= 0,

        главную диагональ образуют элементы

a₁₁= 1, a₂₂= −2, a₃₃= 0.

Линейными операциями называются операции сложения матриц и умножение матрицы на число.

    Суммой двух матриц одинаковой размерности  называется матрица той же размерности, каждый

элемент которой равен сумме соответствующих элементов слагаемых:

.

,

     Произведением матрицы на число называется матрица той же размерности, каждый элемент которой

     равен произведению  соответствующего элемента на число:

.

Сумма двух прямоугольных матриц:

    

        Произведение матрицы на число:       

 

2.---------------------------------------------------------------------------------------------------------------------------------

Определитель матрицы

Для любой квадратной матрицы может быть найдена величина, называемая определителем.

Определитель — это квадратная таблица чисел или матиматических символов (Δd).

Для матрицы второго порядка определитель вычисляется по формуле:

Разложение по строке или столбцу

Формулы разложения по строке или столбцу:

Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу.

В этих формулах - алгебраические дополнения элементов а_ij матрицы А, где M_ij — миноры элементов а_ij матрицы А.

Минором M_ij элемента а_ij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент a_ij/

Правило Саррюса

Дописывание двух первых строк или столбцов.

В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33

Пример 32.2

Вычислить определитель двумя способами: с помощью разложения по первой строке и по правилу треугольника:

Решение:

Свойства определителей

Свойство (1) Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.

Свойство (2) При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.

Свойство (3) Определитель равен нулю, если он имеет две равные строки (столбца).

Свойство (4) Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.

Свойство (5) Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится.

Следствие из свойств 32.4 и 32.5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.

Свойство (6) Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю.

Пример 32.3

Вычислить определитель, используя свойства:

Решение:

1. Третью строку умножим на подходящие множители и прибавим к остальным:

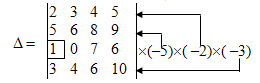
получим:

Метод Крамера

Решение систем уравнений

Пусть имеется система уравнений:

Обозначим через Δ определитель матрицы системы и через Δ_j определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,...n).

Теорема 1

Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле:

Нахождение обратной матрицы

Путь имеется матрица:

Матрица:

называется присоединенной для матрицы А. Здесь А_ij алгебраическое дополнение элементов а_ij матрицы А

3.-------------------------------------------------------------------------------------------------------------------------

Рациональные числа

 

Отрицательные числа. Целые отрицательные числа.

Дробные отрицательные числа. Положительные числа.

Рациональные числа.

 

Отрицательные числа появляются, когда из меньшего числа вычитают большее, например:

 

10 – 15 = – 5 .

 

Знак «минус» перед 5 показывает, что это число отрицательное.

Ряд целых отрицательных чисел бесконечен:

 

–1,  –2,  –3,  – 4,  –5, ...

Целые числа - это натуральные числа, целые отрицательные числа и ноль:

 

... , –3,  –2,  –1,  0,  1,  2,  3, ...

 

Дробные отрицательные числа появляются, например, когда из меньшего дробного числа вычитают большее:

Можно также сказать, что дробные отрицательные числа появляются в результате деления целого отрицательного числа на натуральное:

Положительные числа ( целые и дробные ) в противоположность отрицательным числам ( целым и дробным ) рассматриваются в арифметике.

 

Рациональные числа – это положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее:

 

Число называется рациональным, если оно может быть представлено в виде обыкновенной несократимой дроби вида: m / n , где  m  и  n  целые числа.

Вещественные или действительные числа — математическая абстракция, служащая в частности для представления физических величин. Такое число может быть интуитивно представлено как отношение двух величин одной размерности, или описывающие положение точек на прямой. Множество вещественных чисел обозначается и часто называется вещественной или числовой прямой. Формально вещественные числа строятся на базисе более простых объектов таких, как целые и рациональные числа. Свойства вещественных чисел являются важнейшим объектом изучения математического анализа.

Содержание

[показать]

Аксиоматическое определение Править

Полное упорядоченное поле Править

Пусть на множестве X заданы две бинарные операции + и и отношение порядка . Четвёрка называется полным упо95.58.234.195 13:55, декабря 7, 2011 (UTC)рядоченным полем, если

1. представляет собой алгебраическое

4. поле;

5. является полностью упорядоченным множество с отношением порядка , то есть

   • порядок устойчив относительно сложения:

• порядок устойчив относительно умножения:

.

6. упорядоченное множество удовлетворяет принципу полноты Вейерштрасса, то есть любое ограничен

Изоморфизм полных упорядоченных полей Править

Пусть даны два полных упорядоченных поля и . Тогда они называются изоморфными, если существует биекция такая, что

1. 

2. 

3. f(0_X) = 0_Y;

4. f(1_X) = 1_Y;

5. 

Любые два полных упорядоченных поля изоморфны между собой. Таким образом с точностью до свойств операций и порядка существует только одно полное упорядоченное поле. Оно называется полем действительных чисел. Аксиомы полного упорядоченного поля, перечисленные выше, называются аксиомами вещественных чисел.

Пополнение рациональных чисел Править

Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике . Рассмотрим семейство фундаментальных последовательностей рациональных чисел Назовём две последовательности {r_n} и {q_n} эквивалентными, если существует предел

Введённое таким образом отношение является отношением эквивалентности и следовательно разбивает рассматриваемое семейство на непересекающиеся классы эквивалентности. Отождествляя рациональное число с фундаментальной последовательностью , можно считать, что полученное фактор-множество содержит рациональные числа. Зададим на фактор-множестве бинарные операции и порядок следующим образом:

• [{r_n}] + [{q_n}] = [{r_n + q_n}];

• 

• 

Непосредственно проверяется, что это построение корректно и полученная таким образом четвёрка является полным упорядоченным полем. В силу изоморфизма полных упорядоченных полей эту структуру можно называть полем действительных чисел и более того считать, что

Дедекиндовы сечения Править

Рассмотрим опять множество рациональных чисел Дедекиндовым сечением (A,B) множества называется такое его разбиение, что A замкнуто снизу, B замкнуто сверху, и A не содержит наибольшего элемента. Отождествим произвольное рациональное число c сечением (A_q,B_q), где

и введём на семействе Дедекиндовых сечений бинарные операции и порядок следующим образом:

• (A₁,B₁) + (A₂,B₂) = (A₃,B₃), где

  • 

  • 

• , где

  • 

  • 

• 

Опять непосредственное проверяется, что таким образом построено полное упорядоченное поле, содержащее в себе с точностью до изоморфизма рациональные числа. В силу изоморфизма всех упорядоченных линейных полей между собой можно считать полученное поле вещественными числами.

Пример Править

Число соответствует сечению (A,B), где

Бесконечные десятичные дроби Править

Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.

Бесконечной десятичной дробью (со знаком) называется последовательность вида , где d_i являются десятичными цифрами, то есть .

Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где

Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.

Значение десятичной дроби формально задается суммой ряда .