1.3Смежность вершин и ребер

Пусть v₁, v₂ — вершины, e = (v₁,v₂) – соединяющее их ребро. Тогда вершина v₁ и ребро е инцидентны, вершина v₂ и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается

, ,

(Если не оговорено противное, то подразумевается и обозначается просто ).

При этом .

Если — множество вершин, то Г(А) — множество всех вершин, смежных с вершинами из А:

.

1.4Изоморфизм графов

Говорят, что два графа G₁(V₁, E₁) и G₂(V₂, E₂) изоморфны (обозначается G₁~G₂), если существует биекция h: , сохраняющая смежность:

Изоморфизм графов есть отношение эквивалентности. Действительно, изомор­физм обладает всеми необходимыми свойствами:

1. рефлексивность: G~G, где требуемая биекция суть тождественная функция;

2. симметричность: если G₁~G₂ с биекцией h, то G₂~G₁ с биекцией h^-1;

3. транзитивность: если G₁~G₂ с биекцией h и G₂~G₃ с биекцией g, то G₁~G₃ с биекцией .

Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.

Пример. Три внешне различные диаграммы, приведенные на рис. 3, являются диаграм­мами одного и того же графа K_3,3.

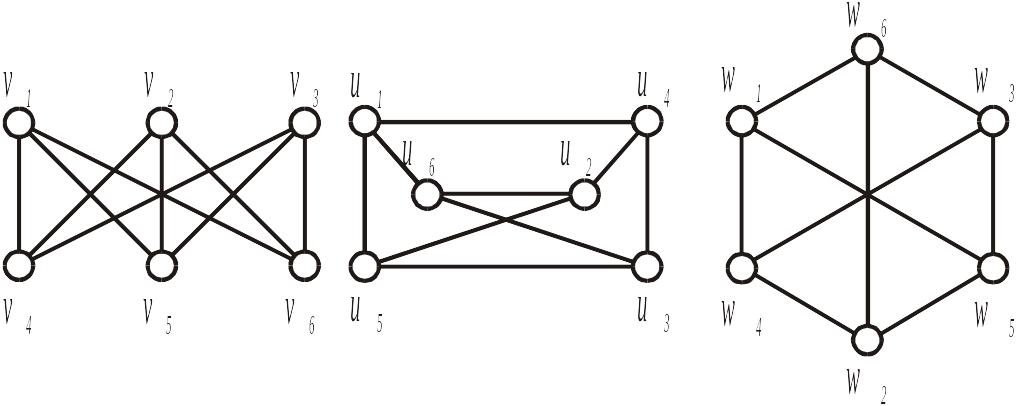
Рис. 3. Диаграммы изоморфных графов

Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) — инварианты графа G.

Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.

Пример. Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф. На рис. 4 представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны.

Рис. 4. Диаграммы неизоморфных графов с совпадающими инвариантами

1.5Способы задания графов

Графы можно задать различными способами:

1. Аналитическим (представление графа в виде G = (V, E) или с помощью перечисления всех его вершин и ребер (дуг)).

2. Геометрическим (изображение графа в виде рисунка).

3. Матричным (с помощью специальных матриц).

2Элементы графов

После рассмотрения определений, относящихся к графам как к цельным объек­там, естественно дать определения различным составным элементам графов.

2.1Подграфы

Граф G'(V', Е') называется подграфом графа G(V, E) (обозначается ), если и/или .

Подраф G'(V', Е') называется остовным подграфом графа G(V, E), если , то есть остовный подграф G' содержит все вершины графа G(V, E).

Если и и , то подграф G'(V', Е') называется собственным подграфом графа G(V, E).

Подграф G'(V', E') называется правильным подграфом графа G(V, E), если G' содержит все возможные ребра G:

.

Правильный подграф G'(V', Е') графа G(V, Е) определяется подмножеством вер­шин V'.

На рис. 5 приведен пример графа G, а также варианты его остовного подграфа, собственного подграфа и правильного подграфа.

2.2Валентность вершин

Количество ребер, инцидентных вершине v, называется степенью (или валент­ностью) вершины v и обозначается d(v):

, .

Обозначим минимальную степень вершины графа G через (G), а максималь­ную — через (G):

, .

Если степени всех вершин равны k, то граф называется регулярным степени k:

При этом (G) = (G) = k.

а) граф G б) остовный подграф графа G

в) собственный подграф графа G г) правильный подграф графа G

Рис. 5. Подграфы графа G

Степень регулярности является инвариантом графа и обозначается r(G). Для нерегулярных графов r(G) не определено. На рис. 6 приведена диаграмма регулярного графа степени 3.

Рис. 6. Диаграмма регулярного графа степени 3

Если степень вершины равна 0 (то есть d(v) = 0), то вершина называется изолиро­ванной. Если степень вершины равна 1 (то есть d(v) = 1), то вершина называется концевой, или висячей.

Для орграфа число дуг, исходящих из вершины v, называется полустепенью исхо­да, а входящих - полустепенью захода. Обозначаются эти числа, соответственно, и .

Относительно введенных понятий имеет место теорема Эйлера: Сумма степеней вершин графа равна удвоенному количеству ребер:

, .