методичка по математике семестровые

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра высшей математики

Неопределенный интеграл

Задания для самостоятельной работы и методические указания

Новокузнецк

2011

УДК 517(07) Н 525

Рецензент кафедра физики Сибирского государственного индустриального уни-

верситета (зав. кафедрой д.ф.-м.н., проф. Громов В.Е.)

Н 525 Неопределенный интеграл: задания для самостоятельной работы и методические указания/ Сиб. Гос. индустр. ун-т; сост.: Л.М.Калинина –Новокузнецк: Изд. центр СибГИУ, 2011.–16 с.

Приведены варианты и образцы выполнения индивидуальных заданий по разделу «Неопределенный интеграл» дисциплины «Математика».

Предназначены для студентов всех направлений и специально-

стей.

2

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ РАБОТЫ

1. При вычислении интегралов 1 – 3 нужно использовать замену переменной или способ подведения функции под знак дифференциала и ответ проверить дифференцированием.

Пример.

ln2

x

ln x =t

2

1

3

1

3

∫

dx =

dx

= ∫t

dt =

t

+C

=

ln

x +C.

x

= dt

3

3

x

Проверка.

1

ln

3

′

=

1

3ln

2

x

1

=

ln2 x

.

x +C

3

x

x

3

Здесь использована формула замены переменной в неопределенном интеграле

∫ f (t)dt =		t =ϕ(x)		′
		′		= ∫ f [ϕ(x)] ϕ (x)dx.
		dt =ϕ (x)dx

Причем формула применена справа налево, так как выражение ϕ(x) = ln x принято за новую переменную t, а ϕ′(x)dx = dxx = dt.

Новую переменную можно не обозначать другой буквой, а подвести ее под знак дифференциала:

∫lnx2 x dx =∫ln2 x dxx = ∫ln2 x d ln x = 13 ln3 x +C.

При подведении функции под знак дифференциала часто бывает нужным сделать «поправку», чтобы относительно новый переменной интегрирования – той, что под знаком дифференциала – интеграл стал табличным.

Пример.

∫

dx

1

∫(2x +3)

−3

1

(2x +3)−2

1

=

d (2x +3) =

+C = −

+C.

(2x +3)3

2

2

−2

4(2x +3)2

Проверка.

1

′

1

−2

′

1

−3

1

−

+C

=

−

(2x +3)

+C

= −

(−2)(2x +

3)

2

=

.

4(2x +

3)

2

4

4

(2x +3)

3

При выполнении второй части задания нужно хорошо знать таблицы производных, дифференциалов и первообразных основных функций (приложение 1), тогда легко догадаться, что нужно взять за переменную интегрирования, чтобы интеграл стал табличным.

3

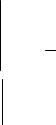
2. Для нахождения интегралов 4 и 5 используется формула интегрирования по частям ∫udv =uv −∫vdu, где u = u(x), v = v(x) -

дифференцируемые функции. Если подынтегральное выражение имеет вид xn cos ax dx, xn sin ax dx или xneax dx , то полагают u = xn , а

dv = cos axdx, dv =sin ax, dv = eax dx.	если же подынтегральное		выражение
содержит обратные функции,	т.е.	имеет вид xn arccos x dx, xn arcsin x dx
или xn ln xdx , то роли u и	dv	распределяются иначе,	а именно:

u= arccos x, u = arcsin x, u = ln x, а dv = xn dx.

3.Интегралы 6 и 7 содержат дроби. При их интегрировании нужно выделить целую часть, если дробь неправильная, знаменатель представить в в идее произведения сомножителей и разложить дробь на сумму простейших дробей, используя метод неопределенных коэффициентов. Например:

x −1

dx =

x −1

dx =

A

+

Bx +C

dx.

∫x

3

∫(x +2)(x

2

∫

2

+8

−2x +4)

(x

−2x +4)

x +2

После приведения к общему знаменателю должна получиться дробь, числитель которой равен числителю данной подынтегральной дроби

x −1 = A(x2 −2x +4) +(Bx +C)(x +2).

Дадим x значения -2 и 0 и сравним коэффициенты при x2 .

−2 −1 = A((−2)2 −2(−2) +4) +(B(−2) +C)(−2 +2); −3 =12 A; x = −2 A = −14 .

x= 0 −1 = A 4 +2C; −1 = 4 − 1 +2C; C = 0.

4

	2			1			1
x		0 = A + B, B = −A = −	−			; B =		.
				4			4

Подставляя найденные значения коэффициентов А, В и С, получим

∫	x −1		1	∫	dx		1	∫	xdx
		dx = −	4			+	4			.
	x3 +8				x +2				x2 −2x +4

Вычислим каждый интеграл отдельно.

	∫	dx	=∫d (x +2)	=ln		x +2		+C.
		x +2	x +2

4

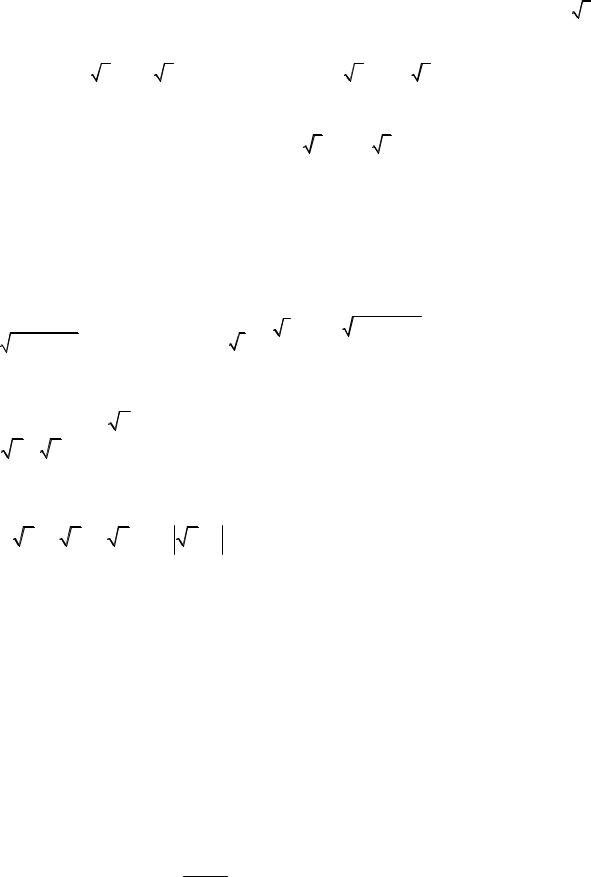
∫	xdx	=∫	xdx	=∫	xdx
	x2 −2x +4		(x2 −2x +1) +3		(x −1)2 +3

x −1 =t

= ∫

(t

+

1)dt

= ∫

tdt

+∫

dt

=

dx = dt

=

t

2

+3

t2 +3

t2

+( 3)2

x =t +1

=

1 ln(t2

+3) +

1

arctg

t

+C =

1 ln(x2

−2x +

4) +

1

arctg

x −1

+C.

3

3

3

3

2

2

∫

x −1

1

1

2

1

x −1

dx = −

4 ln

x +2

+

8 ln(x

−2x +4) +

arctg

+C.

x3 +8

4

3

3

4. Интегралы 8 и 9 содержат иррациональные функции; для вычисления используется метод замены переменной: новую переменную выбирают таким образом, чтобы интеграл сводился либо к табличному, либо к интегралу от рациональной функции.

Пример.

а)

∫

(2x +5)dx

=

x2 +5x −1 =t

= ∫

dt

= 2 t +C = 2 x2 +5x −1 +C;

2

(2x +5)dx = dt

x

+5x −1

t

б)

dx

t = 6 x, x =t6

6t5dt

t3

(t3 −1) +1

∫

=

dx = 6t5dt

=

∫

= 6∫

dt = 6∫

dt =

x − 3 x

t3 −t2

t −1

t −1

= 6

∫(t

2

+t +1)dt +∫

dt

= 6

1

t

3

+

1

t

2

+t +ln

t −1

+C =

t

−1

3

2

=2 x +33 x +6 6 x +6 ln 6 x −1 +C.

5.При вычислении интегралов от тригонометрических функций используются тригонометрические тождества и формулы:

cos2	x =1−sin2 x;				sin2 x =1−cos2 x;
cos2	x =	1	(1+cos	2x);	sin2 x =	1	(1−cos 2x);
		2				2

cosαx cos βx = 12 (cos (α +β)x +cos (α −β)x); sin αx cos βx = 12 (sin (α +β)x +sin (α −β)x); sin αx sin βx = 12 (cos (α −β)x −cos (α +β)x);

tg 2 x = cos12 x −1; cos x sin x = 12 sin 2x.

5

Примеры. а)

∫

4

∫

2

1

∫

2

dx

∫

2

tg

xdx =

tg

x

−1 dx

=

tg

x

−

tg

xdx =

2

x

cos

2

x

cos

∫

2

∫

1

1

3

=

tg

x d (tgx) −

−

1 dx =

tg

x −tgx + x +C.

2

x

3

б)

cos

x

x

x

x

x

∫

3

dx

∫

2

dx

∫

2

dx

cos

=

cos

cos

=

1

−sin

cos

=

2

2

2

2

2

∫

x

dx −2

∫

2

x

d

x

x

2

3

x

+C.

=

cos

sin

sin

= 2 sin

−

sin

2

2

2

3

2

2

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

Вариант 1

1) ∫

dx

2)

∫x

1 − x2 dx

3) ∫

cos

3x

dx

(2x −

6

sin

3)

x

4) ∫xe2 xdx

5)

∫(x +1)ln xdx

6) ∫

dx

x

3

2

− x

7) ∫

(2x −1)dx

8)

(2x +3)dx

9) ∫

x −1

∫

x +1 dx

x2 −5x +6

x2 +3x −5

10) ∫cos3 xdx

11) ∫cos 2x cos 3xdx

Вариант 2

1) ∫sin 3 x cos xdx

2) ∫

ln x dx

3) ∫

2x −3dx

x

dx

4) ∫x cos 2xdx

5) ∫3x ln 2xdx

6) ∫

x

4

−1

(x +1)dx

(2x −6)dx

7) ∫

8) ∫

9) ∫

1 − x

2

dx

x

2

− x −6

x

2

−6x + 2

10) ∫cos2 3xdx

11) ∫sin 2x cos xdx

6

1)∫cos 2x − π dx

6

4) ∫x sin 3xdx

7) ∫x2 +2xx −6 dx

10) ∫tg2 xdx

1)∫sin 3x + π dx

3

4) ∫				xdx
		cos			2	x
7) ∫				x −2				dx
	x		2	−4x +3

10) ∫sin 2 x cos2 xdx

1) ∫23xdx+1

4) ∫xe3x dx

7) ∫			x + 2		dx
	x	2	−2x +1

10) ∫sin 3 xdx

	Вариант 3
2) ∫3	x34dx	3) ∫xe−x2 dx
	x +4		x −1
5) ∫x arctg xdx		6) ∫
				dx
			x3 +1
8) ∫	(22x +6)dx	9) ∫	dx3		x	2
	x +6x −5		x +

11) ∫sin x sin 2xdx

Вариант 4

2) ∫		xdx			3) ∫	(arctg x)2
										dx
	x	2	+4			1	+ x	2
5) ∫x ln 3xdx							2x +1
						6) ∫ x3 −1 dx
		(x −1)dx							dx
8) ∫		x2 −2x +6				9) ∫3 x +1

11) ∫cos 2x cos xdx

Вариант 5

2) ∫	cos x			3) ∫			dx
			dx
	sin 2 x					x ln x
5) ∫arccos xdx				6) ∫		(2x −1)dx
						x	4	+5x		2	+4
8) ∫ (2x2		−1)dx
				9) ∫ 4 − x2 dx
	x	− x +5

21

11)∫cos 3 x cos 3 xdx

7

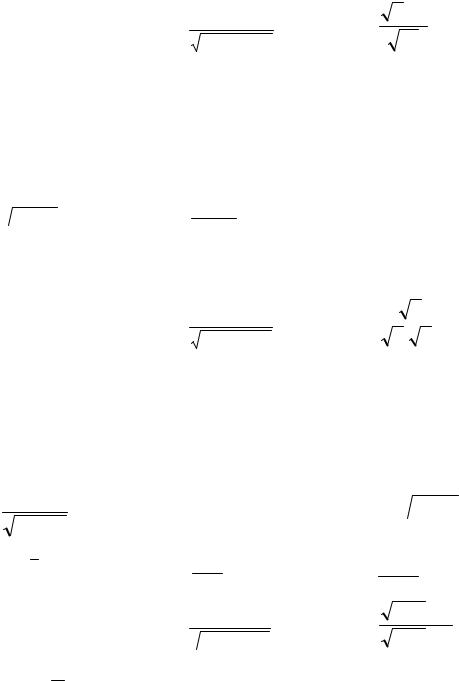
1) ∫(3x +5)5 dx

4) ∫x cos 4xdx

7)	∫	xdx
		(x −1)(x2 −4)

10) ∫sin 2 3xdx

1) ∫ 8 −2xdx

4) ∫(x +1)2 ln xdx

7) ∫			2x −3	dx
	x	2	+5x −6

10) ∫cos4 xdx

1) ∫ 1+dx4x2

−x

4)∫xe 3 dx

7) ∫	xdx
	(x −1)(x + 2)	2

10) ∫sin 2 2x dx

Вариант 6

2) ∫tg 2xdx

5) ∫ln 3xdx

8) ∫	(x2	+1)dx
	x	+ 2x +3

11) ∫cos 6x cos 2xdx

Вариант 7

x2

2) ∫x3 +9dx

5) ∫x sin		x	dx
	2
8) ∫	(22x −5)dx
	x −5x +3

11) ∫sin 7x cos xdx

Вариант 8

2) ∫ctg 3xdx

5) ∫lnx2x dx

8) ∫ (4x +6)dx

x2 +3x −1

11) ∫sin 3x cos xdx

8

3) ∫ex sin ex dx

6) ∫	x3	−2x +5			dx
		x	4	−1

9) ∫3 6 xx+5 1 dx

3) ∫		tg x			dx
		cos	2	x
6) ∫		(x +1)dx
	(x −2)(x2 +9)
9) ∫			x +1					dx
			4			4)
		x (		x +

3) ∫ex 1 + ex dx

6) ∫2x +5 dx x3 −1

9) ∫	x +1	+2 dx
	x +1	−2

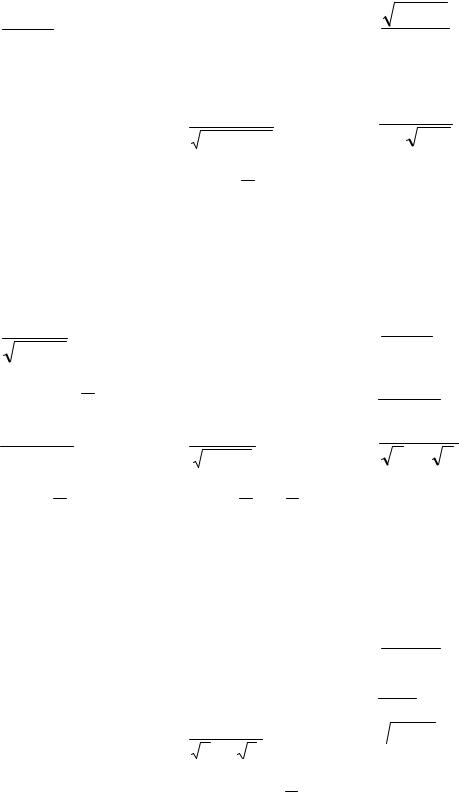
1) ∫1+dx9x2

4) ∫(x +1)cos 3xdx

7) ∫				x −3			dx
	x	2		−5x + 4
10)	∫		1		−tg x	dx
			1		+tg x

1) ∫	dx2	+1
	4x

4) ∫(x +1)sin 2x dx

7) ∫x2 −3xdx4x + 4

10) ∫cos2 3x dx

1) ∫3−x dx

4) ∫(x + 2)ex dx

7) ∫		3x −2				dx
	4x	2	−4x	+1

10) ∫cos3 2xdx

Вариант 9

sin xdx 2) ∫ cos3 x

5) ∫x arctg xdx

8) ∫	(22x −5)dx
	x −5x +6

11) ∫cos3 2x dx

Вариант 10

2) ∫cos x esin x dx

5) ∫x2 ln xdx

8) ∫(2x +5)dx

3 x2 +5x

11) ∫sin 2 x cos x dx
2	2

				Вариант 11
2) ∫		2x2 dx
		5	+3x	3
5) ∫ex sin 2xdx
8) ∫			dx
			x (3 +3 x )

x

11) ∫cos 3x cos 2 dx

9

3) ∫	arctg x				dx
	1	+ x	2
6) ∫		x2 + x					dx
	(x −1)(x +			2)		2

9) ∫4 +33dxx +1

tg3 x

3) ∫cos2 x dx

6)∫x3 − x −3 dx

x4 −4x2

9) ∫ x (1dx+3 x )

ctg 2x

3) ∫sin 2 2x dx

6)∫x3 +1 dx

x4 −1

9) ∫ 9 − x2 dx

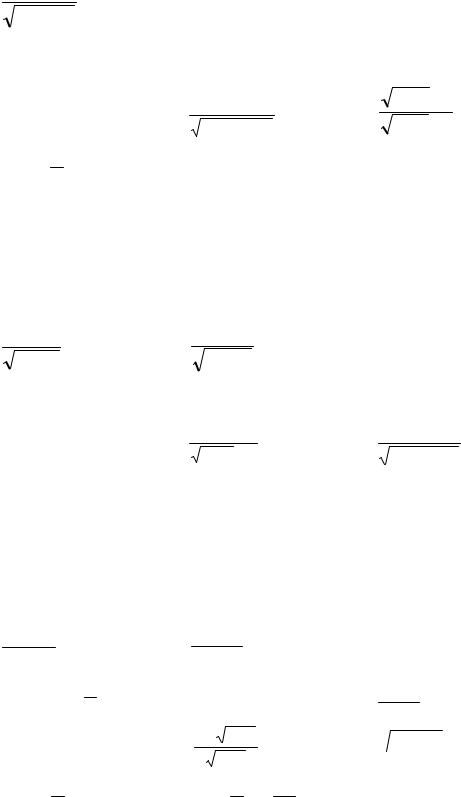
1) ∫				dx		2
			1−25x
4) ∫		ln		x	dx
				3
			x
7) ∫				3x −1			dx
	x		2	+8x +12

10) ∫sin 2 2x dx

1) ∫	dx
	4 −3x

4) ∫(2x −1)cos xdx

7) ∫			5x + 4	dx
	x	2	−8x +12

10) ∫tg3 xdx

dx

1) ∫4x2 +3

4) ∫(x −1)cos 2x dx

7) ∫			3xdx
	x	2	− x −12

10) ∫sin 2 3x dx

Вариант 12

2) ∫xex2 dx

5) ∫(x +3)sin 2xdx

8)	∫	(x +1)dx
		4	− x	2	−2x

11) ∫sin x sin 2xdx

Вариант 13

2)∫ 1e−xe2 x dx

5)∫ln 3xdx

8) ∫	dx
	x + 2 −4
11) ∫sin		5 x cos	3 xdx
		2	2

Вариант 14

edx

2)∫e2 x +9

5)∫x2 ln xdxx

8) ∫1 +3x x++1 1 dx

∫x 3x

11)sin 2 sin 2 dx

10

3) ∫sin ln x dx
			x
6) ∫		x + 2		dx
	x	3	+ 4x
9) ∫			x +2 −1 dx
			x +2 +1

	5
3) ∫		tg x		dx
		2
		cos	x
6) ∫		4xdx
	(x +1)(x2 + 2)
9) ∫		(x −32 )dx
		1 − x	+6x

3) ∫3xe−2 x2 dx

6)∫ 2x −1 dx

x3 + x

9) ∫ 16 − x2 dx