2.4Метрические характеристики графов

Длиной маршрута называется количество ребер в нем (с повторениями). Если маршрут М = v₀, e₁, v₁, e₂, v₂ ,..., e_k, v_k, то длина М равна k (обозначается |М| = k).

Расстоянием между вершинами u и v (обозначается d(u, v)) называется длина кратчайшей цепи , а сама кратчайшая цепь называется геодезической.

Однако если не существует цепи , то полагают d(u, v) = +.

Свойства расстояния d(u, v):

4. d(u, u) = 0;

5. d(u, v) 0;

6. В неориентированном графе d(u, v) = d(v, u);

7. d(u, v) + d(v, w)  d(u, w).

Рассмотрим неориентированный граф G. Для фиксированной вершины v величина называется эксцентриситетом или отклоненностью вершины v. Минимальный из эксцентриситетов вершин графа G называется радиусом графа . Максимальный из всех эксцентриситетов вершин графа G называется диаметром графа .

Диаметр графа равен длине длиннейшей геоде­зической, т.е. длине длиннейшей кратчайшей цепи графа.

Множество вершин, находящихся на одинаковом расстоянии n от вершины v (обозначение D(v,n)), называется ярусом:

.

2.5Связность графов

Говорят, что две вершины в графе связаны, если существует соединяющая их (простая) цепь. Граф, в котором все вершины связаны, называется связным.

Отношение связанности вершин является эквивалентностью. Классы эквива­лентности по отношению связанности называются компонентами связности гра­фа. Число компонент связности графа G обозначается k(G). Граф G является связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G — несвязный граф. Граф, состоящий только из изолированных вершин (в котором k(G) = p(G) и r(G) = 0), называется вполне несвязным или пустым.

3Виды графов

3.1Тривиальные и полные графы

Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с k вершинами, обозначается C_k, например С₃ – треугольник.

Граф, в котором каждая пара вершин смежна, называется полным. Полный граф с р вершинами обозначается К_р, он имеет максимально возможное число ребер

.

Полный подграф некоторого графа называется кликой этого графа.

3.2Двудольные графы

Двудольный граф (или биграф, или четный граф) — это граф G(V, E), такой что множество V разбито на два непересекающихся множества V₁ и V₂ ( ), причем всякое ребро из Е инцидентно вершине из V₁ и вершине из V₂ (то есть соединяет вершину из V₁ с вершиной из V₂). Множества V₁ и V₂ называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющие множества V₁ и V₂, то он называется полным двудольным графом. Если |V₁| = m и |V₂| = n, то полный двудольный граф обозначается K_m,n. В качестве примера на рис. 8 приведена диаграмма графа К_3,3.

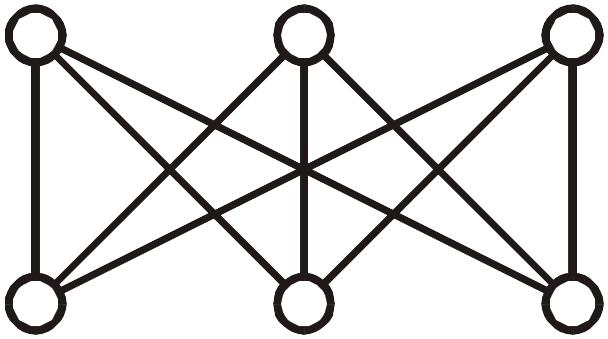
Рис. 8. Диаграмма двудольного графа K_3,3

Относительно двудольных графов имеет место следующая теорема: Граф является двудольным тогда и только тогда, когда все его про­стые циклы имеют четную длину.

3.3Планарные и плоские графы

Граф называется планарным, если его можно изобразить на плоскости таким образом, чтобы его ребра не пересекались в точках, отличных от вершин. Граф, множество ребер которого расположено на плоскости таким образом, что ребра не пересекаются в точках, отличных от вершин, называется плоским.

Таким образом, планарный граф – это граф, который можно уложить на плоскости, а плоский граф – это граф, уже уложенный на плоскости. На рис. 9 представлены диаграммы планарного и изоморфного ему плоского графов.

Рис. 9. Планарный и изоморфный ему плоский графы

Область плоскости, ограниченная ребрами плоского графа, внутри которой нет ни вершин, ни ребер, называется гранью и обозначается f_i. Ребра грани образуют простой цикл. Считается, что всякий плоский граф имеет одну бесконечную грань, т.е. часть внешней плоскости, окружающей граф.

Имеет место формула Эйлера , где f – количество граней плоского графа.

Количество граней плоского графа не зависит от способа укладки его на плоскость и равно .

Планарный граф, который при добавлении любого ребра становится не планарным, называется максимально планарным графом. Минимальное число ребер, которое необходимо удалить из графа, чтобы он стал планарным, называется числом планарности графа. Граф, не имеющий ни одного цикла всегда планарен.