2.3. Частные случаи движения точки

Равномерным называется такое движение, при котором проекция скорости на касательную к траектории постоянна, т.е. V, = const и, следо вательно, а_т=0.

Поэтому, а = а_п = V ² / p, т.е. при равномерном криволинейном движении точки полное ускорение равно нормальному. Скорость же при таком движении, оставаясь постоянной по величине, изменяет лишь свое направление. Отсюда следует, что нормальное ускорение характеризует быстроту изменения скорости по направлению.

Движение точки называется переменным, если величина ее скорости изменяется с течением времени. Если при этом величина скорости увели­чивается, то движение называется ускоренным, если уменьшается - замед­ленным. Поскольку точка совершает прямолинейное движение, то в любой точке ее траектории р = оо и, следовательно, а_п = 0.

Таким образом, а = а_п= V ² / p т.е. полное ускорение равно тангенциальному. Скорость же при таком движении изменяет лишь свою величину. Отсюда следует, что тангенциальное ускорение характеризует быстроту изменения величины скорости.

При равномерном прямолинейном движении скорость точки не изме­няется ни по величине, ни по направлению.

Равнопеременным движение точки называется такое движение, при котором ее тангенциальное ускорение постоянно, т.е. а_т = const.

2.4. Динамика поступательного и вращательного движения

Простейшими видами движения твердого тела являются по­ступательное движение и вращение вокруг неподвижной оси. Под твердым телом в кинематике, как и в статике, понимается абсолютно твердое тело.

Рассмотрим основные свойства и зависимости между кинематически­ми параметрами поступательного и вращательного движений твердого те­ла. Заметим, что поступательное или вращательное движение может со­вершать только твердое тело.

Установим взаимосвязь между кинематическими параметрами вра­щательного движения твердого тела вокруг неподвижной оси и движения точки, принадлежащей этому телу. Важное значение здесь имеет передача вращательного движения от одного вала машины к другому. В этом разделе мы выведем зависимость между угловыми скоростями двух валов при передаче вращательного движения от одного к другому. Здесь же мы ознакомимся с двумя новыми векторами - с вектором угловой скорости и вектором углового ускорения твердого тела, вращающегося вокруг неподвижной оси. С помощью этих векторов мы выведем векторные формулы скорости и ускорения точки, принадле­жащей вращающемуся твердому телу, которые будем впоследствии ис­пользовать как в кинематике, так и в динамике.

2.4.1. Поступательное движение твердого тела

а) Определение и классификация поступательного движения

Поступательным движением твердого те­ла называется такое его движение, при котором любая прямая, неизменно связанная с телом, за все время его движения остается параллельной своему начальному положению. Поступательное движение совершает, например, вагон, движу­щийся по прямолинейному участку пути.

В ка­честве второго примера поступательного движе­ния можно привести движение спарника АВ (рис. 2.5), соединенного шарнирно с концами двух равных по длине кривошипов О₁А и О₂В, вращающихся в одинаковых направлениях вокруг перпендику­лярных к ним параллельных между собой осей О₁ и О₂, отстоящих друг от друга на расстоянии, равном длине спарника. Описанный механизм назы­вается шарнирным параллелограммом. При любом положении этого меха­низма сохраняется параллельность между прямой, проходящей через цен­тры шарниров A и В и неподвижной прямой O_t O₂. Таким образом, любая прямая CD, неизменно связанная со спарником и, следовательно, обра­зующая с прямой АВ постоянный угол а, образует такой же постоянный по величине угол и с параллельной ей неподвижной прямой О₁,О₂. Отсюда следует, что за все время движения спарника упомянутая прямая остается параллельной своему начальному положению, т. е. спарник движется по­ступательно. Если при поступательном движении твердого тела все его точки движутся прямолинейно, то такое поступательное движение называется прямолинейным. В противном случае поступательное движение называется криволинейным.

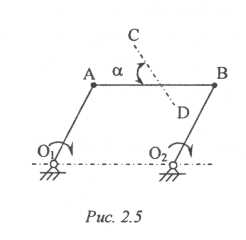
Например, прямолинейное поступательное движение совершает ва­гон, движущийся по прямолинейному участку пути или поршень, движу­щийся в цилиндре двигателя. Спарник АВ, показанный на рис. 2.5, совер­шает криволинейное поступательное движение, так как точки его описы­вают траектории, например, точки А u В движутся по окружностям одина­кового радиуса с центрами в точках О₁ и О ₂.

Если при поступательном движении твердого тела все его точки пе­ремещаются в плоскостях, параллельных некоторой неподвижной плоско­сти, то такое движение тела называется плоским поступательным. Плос­кое поступательное движение совершает, например, спарник, показанный на рис. 2..5, так как все его точки перемещаются в плоскостях, параллель­ных неподвижной плоскости, проведенной перпендикулярно к осям О₁ и О₂ вращения кривошипов. Траектории всех точек твердого тела, совер­шающего плоское поступательное движение, расположены в параллельных плоскостях и, следовательно, представляют собой плоские линии. Понят­но, что прямолинейное поступательное движение твердого тела является частным случаем плоского поступательного движения.

Если все точки поступательно движущегося твердого тела описыва­ют пространственные кривые, то такое движение тела называется про­странственным поступательным.

б) Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении

Прежде чем сформулировать эту теорему, напомним о следующих определениях, известных из элементарного курса геометрии.

Определение 1. Две фигуры называются конгруэнтными, если при наложении одной из них на другую они совмещаются всеми своими точ­ками.

Определение 2. Точки двух конгруэнтных фигур, совмещающиеся друг с другом при их наложении, называются соответствующими точками.

Определение 3. Две конгруэнтные фигуры называются смещенными относительно друг друга параллельно, если их соответствующие точки смещены относительно друг друга по параллельным прямым на одинако­вые расстояния.

Теперь сформулируем следующую теорему.

Теорема 1. Все точки поступательно движущегося твердого тела описывают конгруэнтные параллельно смещенные траектории и имеют в любой момент равные векторы скорости и равные векторы ускорения.

Пусть некоторое твердое тело (рис. 2.6) совершает поступательное движение относительно системы отсчета O x y z. Возьмем две произвольные

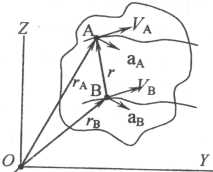
его точки А и В и докажем, что они дви­жутся по конгруэнтным параллельно сме­щенным траекториям, имея в любой мо­мент времени равные векторы скорости Vа и Vв и равные векторы ускорения а_А и а_В , т.е.

V _A =V_B и а_А =а _В

Для доказательства проведем в точки А и В радиусы-векторы r_А и r_в из на­чала координат О. Проведем также вектор ВА = r. Этот вектор постоянен по величине, так как рассматриваемое тело является абсолютно твердым и, следовательно, расстояние между точками А и В при его движении остает­ся неизменным.

Направление этого вектора также не изменяется, так как, согласно условию, тело движется поступательно, и, поэтому, прямая, про­ходящая через точки А и В, перемещается параллельно своему начальному положению.

Таким образом, вектор r постоянен, т. е. r = const. (2.7)

Следовательно, траекторию точки В можно совместить всеми ее точ­ками с соответствующими точками траектории точки А путем параллель­ного переноса их в направлении вектора r на одинаковые расстояния, рав­ные длине отрезка АВ, чем и доказана первая часть сформулированной теоремы. Из векторного треугольника ОBА замечаем, что г_А = г_в + г . (2.8)

в) Уравнения поступательного движения твердого тела Теперь мы знаем, что все точки поступательно движущегося твердо­го тела совершают одинаковые движения: по конгруэнтным параллельно смещенным траекториям, с одинаковыми по величине и направлению ско­ростями и ускорениями. Одинаковые для всех точек тела траектории, ско­рости и ускорения называются соответственно траекторией, скоростью и ускорением твердого тела. Отсюда следует, что для исследования поступа­тельного движения твердого тела достаточно исследовать движение какой-либо одной его точки, так как все остальные его точки совершают такие же движения. Эта точка называется полюсом. За полюс может быть принята любая точка данного тела. Например, все точки спарника АВ, показанного на рис. 2.5, движутся по окружности одинакового радиуса, равного длине кривошипов О,А и О₂В, а их скорости и ускорения равны по величине ско­ростям и ускорениям точек А и В и одинаковы с ними по направлению. Та­ким образом, в этом примере за полюс можно принять точку А или В.

Движение полюса может быть определено любым из способов, описанных в предыдущей теме: векторным, координатным или естественным.

Например, если принять за полюс точку В (рис. 2.6), то движение его мож­но определить следующим векторным уравнением:

r_B=f_B(t) (2.11)

Из векторной зависимости (2.8) замечаем, что векторное уравнение движения любой другой точки данного тела отличается от (2.11) на посто­янный вектор. Например, для точки А имеем:

r _а=f_в(t) (2.12)

Таким образом, уравнение (2.11) определяет движение любой точки данного тела. В связи с этим это уравнение называется уравнением посту­пательного движения твердого тела в векторной форме.

Движение полюса В можно определить и уравнениями движения в координатной форме:

x_B=f ₁(t),

y_b=f₂(t) (2-13)

z_B=f ₃(t)

Уравнения движения любой другой точки данного тела отличаются от уравнений (2.13) постоянными членами. Например, для точки А будем иметь:

x_B=f ₁(t) +r _x

y_b=f₂(t)+r_x (2-14)

z_B=f ₃(t)+r_z

где r_x r_y r_z проекции на координатные оси постоянной вектора г . Таким образом, уравнения (2.13) определяют движение любой точки дан­ного тела и называются уравнениями поступательного движения твердого тела в координатной форме.

Аналогично, движение полюса В можно определить естественным способом с помощью уравнения: S_B=f_B(t). (2.15)

Это уравнение называется уравнением поступательного движения твердо­го тела в естественной форме. Уравнение движения других точек данного тела отличаются от него лишь постоянными членами, которые не оказы­вают влияние на скорость и ускорение его точек.

2.4.2. Уравнение вращения твердого тела вокруг неподвижной оси

Если две точки А и В (рис. 2.7а) твердого тела закреплены неподвижно, то это тело сможет совершать только такое движение, при котором будут оставаться неподвижными все его точки, лежащие на прямой, проходящей через эти точки.

Эта прямая называется осью вращения. Оси вращения Z, как и всякой другой оси, приписывается определенное направление, считаемое положи­тельным.

Представим себе две полуплоскости Р и Q (рис. 2.7), ограниченные с одной стороны осью вращения Z, первая из которых неизменно связана с некоторой системой отсчета и, следовательно, условно считается непод­вижной, а вторая — с вращающимся твердым телом и, поэтому, вместе с ним вращается вокруг оси Z. На рис. 2.7 ось Z перпендикулярна к плоскости чертежа и, следовательно, на нем показаны лишь следы полуплоскостей Р и Q на этой плоскости.

Положение твердого тела однозначно оп­ределяется двугранным углом φ, образованным упомянутыми полуплоскостями, если считать его величиной алгебраической. Этот угол назы­вается угловой координатной твердого тела. Его принято считать положительным, если, при взгляде с положительного направления оси вращения, подвижная полуплоскость повернута относительно неподвижной против хода стрел­ки часов, и отрицательным в противном случае. Не следует смешивать угловую коорди­нату твердого тела с углом его поворота.

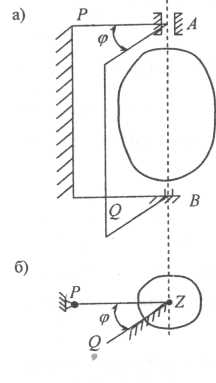
По­следний, как и путь, пройденный точкой, всегда положителен и может только увеличиваться, независимо от направления вращения тела.

Угловая координата, как правило, измеряется в радианах, т.е. являет­ся величиной безразмерной, и обозначается буквой φ. Иногда ее измеряют в полных оборотах тела и тогда обозначают буквой N. Поскольку один оборот содержит 2л радиан, то для перехода от одной единицы измерения угловой координаты к другой существует зависимость: φ = 2πN. (2.16)

При вращении твердого тела вокруг неподвижной оси его угловая координата, в общем случае, непрерывно изменяется с течением времени, т. е. является однозначной и, как показано ниже, дважды дифференцируе­мой функцией времени t, т.е.

φ = f(t). (2.17)

Уравнение такого вида определяет вращательное движение твердого тела и называется уравнением его вращения вокруг неподвижной оси.

2.4.3. Угловая скорость и угловое ускорение твердого тела

Угловая скорость твердого тела, вращающегося вокруг неподвижной оси, характеризует быстроту его вращения вокруг этой оси. Пусть в мо­мент t угловая координата тела равна φ, а в момент t_x = t + Δt она равна φ = φ + Δφ. Следовательно, в течение бесконечно малого промежутка времени At тело поворачивается на бесконечно малый угол Δφ. Величина ω_ср = Δφ / Δt называется средней угловой скоростью тела за промежуток вре­мени Δt. Предел средней угловой скорости при Δt —0 называется угловой скоростью твердого тела в момент t и обозначается ω, т.е. ω =dφ / dt,

Таким образом, угловая скорость твердого тела, вращающегося во­круг неподвижной оси, равна первой производной его угловой координаты по времени.

Поскольку производная - dφ / dt, положительна при возрастании угловой

координаты φ и отрицательна в противном случае, то угловая скорость ω является величиной алгебраической. Она положительна, если тело враща­ется в сторону положительных угловых координат, т.е. против хода стрел­ки часов при взгляде с положительного направления оси вращения, и от­рицательна, если тело вращается в противоположном направлении.

Если угловую координату измерять в радианах, а время - в секундах, то, учтя, что радиан есть величина безразмерная, получим для угловой скорости ω размерность с' .

Иногда угловую скорость равномерного вращения твердого тела из­меряют числом его оборотов в минуту. В этом случае ее обозначают п. Между угловой скоростью ω (с ) и числом п (об/мин) существует зависи­мость: ω = πn / 30

Число п оборотов тела в минуту часто называют частотой его вращения.

Быстрота изменения угловой скорости характеризуется величиной его углового ускорения.

Пусть в момент t угловая скорость тела равна ω, а в момент t =t + Δt она равна

ω = ω + Δω. Тогда в течение бесконечно малого промежутка времени Δt угловая скорость тела изменяется на бесконечно малую величину Δω. Величина ε_ср = Δω / Δt называется средним угловым ус­корением тела за промежуток времени Δt,, а ее предел при Δt —0 — угловым ускорением в момент t и обозначается ε, ε= dω / d t = d ²φ / d ²t =φ

Эта зависимость подтверждает высказанное выше предположение о том, что функция (2.17) должна быть дважды дифференцируемой.

Таким образом, угловое ускорение твердого тела, вращающегося во­круг неподвижной оси, в момент t равно первой производной его угловой скорости по времени или второй производной по времени его угловой ко­ординаты.

Угловое ускорение, также как и угловая скорость, является величи­ной алгебраической. Оно положительно, если угловая скорость увеличива­ется с течением времени и отрицательно в противном случае. Иными сло­вами, тело совершает ускоренное вращение, если угловая скорость и угло­вое ускорение имеют одинаковые знаки, и замедленное - если их знаки различны. Измеряется угловое ускорение в с^-2.

2.4.5. Плоское движение твердого тела

После ознакомления с кинематикой поступательного и вращательно­го движений твердого тела можно перейти к изучению кинематики более сложного его движения. Таким движением является плоское движение твердого тела.

П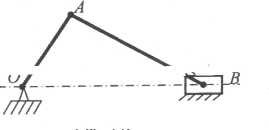 лоским движением твердого тела называется такое его движение, при котором все его точки перемещаются в плоскостях, параллельных не­которой неподвижной плоскости, называемой основной плоскостью. Плоское движение совершает, например, колесо, катящееся по прямоли­нейному рельсу, или шатун АВ (рис. 2.8) кривошипно-ползунного механизма, со­стоящего из кривошипа ОА, вращающегося

вокруг неподвижной оси О, перпендикулярной к плоскости чертежа, соединенного ним шарнирно шатуна АВ и ползуна В,

помещенного в горизонтальные направляющие и соединенного шарнирно с шатуном. Вращение твердого тела вокруг неподвижной оси и плоское поступательное движение являются частными случаями плоского движе­ния.

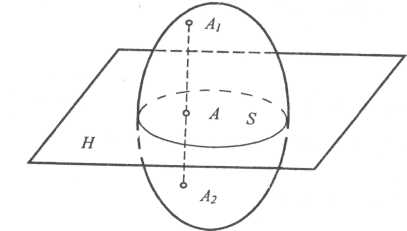
Пусть некоторое твердое тело (рис. 2.9) совершает плоское движе­ние. Понятно, что в этом случае плоская фигура S, образованная в сечении тела основной плоскостью Н (или плоскостью, ей параллельной), за все время движения тела остается в этой плоскости. Прямая A_tA₂, проходящая через произвольную точку А и фигуры S, перпендикуляр­ная к плоскости Н и неизмен­но связанная с рассматривае­мым телом, за все время дви­жения тела остается перпен­дикулярной к этой плоскости, т.е. совершает поступатель­ное движение Рис. 2.9. Следовательно, все точки этой прямой соверша­ют одинаковые движения.

То же самое можно сказать про точки прямых, параллельных прямой А,А₂, проходящих через все остальные точки фигу­ры S. Отсюда следует, что все сечения данного тела плоскостями, парал­лельными плоскости Н, совершают одинаковые движения, следовательно, движение фигуры S в ее плоскости определяет плоское движение рассмат­риваемого твердого тела. Поэтому в дальнейшем вместо плоского движе­ния твердого тела мы будем исследовать движение плоской фигуры в ее плоскости.