
- •Государственное образовательное учреждение высшего профессионального образования
- •Исследование одной краевой задачи на графе для струнной системы с циклом
- •010109 – Функциональный анализ
- •Оглавление
- •1. Основные понятия теории краевых задач на графах
- •2. Постановка краевой задачи.
- •3. Невырожденность.
- •Построение функции Грина задачи.
- •Решение дифференциального неравенства .
3. Невырожденность.
Рассмотрим неоднородную задачу (2.1) – (2.7).
По левым частям
равенств (2.1) – (2.6) построим функционалы
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
По левой части равенства (2.7) построим дифференциальный оператор:

Тогда неоднородная задача (2.1) – (2.7) сводится к задаче:
![]() ,
,
![]() .
(3.1)
.
(3.1)
А однородная задача (2.1) – (2.7’) к задаче:
![]() ,
.
(3.2)
,
.
(3.2)
Теорема 2. (Условие невырождености).
Задача (3.1) для имеет только тривиальное реше- ние.
Доказательство.
Так как
![]() на
,
,
то
на
,
,
то
![]() ,
,
В частности на
имеем
![]()
Возможны 3
случая:
![]() ,
,
![]() ,
,
![]() .
.
Если
Из
![]() следует, что функция
следует, что функция
![]() возрастает от
точки
возрастает от
точки
![]() до
до
![]() ,
и так как
,
то
,
и так как
,
то
![]() на
.
Тогда
на
.
Тогда
![]() .
.
Из условия
непрерывности (2.3) имеем:
![]() .
.
Из условия (2.5) получим,
![]() =
=![]() ,
что равносильно равенству:
,
что равносильно равенству:
![]()
Из
![]() следует, что функция
следует, что функция
![]() возрастает от
точки
до
возрастает от
точки
до
![]() ,
и так как
,
то
,
и так как
,
то
![]() на
.
Тогда,
на
.
Тогда,
![]() ,
что из условия непрерывности (4) имеем:
,
что из условия непрерывности (4) имеем:
![]() .
.
Из условия (2.6) получим:
![]() =
=![]() ,
что равносильно равенству:
,
что равносильно равенству:
![]() .
.
Из
![]() следует, что функция
следует, что функция
![]() возрастает от
точки
до
,
и так как
,
то
возрастает от
точки
до
,
и так как
,
то
![]() на
.
Тогда,
на
.
Тогда,
![]() ,
что противоречит (2.2). Следовательно
случай
невозможен.
,
что противоречит (2.2). Следовательно
случай
невозможен.
Аналогично, при так же придем к противоречию (2.2)
Если .
Из
![]() следует, что функция
следует, что функция
![]() ,
и так как
,
то
,
и так как
,
то
![]() на
.
Следовательно,
на
.
Следовательно,
![]() .
.
Из условия непрерывности (2.3) и условия (2.5), имеем:
=![]() .
.
Тогда
![]() ,
и
,
и
![]() ,а
это означает, что
,а
это означает, что
![]() на
.
Следовательно,
на
.
Следовательно,
![]() ,
что по условию непрерывности (2.4) означает:
,
что по условию непрерывности (2.4) означает:
![]() .
.
Из равенства (2.6) имеем,
=![]() .
.
Тогда
![]() ,
и
,
и
![]() ,а
это означает, что
,а
это означает, что
![]() на
.
на
.
Итак, из трех рассмотренных случаев возможен только один:
,
при котором
![]() на
,
.
на
,
.
Итак,
![]() на Г.
на Г.
Построение функции Грина задачи.
Если задача (2.1) – (2.7) невырождена (т.е. имеет единственное решение) на Г, то ее решение для функции , и любой может быть представлено в виде:
![]() .
(4.1)
.
(4.1)
Определение.
Функцией Грина
![]() на отрезке называют функцию двух
переменных
на отрезке называют функцию двух
переменных
![]() и
и
![]() ,
при каждом фиксированном
из отрезка, обладающую свойствами:
,
при каждом фиксированном
из отрезка, обладающую свойствами:
1. при
![]() удовлетворяет по
однородному дифференциальному уравнению;
удовлетворяет по
однородному дифференциальному уравнению;
2. при удовлетворяет по краевым условиям;
3. при
![]() непрерывна по
,
т.е.
непрерывна по
,
т.е.
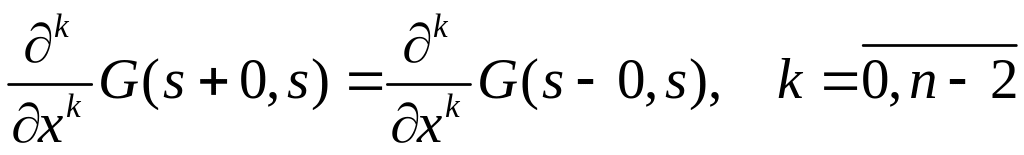 ,
,
(для уравнения
порядка
![]() )
)
4. при имеет скачек, т.е.
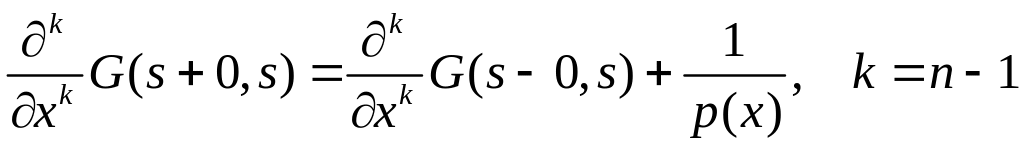 ,
,
(где
![]() - коэффициент при старшей производной
дифференциального уравнения порядка
).
- коэффициент при старшей производной
дифференциального уравнения порядка
).
Функцию Грина
задачи (2.1) - (2.7) на графе
![]() можно построить по формуле:
можно построить по формуле:
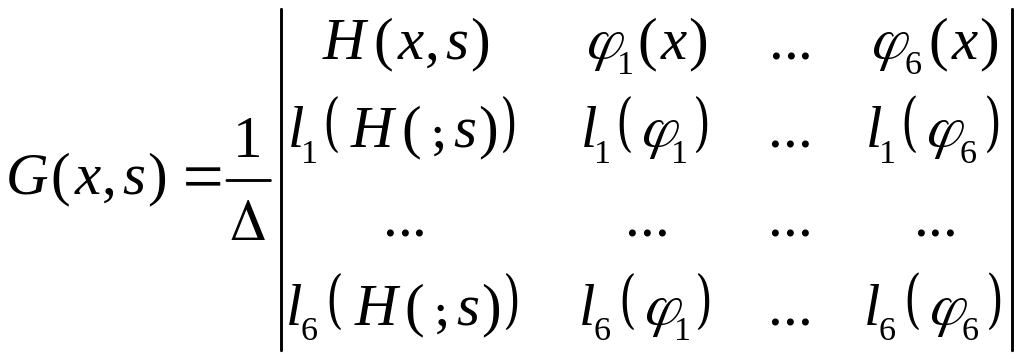 (4.2)
(4.2)
где
![]() - фундаментальная система решений
однородного уравнения
- фундаментальная система решений
однородного уравнения
![]() .
.
 (4.3)
(4.3)
Положим в задаче
(2.1) - (2.7)
![]() .
.
Функцию
![]() можно построить по функциям Грина
двухточечных задач (задач на отрезках)
на
:
можно построить по функциям Грина
двухточечных задач (задач на отрезках)
на
:
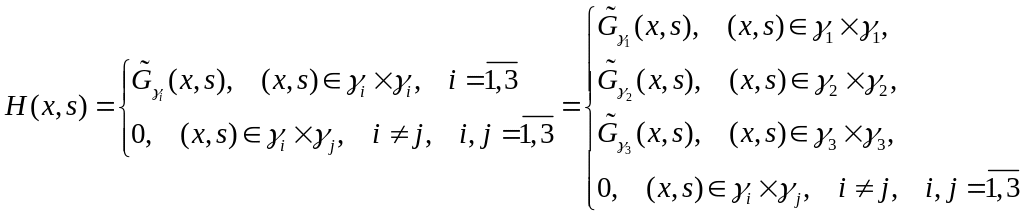 (4.4)
(4.4)
где
![]() -
функция Грина двухточечной краевой
задачи на отрезке
-
функция Грина двухточечной краевой
задачи на отрезке
![]() :
:
![]() на
,
на
,
![]() ,
(4.5)
,
(4.5)
![]() ,
,
(
)
,
,
(
)
Согласно определению
функции Грина на отрезке, она должна
удовлетворять однородному уравнению,
поэтому найдем фундаментальную систему
решений однородного уравнения
![]() :
:
![]() ,
,
![]() .
.
По левым частям
краевых условий (2.16) построим функционалы:
![]() ,
,
![]() .
.
Так как функция Грина должна удовлетворять краевым условиям, то
![]() ,
,
![]()
![]() ,
,
![]() .
(4.6)
.
(4.6)
Функцию Грина задачи (4.5) будем искать в виде:
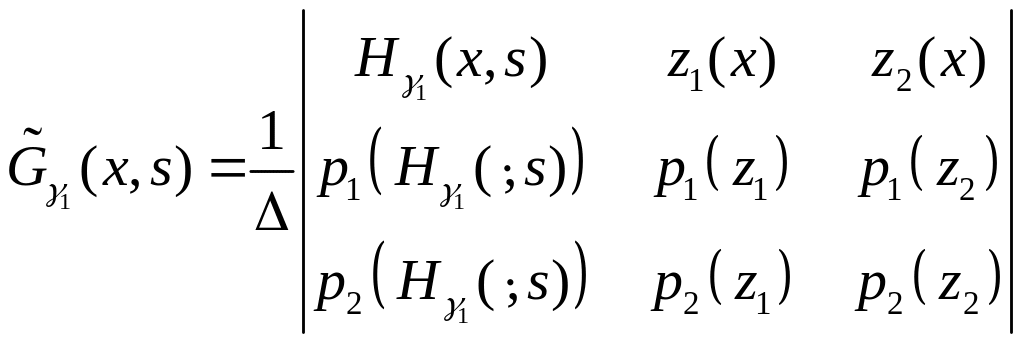 ,
,
где по равенствам
(4.6) можно найти
 ,
,
функция
![]() - какое-либо решение неоднородного
уравнения задачи (4.5), которое может быть
найдено, например, с помощью функции
Коши:
- какое-либо решение неоднородного
уравнения задачи (4.5), которое может быть
найдено, например, с помощью функции
Коши:
 .
.
Итак
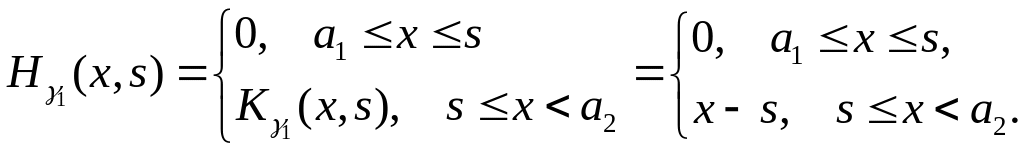
![]() ,
,
![]() .
.
Построим
![]() на
на
![]() :
:
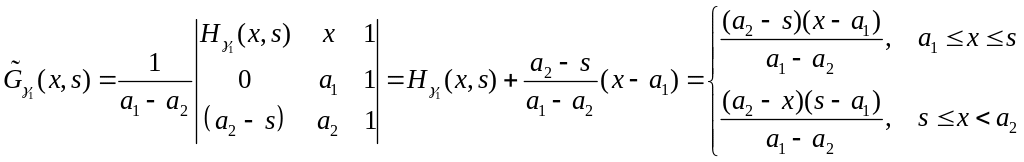
Аналогично
строим
![]() и
и
![]() :
:
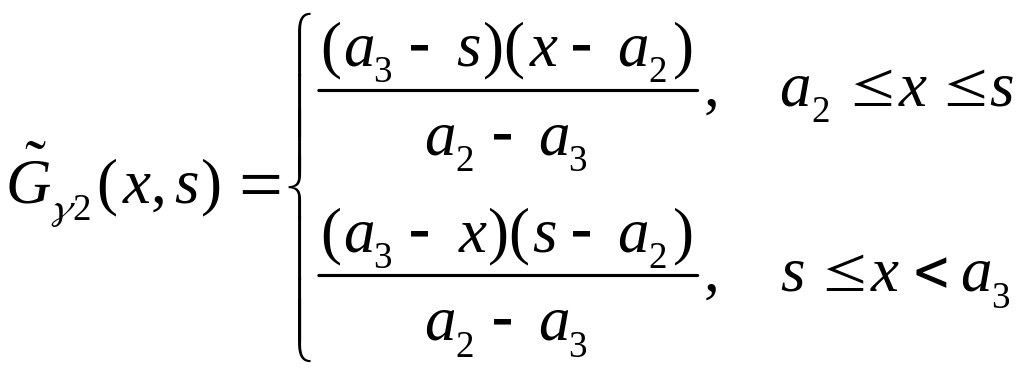 ,
,
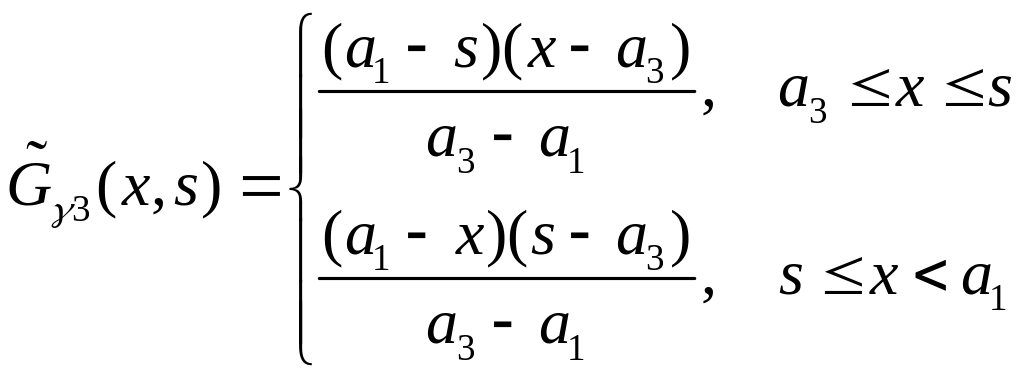
Построим
![]() по формуле (4.3):
по формуле (4.3):
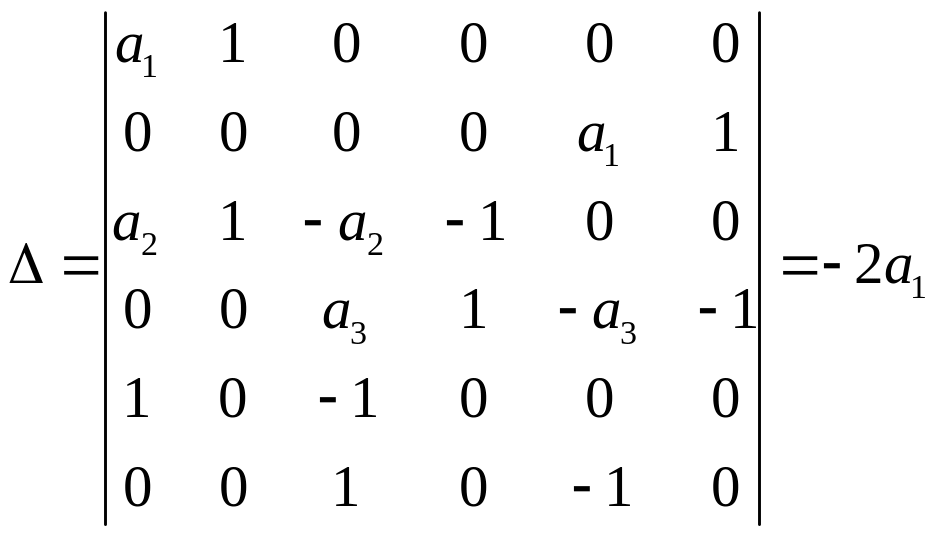 ,
,
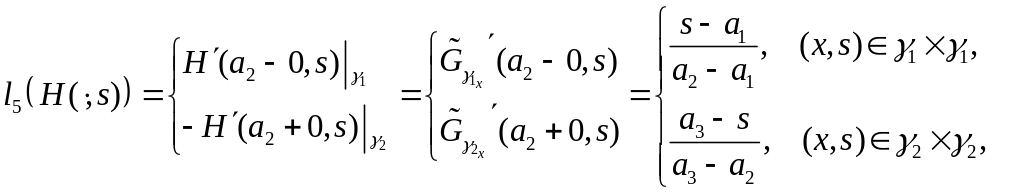
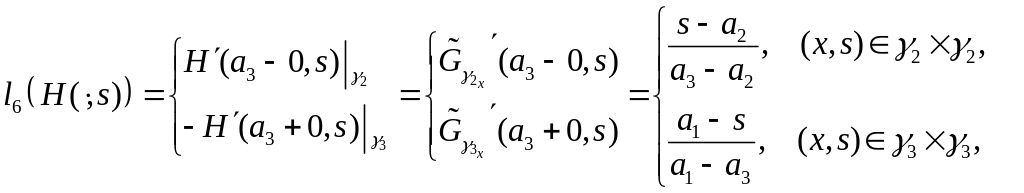
Тогда функция Грина задачи (2.1) - (2.7) определяемая по формуле (4.2), имеет вид:
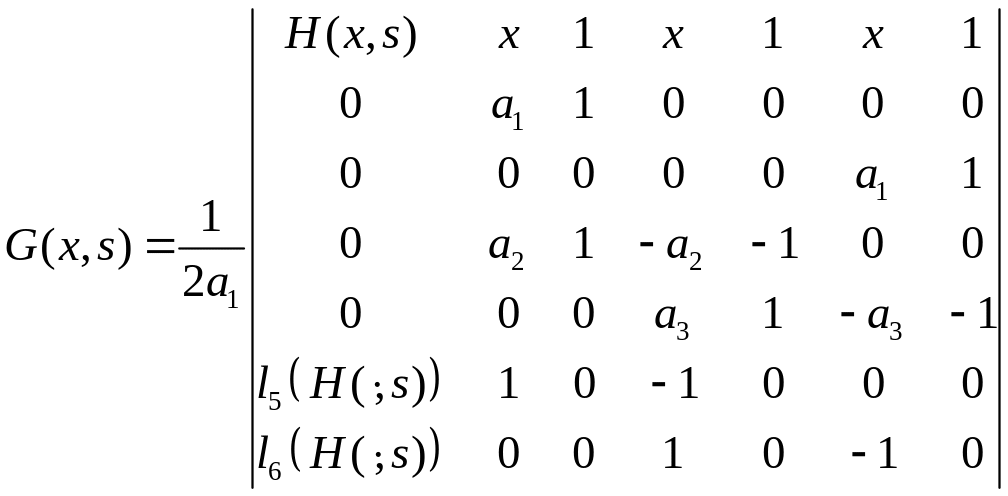 ,
,
где
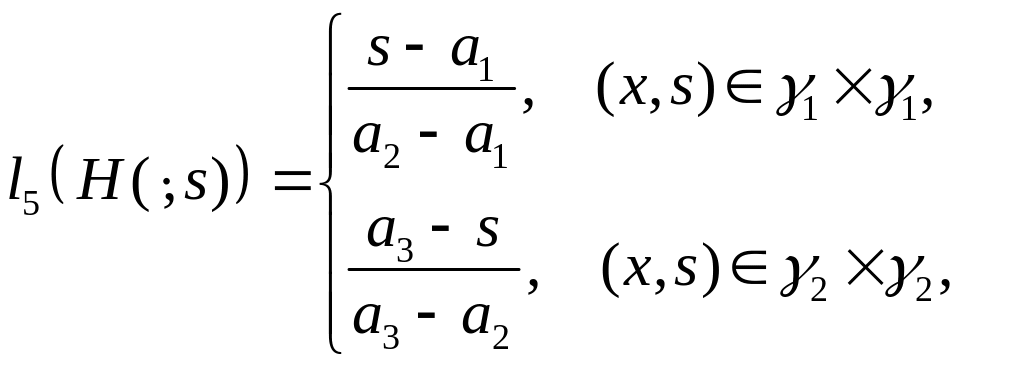 ,
,
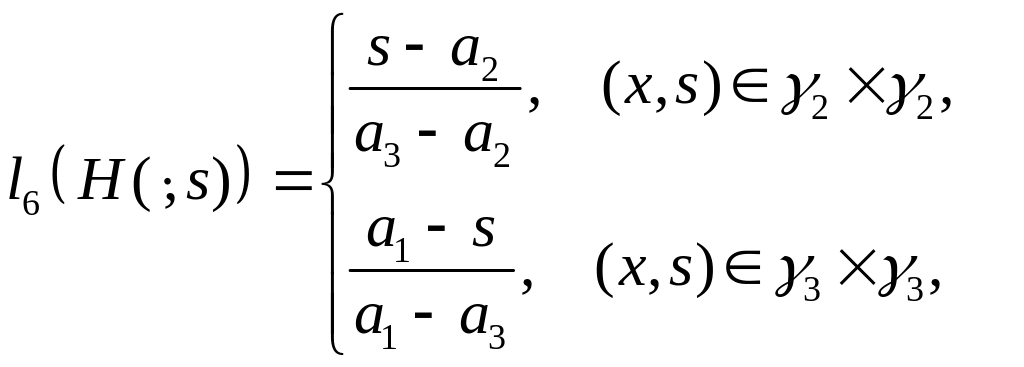
H(x,s) определяется по формуле (4.4).
