1.Вопросы по теме «общее представление об интеграле»

1.3 Определение меры

Мера множества

        математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (Δ) любого квадрата Δ полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов Δ₁, Δ₂,..., Δ_n,...; нижнюю грань чисел

         

      взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m^*(А)

множества А. Нижняя (внутренняя) мера m^* (А) множества А определяется как разность

         

        где Δ — какой-либо квадрат, содержащий множество А, и  А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значениеm (А) верхней и нижней мер — мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.         Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)Δ ́≥ ́0; 2) мера суммы

         

      конечной или счётной системы попарно непересекающихся множеств A₁, A₂..., A_n... равна сумме их мер:

         

  3) при перемещении множества как твёрдого тела его мера не меняется.

Мера Лебега первоначально была определена для множеств на действительной прямой и привела к теории интегрирования по таким множествам. Применительно к более общим множествам ее основные положения и результаты приводят к абстрактной теории интегрирования, в свою очередь имеющей многочисленные реализации и приложения. Исходным пунктом одной из таких абстрактных теорий стало аксиоматическое задание внешней меры, предложенное К.Каратеодори (1873-1950). Рассмотрим абстрактное пространство S. Предположим, что величина m*(A) определена для любого подмножества A из S. Эта функция множества m* называется "внешней мерой", если она удовлетворяет следующим условиям: 1) m*(f) = 0, если f - пустое множество; 2) m*(A) Ј m*(B), если A содержится в B; 3)

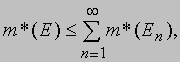если E1, E2, E3, ... - любая последовательность множеств, покрывающих множество E. Внешняя мера Лебега (описанная выше) обладает этими свойствами, причем оказывается, что для нее эти свойства являются определяющими. Если задана любая m*, удовлетворяющая этим условиям, то измеримость множеств определяется утверждением, что E измеримо, если для любого множества A выполняется соотношение m*(A) = m*(A З E) + m*(A - E). Здесь A З E (пересечение A и E) означает множество точек, принадлежащих одновременно A и E; а A - E - множество точек, принадлежащих A, но не принадлежащих E. Интуитивно измеримое множество воспринимается как "хорошее", и определение Каратеодори говорит о том, что множество E измеримо, если не существует такого множества А, которое бы разделяло Е на две части, внутреннюю и внешнюю, так, что их внешние меры складываются "неправильно". Предложенное Лебегом определение измеримости, использующее внутреннюю меру, - частный случай условия Каратеодори, в котором A = S. Из-за некоторых специальных свойств внешней меры Лебега это условие оказывается достаточным для модели Лебега, но в общем случае требуется проверять измеримость более детально. Ключевая теорема в теории Каратеодори утверждает, что любая внешняя мера, удовлетворяющая введенным аксиомам, при ограничении только на измеримые множества обладает всеми свойствами, которыми должна обладать мера. Самое важное из этих свойств называется полной аддитивностью. Мера m называется вполне аддитивной, если для любой последовательности E1, E2, E3, ... измеримых множеств, никакие два из которых не имеют общей точки,