або після приведення подібних

, (5)

де , а – кількість слів вигляду в (4), які мають довжину .

Як ми вже казали, всі слова в правій частині (4) різні, отже не перевищує загальної кількості слів двійкового алфавіту довжини :

.

Тоді з (5) випливає

,

або

.

Перейдемо в останній нерівності до границі при . З огляду на те, що одержимо нерівність (3). Теорема доведена.

Наведемо теорему, в деякому сенсі обернену до теореми 2.

Теорема 3. Припустимо, що – набір натуральних чисел, який задовольняє нерівності Макміллана. Тоді існує префіксна схема кодування, для якої – довжини кодових слів.

Доведення. Без втрати загальності можна вважати, що . Серед чисел можуть бути однакові. Якщо виписати всі числа, які зустрічаються в наборі , тільки по одному разу, одержимо інший набір . Знову ж вважаємо, що . Для кожного позначимо через кількість чисел у наборі , які дорівнюють .

Тоді нерівність Макміллана можна переписати у вигляді

.

З цієї нерівності випливає серія допоміжних нерівностей

або ,

або ,

………………………………………………………..

або .

Розглянемо слова двійкового алфавіту, які мають довжину . Їх кількість дорівнює , з огляду на першу з допоміжних нерівностей, серед цих слів можна вибрати різних. Позначимо ці слова через .

Розглянемо множину двійкових слів довжини , які не починаються зі слів . Кількість таких слів дорівнює , з огляду на другу з нерівностей, серед них ми можемо вибрати різних. Введемо для цих слів позначення .

Використовуючи поступово допоміжні нерівності ми одержимо двійкові слова . Якщо взяти їх у якості кодових слів, ми одержимо схему кодування . Ця схема префіксна і

.

Теорема доведена.

З теорем 2 і 3 випливають два дуже цікавих наслідки.

Наслідок 1. Нерівність Макміллана є необхідною і достатньою умовою існування префіксної схеми кодування з довжинами кодових слів .

Наслідок 2. Якщо існує подільна схема кодування з заданними довжинами кодових слів, то існує також префіксна схема кодування з тими ж довжинами кодових слів.

Для доведення цих наслідків слід застосувати спочатку теорему 2, а потім теорему 3.

§3. Оптимальні коди.

Найпростішою подільною схемою кодування є рівномірна схема, в якій усі кодові слова мають однакову довжину. Символи будь-якого алфавіту можна закодувати словами однакової довжини. (Оскільки двійковими словами довжини можна закодувати щонайбільше різних об’єктів, то для рівномірного кодування алфавіту з символів потрібні слова довжини , яка визначається нерівностями .)

Однак на практиці часто зустрічається ситуація, коли одні символи алфавіту вживаються часто, а інші – рідко. Наприклад літера «о» українського алфавіту зустрічається в текстах дуже часто, літера «щ», навпаки, рідко. Тому використовувати для кодування символів алфавіту слова однакової довжини не доцільно. З точки зору економії місця ( пам’яті ЕОМ) вигідно для кодування символів, які зустрічаються в текстах часто, використовувати короткі кодові слова, а для кодування символів, які зустрічаються рідко – довгі. Цей шлях приводить до поняття оптимального коду.

Нехай для символам алфавіту поставлено у відповідність невід’ємні числа , які називаються їх відносними частотами вживання, або просто частотами. При цьому вважаться, що для всіх та

.

На практиці відносні частоти вживання визначаються наступним чином. Береться текст достатньо великого обсягу ( наприклад, деякий літературний твір, якщо йдеться про кодування символів певної природної мови). Для кожного символу за його відносну частоту вживання береться кількість його входжень у даний текст, поділена на довжину всього тексту.

Нехай для даного алфавіту задана схема кодування :

, (6)

( нагадаємо, що ми розглядаємо тільки двійкове кодування, кодові слова складаються з нулів та одиниць). Позначимо через довжини кодових слів . Тоді сума

називається середньою довжиною кодового слова для даної схеми кодування ( і даної системи частот). Якщо на частоти дивитись як на ймовірності появи відповідних символів у тексті то середня довжина кодового слова дорівнює математичному сподіванню довжини кодового слова.

Ясно що схема кодування (6) тим краща, чим менша середня довжина кодового слова . Нехай заданий алфавіт і список частот . Схема кодування (6) для якої середня довжина кодового слова мінімальна називається оптимальною схемою кодування ( для даного списку частот).

За означенням оптимальна схема кодування – це така схема кодування, для якої

, (7)

де точна нижня межа береться за усіма схемами кодування. Але кількість схем кодування нескінчена, отже виникає питання, чи завжди існує оптимальна схема кодування. Відповідь на це питання дає наведена нижче теорема.

Теорема 4. Для будь-якого списку частот оптимальна схема кодування існує.

Доведення. Нехай даний алфавіт зі списком частот . Без втрати загальності можемо вважати, що . Розглянемо рівномірну схему кодування . Довжини кодових слів схеми дорівнюють , де визначене нерівністю . Тоді середня довжина кодового слова дорівнює

.

Отже при обчисленні точної нижньої межі у (7) можна розглядати тільки ті схеми , для яких .

Нехай – схема кодування (6), для якої . Розглянемо довжину кодового слова

.

Отже довжини всіх кодових слів схеми не перевищують числа . Але кількість схем кодування, всі кодові слова яких не за довжиною перевищують константи , скінчена. Це означає, що точну нижню межу у (7) можна брати за скінченою множиною схем кодування. Але у скінченій множині завжди існує мінімальний елемент, отже схема кодування з рівності дійсно існує. Теорема доведена.

У наступному параграфі ми розглянемо конкретний спосіб, як будувати оптимальну схему кодування для даного списку частот. Зараз ми дамо алгоритм який дозволяє будувати схему кодування, хоча й не оптимальну, але близьку до оптимальної.

Для цього розглянемо один дуже корисний спосіб побудови префіксних схем кодування.

Нехай – алфавіт. Розглянемо дерево , яке задовольняє такі умови:

1. всі вершини дерева мають степінь не більший за 3;

2. виділена одна вершина 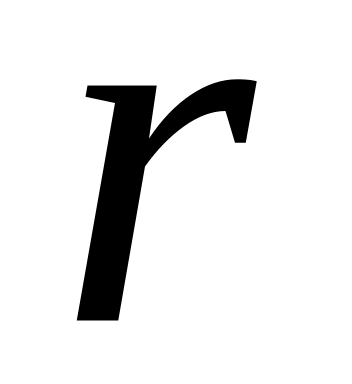дерева, для якої 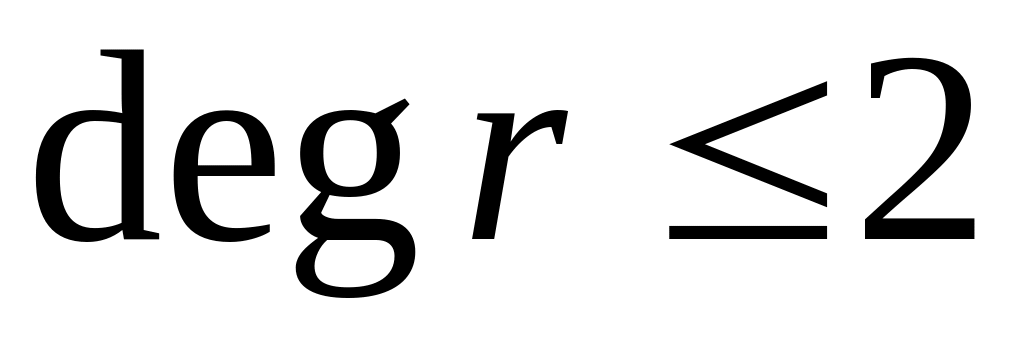, ця вершина називається кореневою вершиною;

3. кожній висячій вершині дерева , відмінній від кореневої, взаємно однозначно поставлена у відповідність деяка літера алфавіту .

Прикладом такого дерева може слугувати дерево на мал. 1.

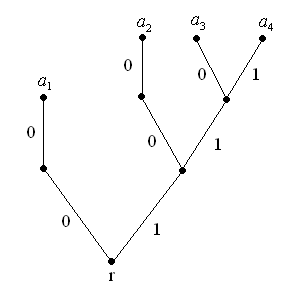
Мал. 1

Будемо казати що, вершина знаходиться на -му ярусі дерева , якщо відстань від кореневої вершини до вершини дорівнює . Якщо вершина лежить на -му ярусі, а вершина лежить на -му ярусі дерева , причому , то кажуть, що вершина лежить на вищому ярусі за вершину .

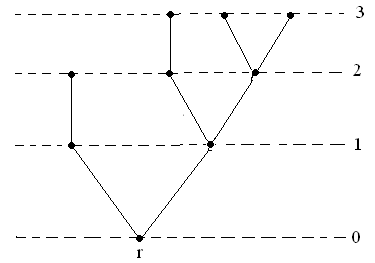
Мал. 2

Мал. 2 ілюструє розбиття множини вершин дерева на яруси. Очевидно на нульовому ярусі лежить тільки коренева вершина.

Всі висячи вершини відмінні від кореневої (остання може бути, а може не бути висячою) називаються кінцевими вершинами дерева . Кожна вершина, яка не є кінцевою суміжна або з однією або з двома вершинами, які лежать на вищому ярусі. Припишемо кожному ребру дерева символ двійкового алфавіту (нуль або одиницю), так щоб кожним двом ребрам, які з’єднують будь-яку не кінцеву вершину з вершинами, які лежать на вищому ярусі, відповідають різні символи ( мал. 1).

Нехай – символ алфавіту . Рухаючись від кореневої вершини до кінцевої вершини, яка зображує символ , і виписуючи всі двійкові символи приписані ребрам, які ми проходимо на цьому шляху, одержимо двійкове слово . Отже поставивши подібним чином двійкове слово кожному символу алфавіту ми одержимо схему кодування . Очевидно ця схема кодування префіксна. Дерево називається кодовим деревом одержаної схеми кодування .

Наприклад схема кодування, яка відповідає кодовому дереву на мал. 1 має вигляд:

.

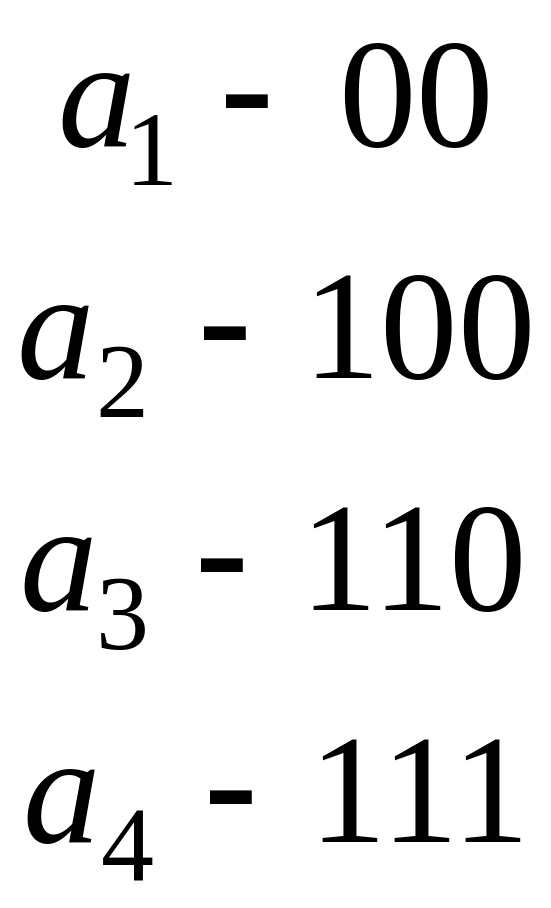Навпаки, кожній префіксній схемі кодування відповідає деяке кодове дерево.

Розглянемо алгоритм, який дозволяє побудувати близький до оптимального код, який називається кодом Фано.

Нехай даний алфавіт зі списком частот , причому . Ділимо алфавіт на дві групи символів та , так щоб суми частот в цих групах були якомога ближчими одна до одної. Першій групі приписуємо символ 0, другій групі – символ 1. Після цього вчиняємо аналогічно з кожною з одержаних груп і так далі, допоки всі групи не міститимуть рівно по одному символу. Після цього код кожного символу можна одержати, виписуючи всі нулі та одиниці, приписані всім групам у яких зустрівся даний символ у тому порядку, в якому ці групи з’являлися в процесі виконання алгоритму.

Процес побудови коду Фано зручно проводити, будуючи його кодове дерево.

Задача 1. Побудувати код Фано для символів із заданими частотами , , , .

Розв’язання. Розіб’ємо всі символи алфавіту на дві групи – в першій буде один символ , у другій символи ( мал. 3). Другу групу розбиваємо на групи та . Нарешті останню групу розбиваємо на дві групи по одному символу в

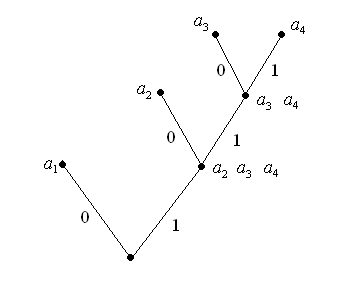
Мал. 3

кожній. Одержуємо схему кодування :

.

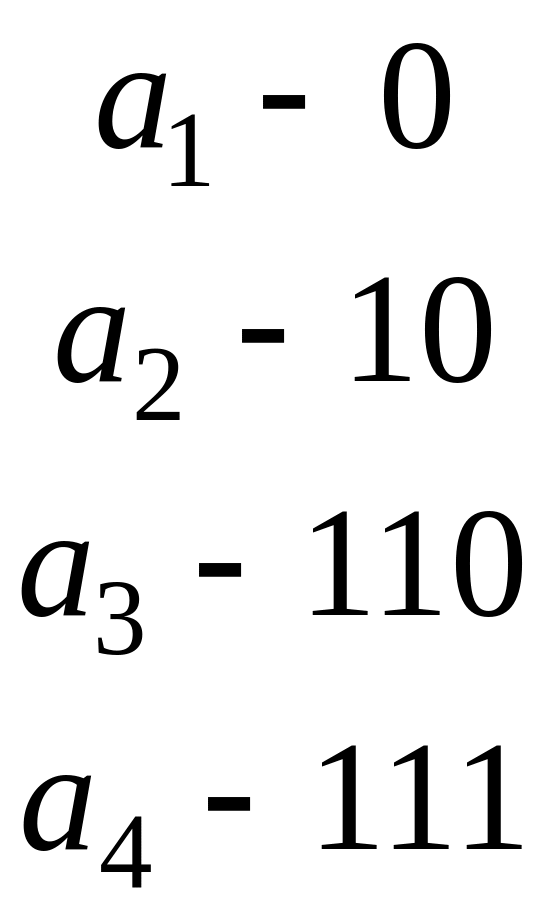Підрахуємо середню довжину кодового слова цієї схеми кодування.

.