§4. Код Хаффмана.

В цьому параграфі ми розглянемо алгоритм побудови оптимального коду. Схема кодування, яка будується з допомогою цього алгоритму називається кодом Хаффмана. Побудова коду Хаффмана складається з виконання над алфавітом із заданими частотами двох операцій – стиснень та розщеплень.

Нехай заданий алфавіт зі списком частот , причому частоти впорядковані за незростанням: . Процес стиснення полягає в заміні двох символів з найменшими частотами на один символ , якому приписується частота .

Після стиснення ми одержуємо новий алфавіт зі списком частот . Нехай для цього алфавіту побудована схема кодування :

.

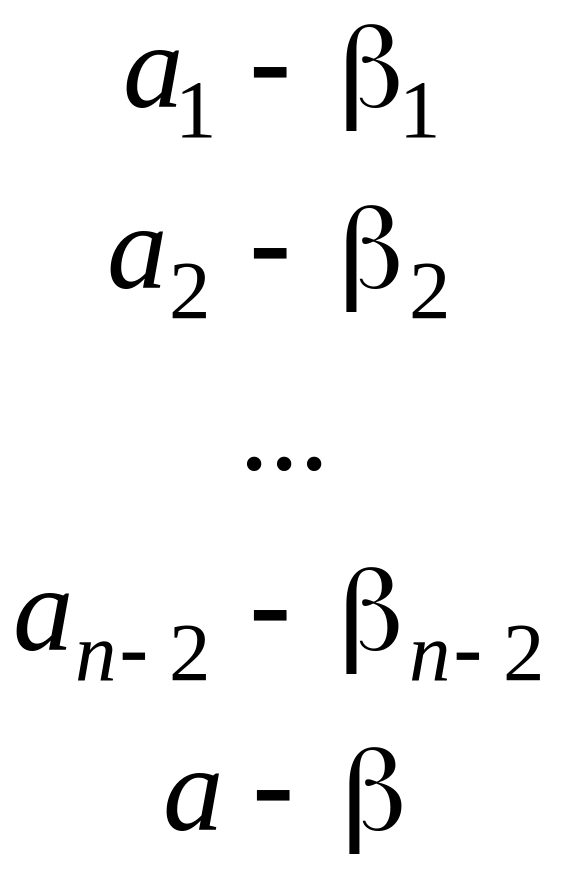На основі схеми будуємо схему кодування символів алфавіту . Символам схема ставить у відповідність ті ж самі кодові слова, що й схема . Символам ставиться у відповідність, слово, яке кодує символ з приписаним до нього праворуч нулем у випадку символу і одиницею у випадку символу . Отже схема має вигляд:

.

Операція одержання схеми зі схеми називається розщепленням, ця операція обернена до операції стиснення. Нижче буде доведено, що якщо схема – оптимальна для списку частот , то – оптимальна для списку частот .

Опишемо тепер алгоритм одержання коду Хаффмана. Нехай заданий алфавіт зі списком частот , впорядкованим за незростанням: . Шляхом стиснення алфавіту одержуємо новий алфавіт з частотами . Розташовуємо символи алфавіту в порядку незростання частот і знову застосовуємо процедуру стиснення (для того щоб виконати стиснення необхідно, щоб алфавіт був впорядкований за незростанням частот). Повторюємо цю процедуру, поки не одержимо алфавіт з двох символів. Для алфавіту з двох символів нескладно побудувати оптимальну схему кодування – перший символ кодуємо нулем, другий символ – одиницею. Після цього, шляхом послідовних розщеплень одержуємо оптимальну схему кодування для списку частот .

Краще за все виконувати процес побудови коду Хаффмана графічно. Розглянемо це на прикладі задачі.

Задача 2. Побудувати код Хаффмана для символів із частотами: , , , , .

Розв’язання. Випишемо всі частоти в стовпчик у порядку незростання (третій стовпчик зліва на схемі, зображеній на мал. 4). Після цього виконуємо над ними опе-

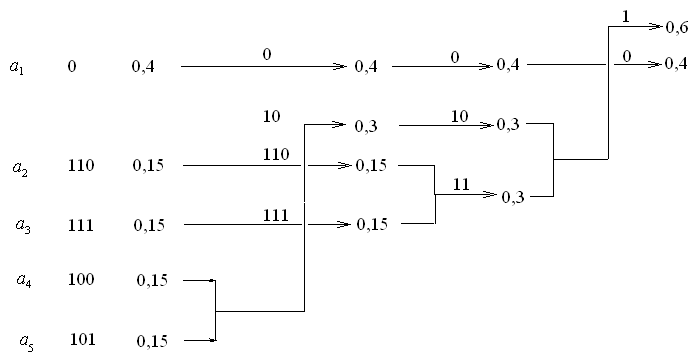
Мал. 4

рацію стиснення. Одержані частоти знову виписуємо в стовпчик у порядку незростання ( 0,4; 0,3; 0,15; 0,15). Стиснення зображені на схемі стрілочками. Продовжуємо цей процес, доки не одержимо дві частоти. Після цього виконуємо обернені до цих стиснень розщеплення, на кожному етапі одержані кодові слова записуємо ліворуч від відповідних частот. Після останнього розщеплення одержуємо код Хаффмана:

.

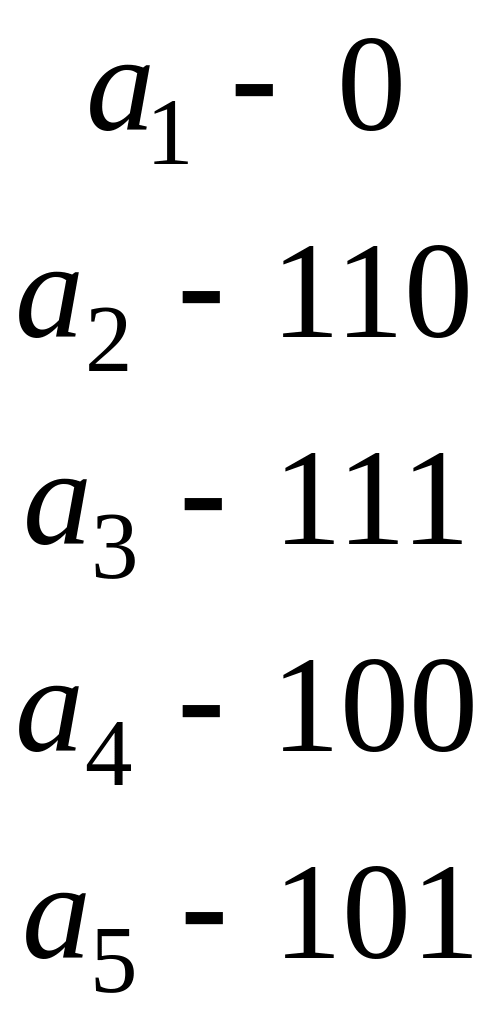Підрахуємо середню довжину кодового слова коду Хаффмана для даного списку частот:

.

В той час, якби ми користувалися рівномірним кодом, всі кодові слова мали б довжину 3 і середня довжина кодового слова теж би була рівною 3. З означення оптимального коду випливає, що кращої економії місця для даного списку частот за допомогою алфавітного кодування домогтися неможливо.

Розглянемо ще один приклад побудови коди Хаффмана.

Задача 3. Побудувати код Хаффмана для символів із частотами: , , , .

Розв’язання. Так само, як і при розв’язанні попередньої задачі будуємо схему (мал. 5).

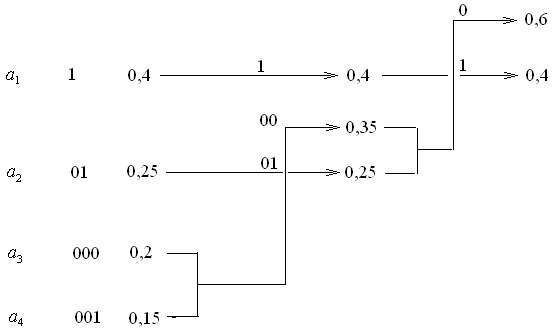
Мал. 5

Зі схеми одержуємо код Хаффмана :

.

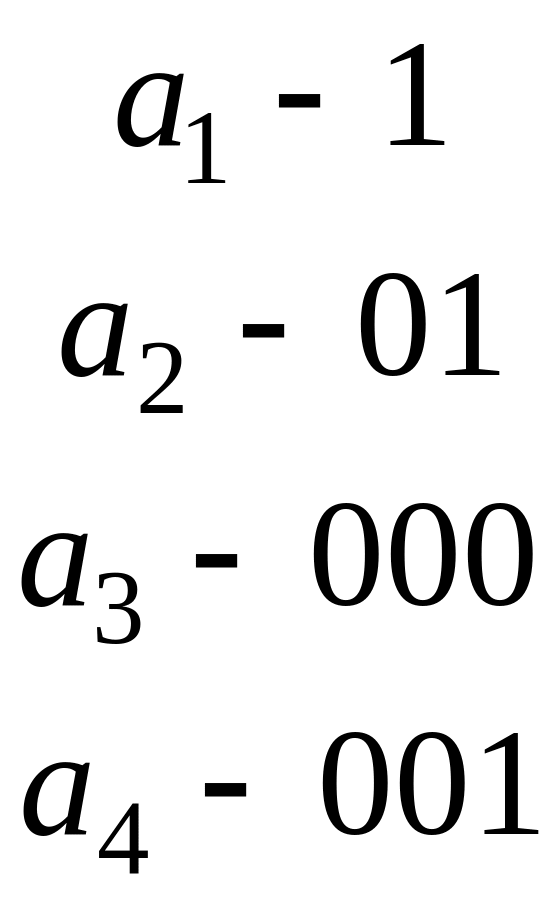Середня довжина кодового слова дорівнює

.

Зазначимо, що середня довжина кодового слова коду Хаффмана для даного списку частот збігається з середньою довжиною кодового слова коду Фано (див. задача 1). Отже код Фано для даного списку частот також є оптимальним.

Перейдемо до обґрунтування алгоритму побудови оптимального коду.

Для цього нам знадобляться такі три леми.

Лема 1. Нехай – оптимальна схема кодування для списку частот і – довжини кодових слів. Тоді якщо для деяких , то .

Доведення. Припустимо супротивне – що Побудуємо нову схему кодування , помінявши у схемі місцями кодові слова . Тобто має вигляд

.

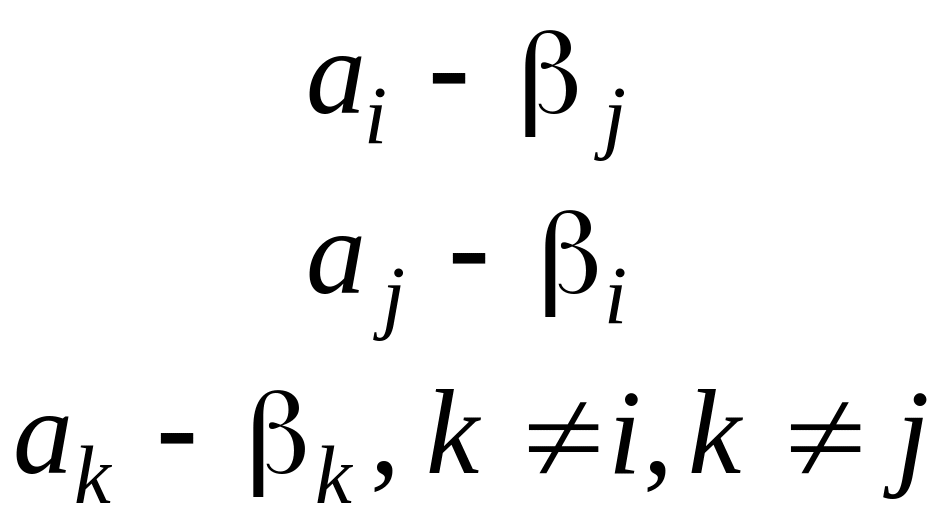Підрахуємо середні довжини кодових слів схем :

,

.

При підрахуванні різниці сума знищиться і ми одержимо

,

за умовою леми і припущенням . Отже , що суперечить оптимальності схеми . Лема доведена.

Лема 2. В кодовому дереві оптимального коду кожна вершина, яка не є кореневою і не є висячою має степінь 3.

Доведення. Припустимо супротивне – в кодовому дереві оптимальної схеми кодування існує вершина степеня 2, яка не є кореневою (мал. 6). Видалимо з кодового дерева одне з ребер, інцідентних цій вершині. При цьому довжини деяких кодових слів зменшаться, а довжини всіх інших кодових слів не зміняться. Тоді середня довжина кодового слова теж зменшиться. Отже новому дереву відповідає нова схема з меншою за середньою довжиною кодового слова. Це суперечить оптимальності схеми кодування . Лема доведена.

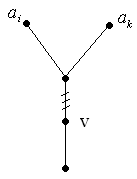
Мал. 6

Лема 3. Серед оптимальних схем кодування для списку частот , існує така, що у відповідному їй кодовому дереві вершини, які зображують символи , суміжні одній вершині (мал. 7).

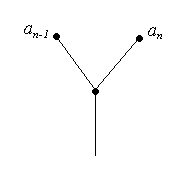
Мал. 7

Доведення. Нехай – оптимальна схема кодування. З леми 1 випливає, що ми завжди можемо так перенумерувати частоти та відповідні їм кодові слова, що

. (8)

Дійсно, якщо , то з леми 1 випливає, що . Якщо , але то ми можемо поміняти місцями частоти та відповідні ним кодові слова. Повторюючи цю процедуру необхідне число разів ми одержимо потрібну нам нумерацію.

Нехай – вершина, суміжна вершині . – кодове слово яке має найбільшу довжину, отже вершина знаходиться на найвищому ярусі. За лемою 2 вершина має степінь 3, отже вона суміжна ще одній вершині (мал. 8). Якщо , то лема доведена. Якщо , то це означає, що . Тоді ми

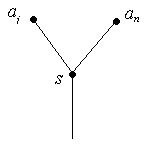
Мал. 8

можемо поміняти місцями символи та (і відповідні ним кодові слова). Середня довжина кодового слова від цього не зміниться. Отже нова, одержана нами схема кодування теж буде оптимальною. Лема доведена.

Лему 3 можна переформулювати іншим чином: серед оптимальних схем кодування існує така, що кодові слова з найменшими частотами відрізняються тільки в останньому символі.

Розглянемо алфавіт , який складається з символів з частотами , причому . Нехай –схема кодування

,

в якій довжини не менші за довжини інших кодових слів, а самі слова відрізняються лише в останньому символі: , . Розглянемо новий алфавіт зі списком частот і нову схему кодування :

.

Теорема 5. Якщо – оптимальна схема кодування для списку частот , то – оптимальна схема кодування для списку частот .

Доведення. З’ясуємо спочатку як пов’язані між собою середні довжини кодових слів та . Позначимо, як і раніше, через довжину кодового слова . Тоді

і оскільки , то

.

Отже ми встановили рівність

. (9)

Припустимо, тепер, що – оптимальна схема кодування для списку частот , але – не оптимальна схема кодування для частот . Позначимо через оптимальну схему кодування для частот , очевидно що . Схема кодування має вигляд

.

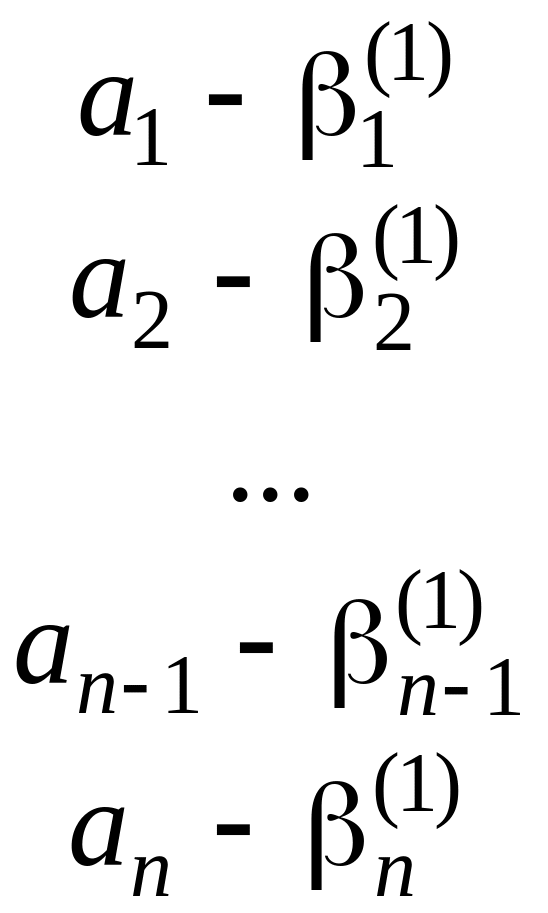З огляду на лему 3 ми можемо вважати, що не менші за довжини інших кодових слів, а самі слова відрізняються лише в останньому символі. Тоді ми можемо побудувати схему кодування для списку частот , таку що

. (10)

З рівностей (9), (10) та нерівності випливає, що

.

Ми одержали, що і схема кодування не є оптимальною для списку частот , що суперечить умові теореми. Теорема доведена.

З теореми 5 випливає, що код Хаффмана дійсно є оптимальним кодом для будь-якого списку частот.