
Лабораторная Работа № 2
''Метод прямоугольника.''
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0.
Если
отрезок ![]() является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по
является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по
Формуле левых прямоугольников:
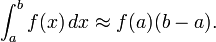
Формуле правых прямоугольников:

Формуле прямоугольников (средних):

Лабораторная Работа № 2
Функция: f(x) = sin(x) – 0,2x
Программа для вычисления, путем "метода прямоугольника"
CLS
PRINT " INTEGRIROVANIE METODOM PRAMOYGOLNIKA "
INPUT "VV INTERVAL A,В"; A1, B1: A = A1: B = B1
INPUT "VV N"; N1: N = N1: I = 0: S1 = 0
DEF FNF (X) = (X^ 2) * SIN(X)
X1 = (B - A) / N: PRINT "X=(B-A)/N="; X1
FOR X = A to B + X1 STEP X1
Y = FNF (X): PRINT "X"; I; "="; X, "Y"; I; "="; Y
I = I + 1
S1 = S1 + Y
NEXT X
INPUT "VV NACH ILI KON INTERVAL "; Z1: Z = Z1
S = X1 * (S1 - FNF(Z))
PRINT "S="; S
END
вывод программы:
Integrirovanie metodom praymoygolnika Integrirovanie metodom praymoygolnika Интервал (A,B) = (0, 1) Интервал (A,B) = (0, 1) N = 100 N = 200
S= 0.2276936 S= 0.2254079
Лабораторная работа № 3
''Метод простых итераций решения уравнения F(x) = 0''
Метод
простых итераций ( метод последовательных
приближений) решения уравнения F(x)
= 0 состоит в замене исходного уравнения
эквивалентным ему уравнением x
= ϕ( )
и построении последовательности
)
и построении последовательности
 ϕ(
),
сходящейся при n→∞
к точному значению решению Ḝ. Сформулируем
достаточное условие сходимости метода
простых итераций.
ϕ(
),
сходящейся при n→∞
к точному значению решению Ḝ. Сформулируем
достаточное условие сходимости метода
простых итераций.
Теорема.
Пусть функция ϕ(
)
определена и дифференцируема на [a,b],
причем все ее значения ϕ(
)
є [a,b].
Тогда, если существует число q,
такое, чтo
 на отрезке [a,b],
то последовательность
на отрезке [a,b],
то последовательность
 сходится к единственному на [a,b]
решению уравнения x
= ϕ(x)
при любом значении
сходится к единственному на [a,b]
решению уравнения x
= ϕ(x)
при любом значении
 т.е
т.е

При
этом, если на отрезке
 производная
производная
 ,
то |
,
то | ,
если
,
если
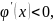 то
|
то
|
Опишем
один шаг итераций. Исходя из найденного
на предыдущем шаге значения
 ,
вычисляем y
= ϕ(
).
Если |y
-
,
вычисляем y
= ϕ(
).
Если |y
-
 ,
полагают
,
полагают
 и
выполняют очередную итерацию. Если|y
-
,
то вычисления заканчиваются и за
приближенное значение корня принимают
величину
.
Погрешность полученного результата
зависит от знака производной
и
выполняют очередную итерацию. Если|y
-
,
то вычисления заканчиваются и за
приближенное значение корня принимают
величину
.
Погрешность полученного результата
зависит от знака производной
 .
При
корень найден с погрешностью
.
При
корень найден с погрешностью
 ,
если
,
если
 ,
то погрешность не превышает ξ
,
то погрешность не превышает ξ
Метод
допускает простую геометрическую
интерпретацию. Построить графики функций
y=x
и y= .
.
